Newton’s second law of motion, also known as the law of force, is a fundamental principle in physics that describes the behavior of objects when forces are unbalanced. This law, formulated by Sir Isaac Newton, provides crucial insights into how objects accelerate and move in response to external forces. Understanding Newton’s second law is essential for comprehending the principles of motion and the calculations involved in determining the effects of forces on objects. In this article, we will explore the key aspects of Newton’s second law of motion, including its definition, derivation, applications, and solved examples.
What is Newton’s Second Law Of Motion?
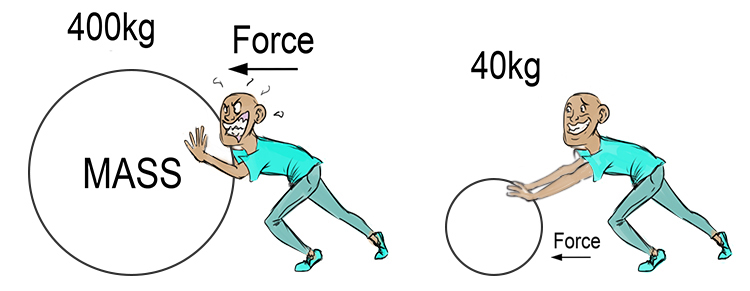
Newton’s second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In simpler terms, the greater the force applied to an object, the greater its acceleration will be. Conversely, if the mass of an object increases, its acceleration decreases for the same applied force. This law can be mathematically expressed as:
[F = ma]
Where:
- (F) represents the net force acting on the object,
- (m) denotes the mass of the object, and
- (a) signifies the acceleration produced by the net force.
This equation reveals that force and acceleration are directly proportional, while force and mass are inversely proportional. It implies that a larger force will result in a greater acceleration, whereas a larger mass will lead to a smaller acceleration for the same force.
Who is Newton?
Before delving further into Newton’s second law, it is essential to understand the background and contributions of Sir Isaac Newton. Born on December 25, 1642, in Woolsthorpe, England, Newton was a mathematician, physicist, and astronomer. He made significant advancements in various scientific fields, including mathematics, optics, and mechanics. His most famous work, “Philosophiæ Naturalis Principia Mathematica,” published in 1687, laid the groundwork for classical mechanics and introduced his three laws of motion.
Newton’s laws of motion were groundbreaking, as they provided a comprehensive explanation of how objects move and interact with forces. These laws became the foundation of classical mechanics, revolutionizing the study of physics and shaping our understanding of the physical world.

Newton’s Second Law: Force
Newton’s second law of motion is primarily concerned with the relationship between force, mass, and acceleration. It states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In other words, an object will only accelerate if there is an unbalanced force acting upon it. The presence of an unbalanced force results in changes in an object’s speed, direction, or both.
The second law can be expressed in equation form as:
[F = ma]
This equation demonstrates that the net force acting on an object is equal to the product of its mass and acceleration. The direction of the net force is the same as the direction of the acceleration. Therefore, if a force is applied to an object in a specific direction, the object will accelerate in that direction.
It is important to note that force is a vector quantity, meaning it has both magnitude and direction. The same applies to acceleration, which is also a vector. This implies that the direction of the net force and the resulting acceleration will be the same.
For those exploring the principles of Newton’s second law of motion, our Newton’s first law of motion and Newton’s third law of motion pages serve as insightful companions. Together, they provide a comprehensive understanding of Newton’s laws, elucidating the relationships between force, motion, and the fundamental principles that govern physical interactions in the world of classical mechanics.
Newton’s Second Law Formula
The mathematical representation of Newton’s second law is usually written as F = ma, where F represents the total force acting on the object, m stands for the mass of the object, and a denotes the acceleration.
Deriving Newton’s Second Law
For Changing Mass
Consider a scenario where an object’s mass changes over time, like a rocket propelling in space. The force exerted on the object can be expressed as F = (m1v1 - m0v0) / (t1 - t0), where m0 and v0 represent the initial mass and velocity, and m1 and v1 represent the final mass and velocity.
For Constant Mass
In most circumstances, the mass of an object remains constant. In such a case, the force can be represented as F = m * (v1 - v0) / (t1 - t0). This formula simplifies to F = ma, a more familiar form of Newton’s second law.
Application of Second Law
Pushing a Cart
The concept of Newton’s second law can be seen when pushing a shopping cart. A heavier cart requires more force to move and accelerates slower than a lighter one.

Kicking a Ball
When a football player kicks a ball, the force exerted determines how far and fast the ball will travel. A stronger kick (more force) will send the ball farther (more acceleration).

Two People Walking
Among two people walking, if one is heavier than the other, the one weighing heavier will walk slower because the acceleration of the person weighing lighter is greater.

Newton’s Second Law Examples
Uniformly Accelerated Motion
A car accelerating uniformly on a straight road is an example of Newton’s second law. The force exerted by the car engine results in the car’s acceleration.
Uniform Circular Motion
When an object moves in a circular path at a constant speed, it experiences an acceleration towards the center of the circle. This centripetal acceleration is caused by a net force directed towards the center.
Harmonic Motion
A swinging pendulum is a classic example of harmonic motion. The restoring force acting on the pendulum is proportional to its displacement, resulting in its back-and-forth oscillation.
Objects with Variable Mass
A rocket ascending in space is an excellent example of an object with variable mass. As the rocket burns fuel, its mass decreases, leading to an increase in its acceleration.
Chaos and Unpredictability
While Newton’s second law provides a fundamental understanding of how forces affect objects, it is important to note that certain systems can exhibit chaotic behavior, making predictions challenging. Chaotic systems are sensitive to small changes in initial conditions, leading to unpredictable outcomes.
One example of chaotic behavior is the famous “butterfly effect,” where a small change in initial conditions can lead to significantly different outcomes over time. This phenomenon highlights the limitations of deterministic predictions when dealing with complex systems.
Therefore, although Newton’s second law provides a powerful tool for understanding the relationship between force, mass, and acceleration, it is crucial to consider the potential for chaos and unpredictability in certain scenarios.
Relation to Other Formulations of Classical Physics
Newton’s second law of motion is a fundamental principle in classical physics and serves as a cornerstone for various other formulations and theories. It provides the foundation for classical mechanics, which describes the motion of macroscopic objects.
Newton’s second law is closely related to other important principles in physics, such as conservation of momentum and energy. Momentum, defined as the product of an object’s mass and velocity, is directly related to force and acceleration through Newton’s second law. Energy, another fundamental concept, is also linked to force and acceleration, as the work done on an object is equal to the force applied multiplied by the distance traveled.
By understanding the relationships between these concepts, scientists and engineers can analyze and predict the behavior of objects in a wide range of physical phenomena.
How does Newton’s Second Law of Motion Apply to Rockets?
Newton’s second law of motion is particularly relevant to rockets and the field of rocket science. According to this law, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This principle applies to rockets in two significant ways.
Firstly, the force experienced by a rocket is equal to the rate of change of momentum. As the rocket expels gases or propellant, the mass of the rocket decreases over time. According to Newton’s second law, this decrease in mass leads to an increase in acceleration, allowing the rocket to propel itself forward.
Secondly, rockets operate on the principle of action and reaction, as defined by Newton’s third law of motion. For every action force exerted by the rocket (expulsion of gases), an equal and opposite reaction force is exerted on the rocket itself. This reaction force propels the rocket forward, enabling it to achieve the desired velocity and trajectory.
Newton’s second law of motion plays a crucial role in the design and operation of rockets, allowing engineers to calculate the forces and accelerations involved in space exploration and satellite launches.
How do We Use Newton’s Second Law?
Newton’s second law of motion is a fundamental principle used in various fields of science and engineering. Its applications extend beyond theoretical understanding and are widely used in practical calculations and problem-solving.
In engineering and physics, Newton’s second law is employed to determine the forces and accelerations acting on objects. By knowing the mass of the object and the net force applied, engineers can calculate the resulting acceleration or determine the force required to achieve a desired acceleration.
For example, in automotive engineering, Newton’s second law is used to optimize the performance and safety of vehicles. By considering the forces acting on a car, engineers can design systems such as brakes, suspensions, and engines to ensure optimal acceleration and handling.
In sports, Newton’s second law is relevant to understanding the motion and forces involved in various activities. Whether it’s analyzing the forces exerted during a baseball pitch or calculating the acceleration of a sprinter, knowledge of Newton’s second law allows coaches and athletes to optimize performance and technique.
Overall, Newton’s second law serves as a fundamental tool for analyzing and predicting the behavior of objects in a wide range of practical applications.
What do We do hen a Force is Directed at an Angle?
In some situations, forces may act on an object at an angle rather than in a straight line. When a force is directed at an angle, it can be resolved into two components: one parallel to the direction of motion and one perpendicular to it.
To analyze the effects of a force at an angle, we can use trigonometry to determine the magnitudes of the parallel and perpendicular components. Once these components are known, we can apply Newton’s second law separately to each component.
For example, consider a block being pulled up an inclined plane by a rope. The force exerted by the rope can be resolved into a component parallel to the plane and a component perpendicular to the plane. The parallel component contributes to the acceleration of the block along the plane, while the perpendicular component affects the normal force and gravitational force acting on the block.
By breaking down the force into its components and applying Newton’s second law to each component separately, we can analyze the motion and forces involved in situations where forces act at angles.
How does Newton’s Second Law Apply to a Car Crash?
Newton’s second law of motion also applies to understanding the forces involved in car crashes. When a car collides with another object or experiences a sudden change in velocity, the forces exerted on the car can have significant consequences.
According to Newton’s second law, the force experienced by an object is directly proportional to its mass and acceleration. In the case of a car crash, the force exerted on the car depends on the change in velocity and the duration of the collision.
During a crash, the car experiences a rapid deceleration or acceleration, depending on the direction of the collision. This change in velocity results in a large net force acting on the car, potentially causing damage to the vehicle and its occupants.
Understanding the principles of Newton’s second law allows engineers and safety experts to design and implement measures to mitigate the forces experienced during car crashes. By considering the impact of forces on the structure of the car and the safety features such as seatbelts and airbags, engineers can enhance occupant safety and minimize the potential for injuries.
Daily Life Examples of Newton’s Second Law Of Motion
Newton’s second law of motion is evident in numerous aspects of our daily lives. Here are some examples that illustrate how this law applies to everyday situations:
- Riding a bicycle: When pedaling a bicycle, the force exerted on the pedals results in acceleration. The harder you push on the pedals, the greater the force, and the faster you accelerate.
- Swinging on a swing: When you swing on a playground swing, the force exerted by your legs and body propels you forward and upward. The larger the force, the greater the acceleration and the higher you swing.
- Throwing a ball: When throwing a ball, the force applied to the ball determines its acceleration and trajectory. A stronger throw results in a greater force, leading to a faster and longer throw.
- Braking a car: When applying the brakes in a car, the force exerted on the brake pedal results in deceleration. The greater the force applied, the faster the car slows down.
These examples demonstrate how Newton’s second law of motion is present in our daily activities, influencing the way objects move and accelerate.

The Direction of the Net Force and Acceleration
As stated earlier, Newton’s second law of motion indicates that the direction of the net force is the same as the direction of the resulting acceleration. This relationship is crucial in understanding the motion of objects and the effects of forces.
When a force is applied to an object, it causes a change in its velocity, resulting in acceleration. The direction of this acceleration is determined by the direction of the net force. If the force acts in the same direction as the object’s initial motion, it accelerates the object further in that direction. Conversely, if the force acts opposite to the object’s initial motion, it decelerates the object or changes its direction.
For example, if you push a book on a table with a force directed to the right, the book accelerates to the right. The net force acting on the book is in the same direction as its resulting acceleration. Similarly, if you apply a force to the left, the book decelerates or changes its direction, depending on the magnitude of the force.
Understanding the relationship between the net force and acceleration enables us to predict and analyze the motion of objects in different scenarios.
Newton’s Second Law Of Motion Statement
In summary, Newton’s second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This law provides a fundamental understanding of how forces affect objects and allows us to calculate the resulting acceleration or the force required to achieve a desired acceleration.
By applying Newton’s second law, we can analyze and predict the behavior of objects in various scenarios, whether it’s the motion of a car, the flight of a rocket, or the behavior of objects in everyday life. This law serves as the foundation for classical mechanics and plays a significant role in physics, engineering, and other scientific fields.
Solved Examples of Newton’s Second Law Of Motion (Force)
To further illustrate the practical application of Newton’s second law, let’s explore some solved examples:
Example 1: Calculating Acceleration
If we have a block with a mass of 2 kg and a net force of 20 N acting on it in the positive x-direction, what would be its acceleration?
First, we need to calculate the net force acting on the block:
F = 20 N
Then, we can use Newton’s second law to find the acceleration:
20 / 2 = 10
Therefore, the block will experience an acceleration of 10 m/s² in the positive x-direction.
Example 2: Determining Net Force
How much horizontal net force is required to accelerate a 1000 kg car at 4 m/s²?
To find the net force, we can rearrange Newton’s second law equation:
F = 1000 ,
1000 * 4 = 4000
Therefore, a net force of 4000 N is required to accelerate the 1000 kg car at 4 m/s².
These examples illustrate how Newton’s second law can be applied to solve problems involving forces, mass, and acceleration. By understanding this law and its formulas, we can analyze and calculate the effects of forces on objects in various scenarios.
How Kunduz Can Help You Learn Solved Examples of Newton’s Second Law Of Motion (Force)?
Kunduz is an online learning platform dedicated to providing comprehensive educational resources to students. Whether you’re studying physics, mathematics, or any other subject, Kunduz offers a range of materials and tools to support your learning.
When it comes to understanding and solving examples related to Newton’s second law of motion, Kunduz provides step-by-step explanations and practice problems. With detailed solutions and clear explanations, you can enhance your understanding of this fundamental law and apply it to various situations.
Kunduz’s interactive learning resources, including videos, quizzes, and practice exercises, enable you to engage with the material and reinforce your knowledge. By utilizing Kunduz’s educational resources, you can confidently tackle solved examples of Newton’s second law of motion and develop a strong foundation in physics.
In conclusion, Newton’s second law of motion is a fundamental principle that describes the relationship between force, mass, and acceleration. By understanding and applying this law, we can analyze the effects of forces on objects and calculate their resulting accelerations. Newton’s second law finds application in numerous real-life scenarios, from car crashes to rocket launches. With Kunduz’s educational resources, you can enhance your understanding and solve examples related to Newton’s second law of motion effectively.
