In the field of geometry, angles play a crucial role in understanding the relationships between lines, shapes, and measurements. One important type of angle is the obtuse angle. In this article, we will delve into the definition, properties, construction, and applications of obtuse angles.
What is an Angle?
Before we dive into the specifics of obtuse angles, let’s first understand what an angle is. In geometry, an angle is formed when two rays share a common endpoint called the vertex. The rays that form the angle are known as the sides of the angle.

What is the Obtuse Angle?
An obtuse angle is a type of angle that measures greater than 90 degrees but less than 180 degrees. In other words, it is an angle that is larger than a right angle (90 degrees) but smaller than a straight angle (180 degrees).
Obtuse Angle Degree
The degree measure of an obtuse angle falls within the range of 90 degrees to 180 degrees. Some examples of obtuse angle degrees include 110°, 135°, 150°, and 179°. It is important to note that all angles within this range are considered obtuse angles.
Obtuse Angle Formula
To determine if an angle is obtuse, you can use the following formula:
Angle > 90° and Angle < 180°
If the angle satisfies this condition, it can be classified as an obtuse angle.
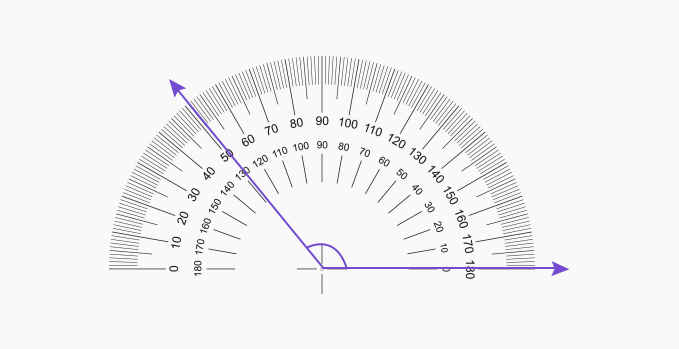
How to Construct an Obtuse Angle?
Constructing an obtuse angle can be done using a protractor or a compass. Let’s explore both methods.
Constructing an Obtuse Angle with a Protractor
To construct an obtuse angle using a protractor, follow these steps:
- Draw a straight line using a ruler.
- Place the center of the protractor at one end of the line.
- Count from zero and mark a dot at the desired obtuse angle measurement.
- Remove the protractor and use a ruler to join the end of the line to the marked dot.
- Mark the angle and double-check its accuracy using the protractor.

Constructing an Obtuse Angle with a Compass
To construct an obtuse angle using a compass, follow these steps:
- Draw a ray (line segment with one endpoint).
- Place the compass at the endpoint of the ray and draw an arc that intersects the ray.
- Without changing the compass width, place the compass at the point where the arc intersects the ray and draw another arc.
- Draw a line segment connecting the endpoint of the ray to the point where the second arc intersects the ray.
- The resulting angle is the desired obtuse angle.

Obtuse Angle Triangle
An obtuse angle triangle is a type of triangle where one of its angles measures greater than 90 degrees. In an obtuse angle triangle, the sum of the three interior angles is always 180 degrees. It is important to note that an obtuse angle triangle can be either isosceles or scalene, but it cannot be equilateral.

Properties of Obtuse Angle
Here are some important properties of obtuse angles:
- An obtuse angle measures greater than 90 degrees but less than 180 degrees.
- The side opposite the obtuse angle in a triangle is the longest side.
- In an obtuse triangle, the sum of the squares of the two shorter sides is less than the square of the longest side.
- When one angle of a triangle is obtuse, the other two angles are always acute.
Types of Obtuse Angle
Obtuse angles can be found in various shapes and figures. Let’s explore some common examples:
Obtuse Angle of a Triangle
In a triangle, if one of the angles measures greater than 90 degrees, it is classified as an obtuse angle triangle. This means that one angle in the triangle is obtuse, while the other two angles are acute.
Obtuse Angle of a Rhombus
A rhombus is a quadrilateral with all sides of equal length. In a rhombus, two opposite angles are obtuse, while the other two opposite angles are acute.
Obtuse Angle of a Parallelogram
In a parallelogram, opposite angles are congruent. This means that if one angle is obtuse, the opposite angle will also be obtuse.
Obtuse Angle vs. Acute Angle
Let’s compare and contrast obtuse angles and acute angles:
| Obtuse Angle | Acute Angle |
|---|---|
| Measures greater than 90° and less than 180° | Measures less than 90° |
| One angle in a triangle can be obtuse | All angles in a triangle are acute |
| Side opposite to the obtuse angle is the longest side in a triangle | No side is specifically related to acute angles |
| Can be found in various shapes and figures | Commonly found in triangles and other small shapes |
Types of Angles
Apart from obtuse angles, there are several other types of angles that are commonly encountered in geometry. Let’s explore some of them:
Acute Angle
An acute angle is an angle that measures less than 90 degrees. It is smaller than both a right angle and an obtuse angle.
Right Angle
A right angle measures exactly 90 degrees. It is commonly found in squares, rectangles, and other shapes with perpendicular sides.
Straight Angle
A straight angle is a flat angle that measures exactly 180 degrees. It forms a straight line and is commonly encountered in geometric proofs and transformations.
Reflex Angle
A reflex angle measures more than 180 degrees but less than 360 degrees. It is formed when two rays rotate beyond a straight angle.
Full Angle
A full angle is an angle that measures exactly 360 degrees. It represents a complete rotation.
Frequently Asked Questions on Obtuse Angle
How to Determine If a Triangle is Obtuse?
If you know the measures of two angles of a triangle, you can find the third angle using the angle sum property of a triangle. If the third angle is greater than 90 degrees, the triangle is obtuse. If you only know the lengths of the sides of the triangle, you can use the Pythagorean inequality to determine if the triangle is obtuse.
What does an Obtuse Angle look like?
An obtuse angle measures more than 90 degrees but less than 180 degrees. It looks like an angle that has been opened wider than a right angle.
What Are the Characteristics of an Obtuse-Angled Triangle?
An obtuse-angled triangle has one angle that measures more than 90 degrees. The side opposite the obtuse angle is the longest side of the triangle.
Can 2 Obtuse Angles be Supplementary and what are the zero angles?
No, two obtuse angles cannot be supplementary because their sum would be more than 180 degrees. A zero angle is an angle that measures exactly 0 degrees.
What is the definition of 210 degrees and give an example of an obtuse angle?
210 degrees is a reflex angle because it measures more than 180 degrees. An example of an obtuse angle can be 120 degrees, which measures more than 90 degrees but less than 180 degrees.
What is the difference between acute angle and obtuse angle?
An acute angle measures less than 90 degrees, whereas an obtuse angle measures more than 90 degrees but less than 180 degrees.
How many degrees does an obtuse angle have?
An obtuse angle measures more than 90 degrees but less than 180 degrees.
Solved Examples on Obtuse Angle
Let’s solve a few examples to further illustrate the concept of obtuse angles.
Example 1: Determine the value of x in the given triangle ABC.
Solution: In triangle ABC, we are given the measures of two angles: ∠A = 37° and ∠C = 47°.
The sum of the interior angles of a triangle is always 180°. Therefore, we can use this information to find the measure of the unknown angle, ∠B.
∠A + ∠B + ∠C = 180° 37° + ∠B + 47° = 180° ∠B + 84° = 180° ∠B = 180° – 84° ∠B = 96°
Thus, the value of x is 96°, which is an obtuse angle.
Example 2: If the reflex angle measures 244°, what is the measure of the corresponding interior angle?
Solution: Given that the measure of the reflex angle is 244°.
To find the measure of the corresponding interior angle, we can use the relationship between reflex angles and interior angles.
Reflex angle + Interior angle = 360°
Let the measure of the interior angle be x.
Substituting the values into the equation: 244° + x = 360° x = 360° – 244° x = 116°
Therefore, the measure of the corresponding interior angle is 116°, which is an obtuse angle.
How Kunduz Can Help You Learn Obtuse Angles?
At Kunduz, we understand the importance of mastering geometric concepts like obtuse angles. That’s why we have developed a comprehensive and easy-to-follow online learning platform that caters to students of all ages and skill levels.
With Kunduz, you can access a wide range of interactive lessons, practice exercises, and quizzes that will help you understand obtuse angles and other mathematical concepts. Our platform is designed to make learning engaging and enjoyable, with personalized feedback and progress tracking to ensure your success.
Whether you’re a student looking to improve your math skills or a teacher seeking additional resources for your classroom, Kunduz is here to support you every step of the way. Join our community today and unlock the power of learning obtuse angles and beyond.