Öklid Teoremi Nedir?
Öklid teoremini dik bir üçgende hipotenüse ait yüksekliğin çizilmesi ve bu uzunluklar arasındaki bağıntı olarak değerlendirebiliriz.
Kısa öklid teoremini uygulayabilmek için;
- Dik üçgen
- Bu üçgende hipotenüse ait yükseklik çizilmiş olmalıdır.
Şekilde verilen ABC dik üçgeninde hipotenüse ait çizilmiş bir yükseklik olduğu için öklid kuralları uygulanabilir.
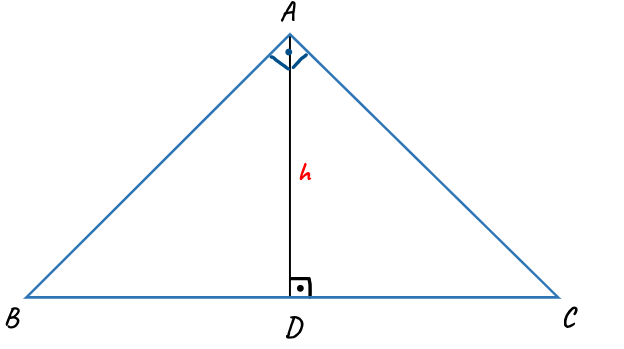
Öklid Formülü
Öklid bağıntı formüllerini şu şekilde sıralayabiliriz:
- h² = p.k
- c² = p.(p+k)
- b² = k.(p+k)
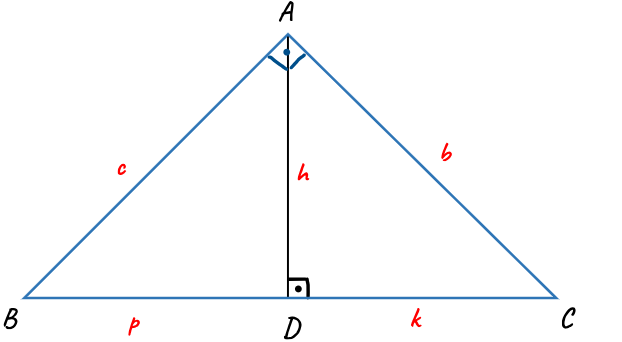
Öklid’in Yükseklik Bağıntısı
Öklid’in Yükseklik Bağıntısı, bir üçgenin içinde yer aldığı bir kenarı ve bu kenara ait yüksekliği arasındaki ilişkiyi ifade eder. Bu bağıntı, üçgenin benzer iki alt üçgeni arasındaki orantıdan türetilir.
Öklid’in Yükseklik Bağıntısı şu şekildedir:
Bir üçgenin bir kenarı üzerinde çizilmiş yüksekliğin, bu kenarı ait olan üçgenin hipotenüsüne bölünmüş uzunluğu, o üçgenin diğer iki kenarının uzunluklarından birine eşittir.
Bu bağıntıyı matematiksel ifade ile yazacak olursak:
h² = p.k
Burada:,
- h, üçgenin bir kenarı üzerine çizilmiş yüksekliğin uzunluğunu,
- p, hipotenüsü,
- k, hipotenüs üzerindeki kenara ait olan diğer kenarın uzunluğunu temsil eder.
Bu bağıntı, bir dik üçgenin kenar uzunlukları arasındaki ilişkiyi gösterir. Yükseklik, dik üçgenin hipotenüsüne dik olarak çizildiğinde, oluşan iki alt üçgenin benzer olduğu durumu ifade eder.
Üçgenlerde Benzerlik Kurallarından Yararlanarak Öklid Teoreminin İspatı
Öklid Teoremi, dik üçgenlerin hipotenüsü ve kenar uzunlukları arasındaki ilişkiyi ifade eder. Bu teorem, üçgen benzerlik kurallarını kullanarak kanıtlanabilir. İşte Öklid Teoremi’nin bir kanıtı:
Öklid Teoremi: Bir dik üçgenin hipotenüsünün karesi, diğer iki kenarın karelerinin toplamına eşittir.
Kanıt:
- ABC dik üçgenini düşünelim, burada AB hipotenüs, AC ve BC ise dik kenarlardır.
- Şimdi, ABC üçgeni içinde AC kenarı üzerine AD doğrusunu çizelim ve AD, BC kenarını C noktasında dik olarak kestiğini kabul edelim.
- Şimdi, △ABD ve △ADC üçgenleri arasında benzerlik olduğunu görelim. Bu benzerlik, iç açıların eşit olmasından kaynaklanır (bir açı 90 derecedir, diğer açılar her iki üçgende de eşittir).
- Benzer üçgenlerde kenar oranlarına göre ilişki kurabiliriz. AB/BD=AD/AC şeklinde bir benzerlik bağıntısı elde ederiz.
- Aynı şekilde, △ABC üçgeninde de benzerlik kurabiliriz ve AB/AC=AC/BC bağıntısını elde ederiz.
- Bu bağıntıyı düzenleyerek AB²=AC×BC elde ederiz.
- İki elde ettiğimiz ifadeyi birleştirerek, AB²=AD×BD=AC×BC elde ederiz.
- AB²=AC×BC ifadesi, Öklid Teoremi’ni kanıtlar.
Geometride Öklid Teoremi
- Bir şeye eşit olan iki şey, birbirine eşittir. (Öklid bağıntısının geçiş özelliği).
- Eşit olan ögelere, eşit miktarlar eklenirse bu ögeler yine eşit olur. (Eşitliğin toplama özelliği).
- Eşit olan ögelerden, eşit miktarlar çıkarılırsa bu ögeler yine eşit olur. (Eşitliğin çıkarma özelliği).
- Birbirleriyle çakışan şeyler, birbirine eşittir. (Yansıma özelliği)
- Bütün, parçadan daha büyüktür.
Öklid vs. Pisagor Farkları
| Özellik | Pisagor Teoremi | Öklid Teoremi |
|---|---|---|
| Keşif | Pisagor ve öğrencileri tarafından keşfedildi | Antik Yunan matematikçisi Öklid tarafından keşfedildi |
| Temel Formül | c² = a² + b² (dik üçgenler için) | h² = p.k |
| Genel Geometrik İlişkiler | Sadece dik üçgenlere özgüdür | Genel üçgen benzerlikleri ve diğer geometrik ilişkileri içerir |
Öklid Teoremi Günümüzde Ne İşe Yarar?
Öklid Teoremi, günümüzde hem matematikte hem de uygulamalı alanlarda önemli bir rol oynar. İşte Öklid Teoremi’nin günümüzdeki bazı önemli kullanım alanları:
- Geometri ve Matematik:
- Öklid Teoremi, matematikte temel bir konsepttir ve geometriyle ilgili birçok teorem ve kanıtın temelini oluşturur.
- Öklid geometrisi, Öklid Teoremi’nin temelinde yükselerek, düzlem geometrisinin birçok prensibini içerir.
- Mühendislik ve Fizik:
- Fizikte, özellikle de mekanik ve elektromanyetik alanlarda, vektörlerin ve kuvvetlerin analizinde Öklid Teoremi’nin prensipleri sıkça kullanılır.
- Yapı mühendisliği ve diğer mühendislik alanlarında, mesela bina planlamasında ve haritalarda, dik üçgenler ve Öklid Teoremi temel hesaplamalarda kullanılır.
- Bilgisayar Bilimi ve Görüntü İşleme:
- Bilgisayar biliminde, özellikle de grafikler ve görüntü işleme alanlarında, Öklid Teoremi’nin prensipleri çeşitli algoritmaların ve hesaplamaların temelini oluşturabilir.
- Optik ve Astronomi:
- Optik alanında, ayna ve lenslerin özellikleri Öklid Teoremi’ni içeren geometrik prensiplerle açıklanabilir.
- Astronomide, uzaklıkları ölçmek ve gök cisimlerinin konumlarını belirlemek için trigonometrik hesaplamalarda Öklid Teoremi’nin ilgili olduğu durumlar ortaya çıkabilir.
- Finans ve Ekonomi:
- Finans ve ekonomi alanında, özellikle risk ve getiri hesaplamalarında, Öklid Teoremi’nin trigonometrik fonksiyonları kullanılarak yapılan matematiksel hesaplamalara katkısı olabilir.
Öklid Teoremi’nin günümüzdeki çeşitli uygulama alanları, temel matematik prensiplerinin ve geometrik ilişkilerin geniş bir yelpazesini kapsar. Bu nedenle, Öklid Teoremi matematiksel düşünce ve uygulamalarda önemli bir rol oynamaya devam etmektedir.

