In the realm of mathematics, functions play a crucial role in mapping elements from one set to another. One important type of function is the one to one function, also known as an injective function. A one to one function is characterized by the fact that every element in the range is uniquely mapped to an element in the domain. In other words, the outputs of a one to one function never repeat.
Understanding the concept of one to one functions is essential in various branches of mathematics, including algebra, calculus, and linear algebra. In this article, we will explore the definition, properties, and examples of one to one functions to develop a comprehensive understanding of this important concept.
What is a One to One Function?
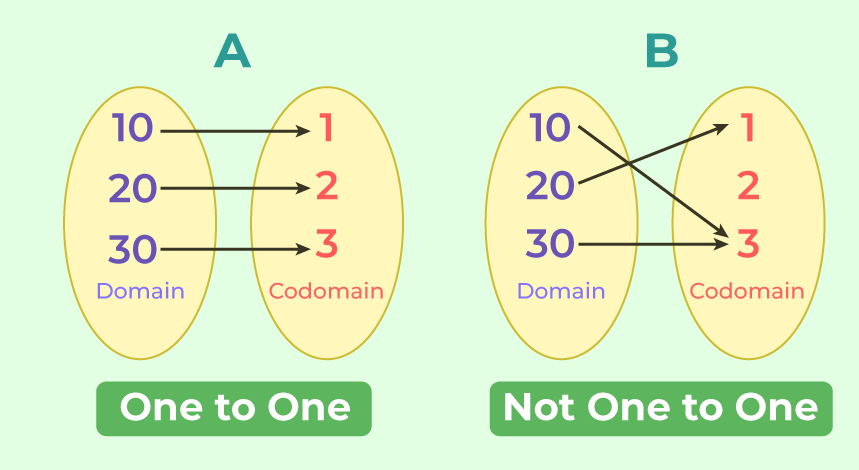
A one to one function is a type of function where each element in the domain is mapped to a unique element in the range. This ensures that no two different elements in the domain are mapped to the same element in the range. In simpler terms, a one to one function establishes a one-to-one correspondence between elements of the domain and elements of the range.
To mathematically define a one to one function, let’s consider a function f: A → B. This function is said to be one to one if and only if for any two distinct elements a and b in the domain A, f(a) is not equal to f(b). In other words, if f(a) = f(b), then a must be equal to b.
The one to one function is also known as an injective function because it injects each element of the domain into a unique element of the range. This property distinguishes it from other types of functions such as many to one functions, where multiple elements in the domain can map to the same element in the range.
One to One Graph: Horizontal Line Test
One way to determine whether a function is one to one is by using the horizontal line test. This test is performed by drawing horizontal lines on the graph of the function and observing how many times each line intersects the graph.
If a horizontal line intersects the graph of a function at more than one point, then the function is not one to one. This indicates that multiple elements in the domain are mapped to the same element in the range. On the other hand, if a horizontal line intersects the graph at most once, then the function is one to one.
Consider the graph of the function f(x) = x². If we draw a horizontal line, we can see that it intersects the graph at multiple points, indicating that the function is not one to one. In contrast, the graph of the function f(x) = x is a straight line that passes the horizontal line test, making it a one to one function.
The horizontal line test provides a visual representation of the one to one property of a function and can help determine whether a given function is one to one or not.
One to One Function Inverse
The concept of inverse functions is closely related to one to one functions. An inverse function undoes the action of the original function, allowing us to retrieve the initial input value from the output value. In other words, if we have a one to one function f(x), its inverse function, denoted as f^(-1)(x), will reverse the mapping, allowing us to find the original input value.
The inverse of a one to one function is defined as follows: If f is a function from a set A to a set B, then the inverse of f, denoted as f^(-1), is a function from B to A such that f^(-1)(f(a)) = a for every element a in A and f(f^(-1)(b)) = b for every element b in B.
To find the inverse of a one to one function, we can follow a step-by-step process:
- Write the function in the form y = f(x).
- Interchange x and y in the equation.
- Solve the equation for y.
- Rename y as f^(-1)(x).
For example, let’s find the inverse of the function f(x) = 2x + 3:
- Write the function in the form y = f(x): y = 2x + 3.
- Interchange x and y: x = 2y + 3.
- Solve for y: y = (x – 3)/2.
- Rename y as f^(-1)(x): f^(-1)(x) = (x – 3)/2.
The inverse function allows us to recover the original input value from the output value, making it a powerful tool in mathematical analysis and problem-solving.
Steps to Find the Inverse of One to One Function
Finding the inverse of a one to one function involves following a systematic series of steps. By following these steps, we can determine the inverse function and establish a one-to-one correspondence between the elements of the domain and the range. Here are the steps to find the inverse of a one to one function:
- Start with the original function, f(x), which is known to be one to one.
- Replace f(x) with y to represent the function in terms of y.
- Interchange x and y, resulting in an equation of the form x = f^(-1)(y).
- Solve the equation for y to express the inverse function, f^(-1)(y), in terms of y.
- Rename y as x to represent the inverse function as f^(-1)(x).
Following these steps allows us to find the inverse of a one to one function, establishing a relationship between the original function and its inverse.
How to Determine if a Function is One to One?
Determining whether a given function is one to one involves analyzing its properties and characteristics. While there are multiple approaches to determine if a function is one to one, two common methods are algebraic analysis and graphical analysis.
Algebraic analysis involves examining the equation of the function and applying mathematical techniques to determine if it satisfies the criteria for a one to one function. This often involves comparing the outputs of the function for different inputs and checking if they are unique.
For example, let’s consider the function f(x) = x². To determine if this function is one to one, we can compare the outputs for different inputs. If we find two inputs, say a and b, such that f(a) = f(b), but a ≠ b, then the function is not one to one. In the case of f(x) = x², we can see that f(2) = f(-2), but 2 ≠ -2. Therefore, the function is not one to one.
Graphical analysis involves plotting the function on a coordinate plane and examining its graph for any patterns or characteristics that indicate a one to one relationship. One common graphical test is the horizontal line test. If a horizontal line intersects the graph of the function at more than one point, then the function is not one to one. On the other hand, if the horizontal line intersects the graph at most once, then the function is one to one.
For example, let’s consider the function g(x) = 2x + 3. By graphing this function and observing that a horizontal line intersects the graph at most once, we can conclude that the function is one to one.
By applying these algebraic and graphical analysis techniques, we can determine whether a given function is one to one or not.
Properties of One to One Function
One to one functions possess certain properties that distinguish them from other types of functions. Understanding these properties can help us identify and analyze one to one functions. Here are some key properties of one to one functions:
- Composition: If two functions, f and g, are both one to one, then the composition function f o g (read as f composed with g) is also a one to one function. This property allows us to combine multiple one to one functions to create new one to one functions.
- Inverse: Every one to one function has an inverse function. The inverse function undoes the action of the original function, allowing us to retrieve the original input value from the output value. The domain of the inverse function is the range of the original function, and the range of the inverse function is the domain of the original function.
- Domain and Range: The domain of a one to one function is equal to the range of its inverse function, and the range of the one to one function is equal to the domain of its inverse function. This property establishes a one to one correspondence between the elements of the domain and range.
- Intersection of Sets: If a one to one function f maps a subset P of the domain to a subset Q of the range, then the intersection of f(P) and f(Q) is equal to f(P ∩ Q). This property demonstrates how the one to one function preserves the intersection of sets.
- Cardinality: If both the domain and range of a one to one function have the same number of elements, then the function is one to one. This property highlights the equal mapping between elements of the domain and range.
Understanding these properties allows us to analyze and manipulate one to one functions, enabling us to solve mathematical problems and explore various applications.
One to One Function and Onto Function
One to one functions and onto functions are two important concepts in mathematical analysis. While one to one functions establish a unique mapping between the elements of the domain and range, onto functions ensure that every element in the codomain is mapped to by at least one element in the domain.
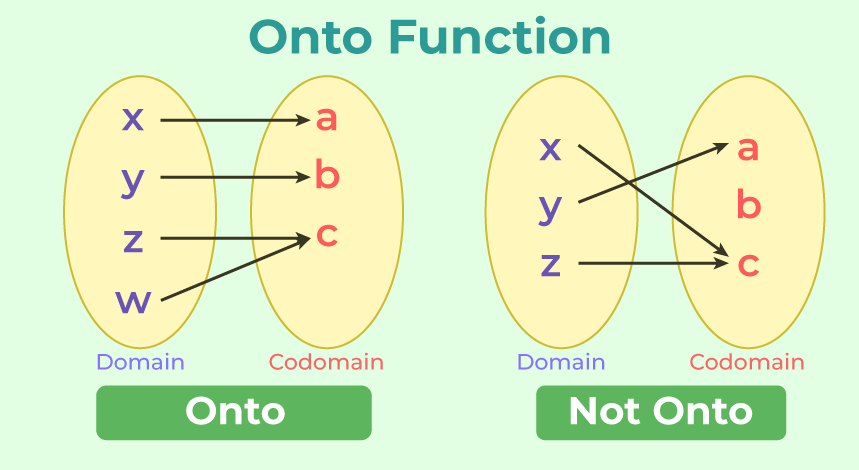
An onto function, also known as a surjective function, is a function where every element in the codomain is mapped to by at least one element in the domain. In other words, the range of the function equals the entire codomain. This ensures that there are no “gaps” in the mapping, and every element in the codomain has a corresponding element in the domain.
In contrast, a one to one function does not allow multiple elements in the domain to map to the same element in the range. It establishes a one-to-one correspondence between the elements of the domain and range, ensuring that each element in the domain is uniquely mapped to an element in the range.
It is important to note that a function can be both one to one and onto, in which case it is called a bijective function. Bijective functions establish a one-to-one correspondence between the elements of the domain and range, with no repetitions or gaps in the mapping.
Understanding the distinction between one to one functions and onto functions allows us to analyze and classify different types of functions based on their mapping properties.
What Types of Functions are One-to-One?
One to one functions can take various forms and can be found in different branches of mathematics. Here are some common types of functions that are one to one:
- Linear Functions: A linear function of the form f(x) = mx + b, where m and b are constants, is always one to one. Each input value x corresponds to a unique output value f(x), ensuring that no two different inputs map to the same output.
- Identity Function: The identity function is a simple example of a one to one function. It takes an input and returns the same value as the output. For any set of elements, the identity function maps each element to itself, creating a one-to-one correspondence.
- Exponential Functions: Exponential functions of the form f(x) = a^x, where a is a positive constant, are one to one functions. The exponential growth or decay ensures that each input value x maps to a unique output value f(x), making it a one to one function.
- Trigonometric Functions: Trigonometric functions such as sine, cosine, and tangent are one to one functions over specific intervals. For example, the sine function is one to one over the interval [-π/2, π/2], ensuring that each input value corresponds to a unique output value.
These are just a few examples of the types of functions that can be one to one. In general, any function that establishes a unique mapping between the elements of the domain and range without repetitions or gaps is considered a one to one function.
Strictly Increasing and Strictly Decreasing Function
Strictly increasing and strictly decreasing functions are specific types of one to one functions that exhibit certain ordering properties. These functions have a consistent trend in their mapping, either increasing or decreasing, without any reversals or repetitions.
A strictly increasing function is a one to one function where the outputs are always greater than the inputs. In other words, if a < b, then f(a) < f(b) for all elements a and b in the domain. The graph of a strictly increasing function rises from left to right with no reversals or plateaus.
Conversely, a strictly decreasing function is a one to one function where the outputs are always less than the inputs. In other words, if a < b, then f(a) > f(b) for all elements a and b in the domain. The graph of a strictly decreasing function descends from left to right with no reversals or plateaus.
Strictly increasing and strictly decreasing functions are important in various mathematical applications, such as optimization problems and calculus. Their one to one property ensures that each input value corresponds to a unique output value, allowing for precise analysis and modeling.
What is Onto Function?
An onto function, also known as a surjective function, is a type of function where every element in the codomain is mapped to by at least one element in the domain. In other words, the function covers the entire range of the codomain without leaving any “gaps”.
Formally, a function f: A → B is considered onto if and only if for every element y in the codomain B, there exists at least one element x in the domain A such that f(x) = y. This ensures that every element in the codomain has a corresponding element in the domain.
Onto functions are characterized by their ability to cover the entire range of the codomain. Unlike one to one functions, where each element in the domain maps to a unique element in the range, onto functions allow for multiple elements in the domain to map to the same element in the codomain.
For example, consider the function f(x) = x². While this function is not one to one since different inputs can produce the same output, it is onto because every non-negative real number has a corresponding input value whose square is equal to that number.
Onto functions are frequently used in various mathematical applications, such as function composition, set theory, and mathematical modeling. They play a crucial role in establishing mappings and relationships between different sets of elements.
Proving that Functions are Injective
Proving that a function is one to one, or injective, involves demonstrating that no two distinct elements in the domain map to the same element in the range. There are multiple methods to prove that a function is injective, depending on the properties and characteristics of the function. Here are some common methods:
- Algebraic Proof: One way to prove that a given function is injective is by using an algebraic proof. This involves assuming that two distinct elements in the domain map to the same element in the range and then reaching a contradiction. By assuming that f(a) = f(b) for a ≠ b, we can manipulate the equation and show that it leads to a contradiction. This contradiction proves that the function is injective.
- Using the Definition: Another method to prove injectivity is by using the definition of a one to one function. Recall that a function f is injective if and only if f(a) = f(b) implies a = b for all elements a and b in the domain. By applying this definition and demonstrating that the implication holds true for the given function, we can prove that it is injective.
- Graphical Proof: In some cases, the graph of a function can provide evidence for its injectivity. If a horizontal line intersects the graph at most once, then the function is injective. By visually inspecting the graph and observing that the horizontal line test is satisfied, we can conclude that the function is injective.
These are just a few methods to prove that a function is injective. The specific approach will depend on the properties and characteristics of the function being analyzed. By applying rigorous mathematical reasoning and evidence, we can establish the injectivity of a given function.
Solved Examples on One to One Function
Let’s solve some examples to illustrate the concept of one to one functions and demonstrate how to determine whether a given function is one to one.
Example 1: Determine whether the following function is one to one: f(x) = 3x – 1.
Solution: To check if the function is one to one, we need to show that no two distinct x-values map to the same y-value.
Suppose f(a) = f(b), where a ≠ b. 3a – 1 = 3b – 1 3a = 3b a = b
Since the only way for f(a) = f(b) is when a = b, this function is indeed one to one.
Example 2: Determine whether the following function is one to one: g(x) = x².
Solution: We can use the horizontal line test to determine if the function is one to one. By examining the graph of the function, we can see that a horizontal line intersects the graph at multiple points. Therefore, the function is not one to one.
Example 3: Find the inverse function of f(x) = 4x – 7 and determine its domain.
Solution: To find the inverse function, we can follow the steps outlined earlier:
- Write the function in the form y = f(x): y = 4x – 7.
- Interchange x and y: x = 4y – 7.
- Solve for y: y = (x + 7)/4.
- Rename y as f^(-1)(x): f^(-1)(x) = (x + 7)/4.
The domain of the inverse function is the same as the range of the original function, which is all real numbers.
By solving these examples, we can practice analyzing functions and determining whether they are one to one or not. These examples demonstrate the importance of careful examination and understanding of the properties of one to one functions.
How Kunduz Can Help You Learn One to One Function?
At Kunduz, we understand the importance of a strong foundation in mathematics. That’s why we offer comprehensive learning resources to help students excel in their math studies. Our expert instructors provide step-by-step explanations, practice problems, and real-life applications to ensure a deep understanding of one to one functions.
Whether you’re preparing for a math exam, seeking additional support in your coursework, or simply looking to enhance your mathematical skills, Kunduz can help. Our user-friendly platform offers a wide range of educational materials, including video lessons, interactive quizzes, and personalized tutoring sessions.
With Kunduz, you can learn at your own pace, access high-quality resources, and receive expert guidance from experienced instructors. We are dedicated to helping students succeed in their math studies and develop a solid foundation in mathematical concepts.
So, whether you’re struggling with one to one functions or looking to expand your mathematical knowledge, Kunduz is here to assist you every step of the way. Join us today and unlock your full math potential.
