In the world of statistics, the p-value holds significant importance. It is a crucial measure that helps researchers determine the strength of the evidence against the null hypothesis. By calculating the p-value, one can assess the likelihood of observing a particular set of data or more extreme results if the null hypothesis were true. This powerful statistical tool is widely used in hypothesis testing to make informed decisions about accepting or rejecting the null hypothesis.
What is P-Value?
The p-value, short for probability value, is a numerical representation of the likelihood of obtaining results as extreme or more extreme than the observed data under the assumption that the null hypothesis is true. It quantifies the evidence against the null hypothesis and provides insights into the statistical significance of the results. A small p-value suggests stronger evidence against the null hypothesis and indicates that the observed data is unlikely to occur by chance alone.
P-Value Formula
The calculation of the p-value depends on the specific statistical test being used. However, there is a common formula that is widely used to calculate the p-value in various tests. The formula is as follows:
p-value = P(test statistic ≥ observed value | null hypothesis is true)
The test statistic is calculated based on the data and the null hypothesis. By comparing the test statistic to the observed value, the p-value is determined. The p-value represents the probability of obtaining results as extreme or more extreme than the observed data if the null hypothesis were true.
How to Find P-Value Formula?
Finding the p-value involves several steps. Let’s break down the process step by step:
Step 1: Formulate the Null and Alternative Hypotheses
Before calculating the p-value, it is essential to define the null hypothesis (H0) and the alternative hypothesis (HA). The null hypothesis assumes no difference or no relationship between variables, while the alternative hypothesis predicts a difference or a relationship.
Step 2: Select the Appropriate Statistical Test
Choose the appropriate statistical test based on the research question and the type of data being analyzed. Different tests, such as t-tests, z-tests, and chi-square tests, require specific formulas to calculate the p-value.
Step 3: Calculate the Test Statistic
Calculate the test statistic based on the chosen statistical test and the data. The test statistic measures the distance between the observed data and the expected values under the null hypothesis.
Step 4: Determine the p-value
Compare the test statistic to the distribution of test statistics under the null hypothesis. This comparison allows you to determine the probability of obtaining a test statistic as extreme or more extreme than the observed value. The resulting probability is the p-value.
Exploring the P-Value Properties
The p-value possesses several properties that are important to understand its significance:
1. The p-value ranges from 0 to 1: The p-value is always between 0 and 1, representing the probability of observing the data or more extreme results under the null hypothesis.
2. A small p-value indicates strong evidence against the null hypothesis: A p-value less than a predetermined significance level (such as 0.05 or 0.01) suggests that the observed data is unlikely to occur by chance alone. It provides strong evidence against the null hypothesis.
3. The significance level determines the threshold for rejecting the null hypothesis: The significance level, often denoted as alpha (α), is a predetermined threshold that determines the level of evidence required to reject the null hypothesis. The p-value is compared to the significance level to make a decision about the null hypothesis.
4. The p-value does not measure the strength of the effect: The p-value only quantifies the evidence against the null hypothesis. It does not provide information about the magnitude or importance of the observed effect.
P-Value Table
To interpret the p-value, researchers often refer to a p-value table. This table provides guidelines for interpreting the p-value based on different significance levels. Here is an example of a p-value table:
| P-value | Description | Hypothesis Interpretation |
|---|---|---|
| ≤ 0.05 | Statistically significant | Reject the null hypothesis |
| > 0.05 | Not statistically significant | Fail to reject the null hypothesis |
By comparing the calculated p-value to the significance level (usually 0.05), researchers can determine whether the results are statistically significant or not.
How to find P value from t-test?
The t-test is a statistical test used to compare the means of two groups. To find the p-value from a t-test, follow these steps:
Step 1: Formulate the Null and Alternative Hypotheses
Define the null hypothesis (H0) and the alternative hypothesis (HA) based on the research question. The null hypothesis usually assumes no difference between the means of the two groups.
Step 2: Calculate the Test Statistic
Compute the test statistic for the t-test using the formula:
t = (x̄1 – x̄2) / √((s1^2 / n1) + (s2^2 / n2))
where x̄1 and x̄2 are the sample means, s1 and s2 are the sample standard deviations, and n1 and n2 are the sample sizes.
Step 3: Determine the Degrees of Freedom
The degrees of freedom for the t-test are calculated using the formula:
df = n1 + n2 – 2
where n1 and n2 are the sample sizes of the two groups.
Step 4: Find the p-value
Look up the test statistic and degrees of freedom in a t-distribution table or use statistical software to determine the corresponding p-value. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed value under the null hypothesis.
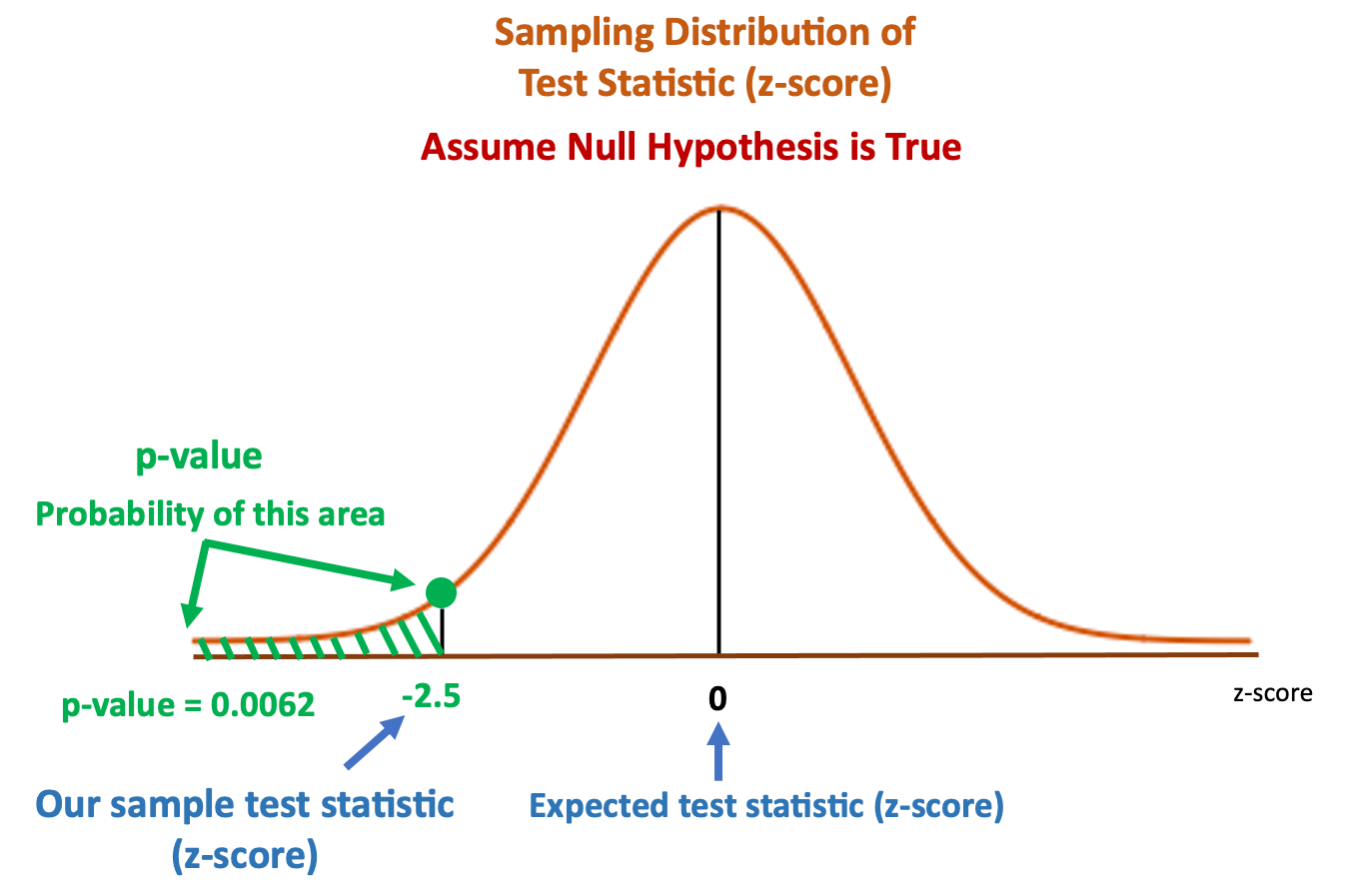
How to find P value from z-score?
The z-test is used when the population standard deviation is known. To find the p-value from a z-test, follow these steps:
Step 1: Formulate the Null and Alternative Hypotheses
Define the null hypothesis (H0) and the alternative hypothesis (HA) based on the research question.
Step 2: Calculate the Test Statistic
Compute the test statistic for the z-test using the formula:
z = (x̄ – μ) / (σ / √n)
where x̄ is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
Step 3: Find the p-value
Look up the test statistic in a standard normal distribution table or use statistical software to determine the corresponding p-value. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed value under the null hypothesis.
How to find the p-value from the chi-square test?
The chi-square test is used to determine if there is an association between two categorical variables. To find the p-value from a chi-square test, follow these steps:
Step 1: Formulate the Null and Alternative Hypotheses
Define the null hypothesis (H0) and the alternative hypothesis (HA) based on the research question.
Step 2: Calculate the Test Statistic
Compute the test statistic for the chi-square test using the formula:
χ^2 = ∑((O – E)^2 / E)
where O is the observed frequency and E is the expected frequency.
Step 3: Determine the Degrees of Freedom
The degrees of freedom for the chi-square test are calculated using the formula:
df = (r – 1) x (c – 1)
where r is the number of rows and c is the number of columns in the contingency table.
Step 4: Find the p-value
Look up the test statistic and degrees of freedom in a chi-square distribution table or use statistical software to determine the corresponding p-value. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed value under the null hypothesis.
Solved Examples on P-Value
Let’s explore a few examples to better understand how to calculate and interpret the p-value:
Example 1: A researcher wants to test if there is a significant difference in test scores between two groups of students. A t-test is conducted, and the calculated t-value is -2.16. Given a significance level of 0.05, determine the p-value and interpret the results.
Solution: Using a t-distribution table or statistical software, the p-value corresponding to a t-value of -2.16 with the appropriate degrees of freedom is found to be approximately 0.034. Since the p-value is less than the significance level of 0.05, we can conclude that there is a statistically significant difference in test scores between the two groups.
Example 2: In a study comparing the effectiveness of two different medications, a chi-square test is conducted, and the calculated chi-square statistic is 14.36. With 3 degrees of freedom, find the p-value and interpret the results.
Solution: Using a chi-square distribution table or statistical software, the p-value corresponding to a chi-square statistic of 14.36 with 3 degrees of freedom is found to be less than 0.001. Since the p-value is significantly less than the significance level of 0.05, we can conclude that there is a statistically significant association between the type of medication and its effectiveness.
How Kunduz Can Help You Learn P-Value?
With Kunduz, you can gain the confidence and skills necessary to excel in your statistical analyses and research endeavors.
Unlock the power of the p-value with Kunduz and take your statistical knowledge to new heights. Start exploring our resources today and embark on a journey of statistical mastery.
