A parallelogram is a two-dimensional geometric shape with special properties that make it unique. In this article, we will explore the definition of a parallelogram, its properties, various formulas related to its area and perimeter, and provide examples to help solidify your understanding.
An Introduction to Parallelogram
A parallelogram is a quadrilateral, which means it has four sides. What sets a parallelogram apart from other quadrilaterals is that its opposite sides are parallel and equal in length. This means that if you were to extend the sides of a parallelogram, they would never intersect. Additionally, a parallelogram has two pairs of opposite angles that are equal in measure.
What is a Parallelogram?
A parallelogram can be defined as a quadrilateral with two pairs of opposite sides that are parallel and equal in length. This unique property gives the parallelogram its distinctive shape. In a parallelogram, the opposite angles are also equal. This means that if you were to measure the angles formed by the intersecting sides of a parallelogram, you would find that the opposite angles are congruent.

Parallelogram Formulas
There are several important formulas related to parallelograms that can help us calculate various measurements. Let’s take a look at two of the most common formulas used to find the area and perimeter of a parallelogram.
Area of a Parallelogram
The area of a parallelogram can be calculated by multiplying the base (the length of one of the parallel sides) by the height (the perpendicular distance between the base and the opposite side). The formula for the area of a parallelogram is:
Area = Base × Height
Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around its boundary, which is the sum of all its sides. Since a parallelogram has two pairs of parallel sides, its perimeter can also be expressed as twice the sum of the lengths of its adjacent sides. The formula for the perimeter of a parallelogram is:
Perimeter = 2 × (Side1 + Side2)
Angles of Parallelogram
The angles of a parallelogram have some interesting properties. The most important property is that the opposite angles of a parallelogram are equal. This means that if we label the angles of a parallelogram as A, B, C, and D, then ∠A = ∠C and ∠B = ∠D.
Another property of parallelogram angles is that the consecutive angles (angles that share a side) are supplementary, meaning that their sum is equal to 180 degrees. In other words, ∠A + ∠B = 180 degrees and ∠C + ∠D = 180 degrees.
Properties of Parallelogram
Parallelograms have several properties that distinguish them from other quadrilaterals. Understanding these properties can help us identify and work with parallelograms more effectively. Let’s explore some of the key properties of parallelograms:
- Opposite sides: The opposite sides of a parallelogram are parallel and equal in length. This means that if we were to extend the sides of a parallelogram, they would never intersect.
- Opposite angles: The opposite angles of a parallelogram are equal in measure. This means that if we were to measure the angles formed by the intersecting sides of a parallelogram, we would find that the opposite angles are congruent.
- Diagonals: The diagonals of a parallelogram bisect each other. In other words, they divide each other into two equal parts. This property can be observed by drawing the diagonals of a parallelogram and noticing that they intersect at their midpoints.
- Consecutive angles: The consecutive angles of a parallelogram are supplementary. This means that the sum of any two consecutive angles is equal to 180 degrees. For example, ∠A + ∠B = 180 degrees and ∠B + ∠C = 180 degrees.
Parallelogram Structure
A parallelogram has a distinct structure that sets it apart from other shapes. It is a quadrilateral, which means it has four sides. The opposite sides of a parallelogram are parallel and equal in length. Additionally, the opposite angles of a parallelogram are equal in measure. This unique structure gives the parallelogram its characteristic shape.
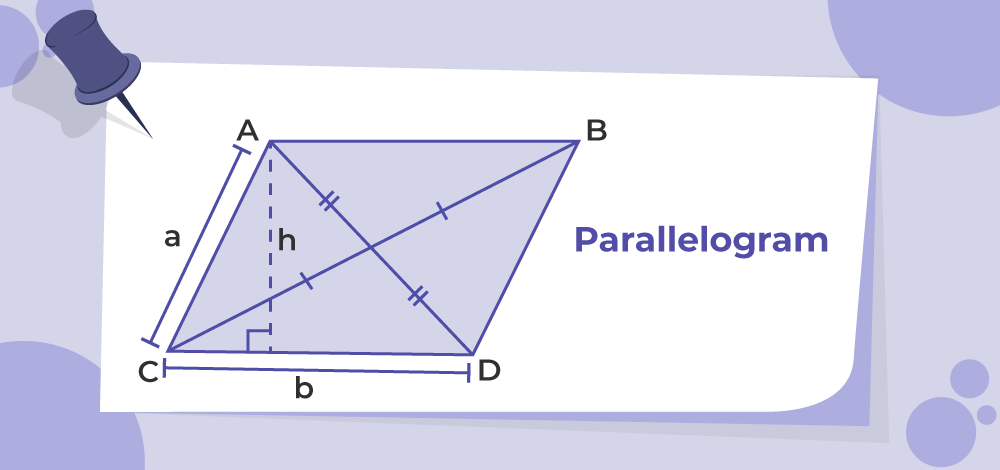
Parallelogram Shape Characteristics
The shape of a parallelogram can be described as a four-sided figure with opposite sides that are parallel and equal in length. This unique shape gives the parallelogram several defining characteristics:
- Base: Any side of a parallelogram can be considered as the base. The base is typically used to calculate the area of the parallelogram.
- Altitude (Height): The altitude, or height, of a parallelogram is the perpendicular distance between the base and the opposite side. It is used to calculate the area of the parallelogram.
- Area: The area of a parallelogram can be calculated by multiplying the base by the height. The formula for finding the area of a parallelogram is: Area = Base × Height.
- Perimeter: The perimeter of a parallelogram is the total length of its boundary. It can be calculated by adding the lengths of all four sides of the parallelogram.
Parallelogram of Octagon
A parallelogram is a special type of quadrilateral, and it serves as the parent shape for other quadrilaterals. One example of a parallelogram is the octagon, which is an eight-sided polygon. Let’s explore some of the different types of parallelograms that can be formed from an octagon.
Rectangle
A rectangle is a type of parallelogram with four right angles. This means that all four interior angles of a rectangle are equal to 90 degrees. Additionally, a rectangle has two pairs of opposite sides that are parallel and equal in length.
Square
A square is a special type of rectangle where all four sides are equal in length. In addition to having four right angles, a square also has two pairs of opposite sides that are parallel.
Rhombus
A rhombus is another type of parallelogram that has four sides of equal length. Like other parallelograms, a rhombus has opposite sides that are parallel. However, unlike a rectangle or square, the angles of a rhombus are not necessarily right angles.
Difference Between Parallelogram and Rectangle
While both parallelograms and rectangles are types of quadrilaterals, there are some key differences between them. Let’s explore the differences between a parallelogram and a rectangle.
Difference Between Parallelogram and Rectangle – Properties
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. It has opposite angles that are equal in measure. On the other hand, a rectangle is a type of parallelogram that has four right angles. This means that all four interior angles of a rectangle are equal to 90 degrees.
Difference Between Parallelogram and Rectangle – Sides
In a parallelogram, the opposite sides are equal in length and parallel. However, in a rectangle, all four sides are equal in length and parallel. This means that while a rectangle is a type of parallelogram, not all parallelograms are rectangles.
Difference Between Parallelogram and Rhombus
A parallelogram and a rhombus are both types of quadrilaterals, but they have some distinct differences. Let’s explore the differences between a parallelogram and a rhombus.
Difference Between Parallelogram and Rhombus – Sides
In a parallelogram, the opposite sides are equal in length and parallel. However, in a rhombus, all four sides are equal in length. This means that while a rhombus is a type of parallelogram, not all parallelograms are rhombuses.
Difference Between Parallelogram and Rhombus – Angles
While a parallelogram has opposite angles that are equal in measure, a rhombus does not necessarily have right angles. In a rhombus, the opposite angles are equal, but they can be any angle other than 90 degrees.
Difference Between Parallelogram and Quadrilateral
A parallelogram and a quadrilateral are both types of polygons, but they have some distinct differences. Let’s explore the differences between a parallelogram and a quadrilateral.
Difference Between Parallelogram and Quadrilateral – Definition
A parallelogram is a specific type of quadrilateral with opposite sides that are parallel and equal in length. This means that a parallelogram is a subset of quadrilaterals that have these specific properties.
Difference Between Parallelogram and Quadrilateral – Properties
While all parallelograms are quadrilaterals, not all quadrilaterals are parallelograms. A quadrilateral is a general term that refers to any four-sided polygon. It can have different combinations of side lengths and angle measures, whereas a parallelogram has specific properties that set it apart from other quadrilaterals.
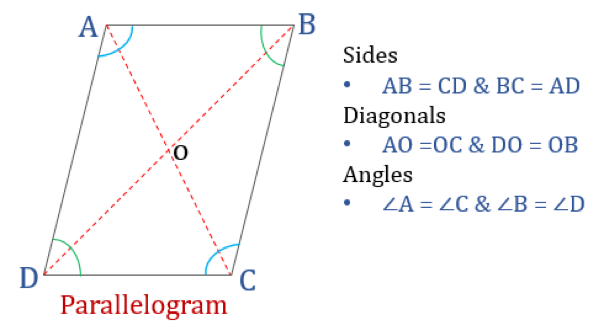
Parts of a Parallelogram
A parallelogram has several parts that contribute to its overall shape and structure. Let’s explore the different parts of a parallelogram:
- Base: The base of a parallelogram is one of its parallel sides. It can be any one of the four sides, and it is typically used to calculate the area of the parallelogram.
- Height (Altitude): The height, or altitude, of a parallelogram is the perpendicular distance between the base and the opposite side. It is used to calculate the area of the parallelogram.
- Diagonals: A parallelogram has two diagonals, which are line segments that connect opposite vertices. The diagonals of a parallelogram bisect each other, meaning they divide each other into two equal parts.
- Angles: A parallelogram has four angles, labeled ∠A, ∠B, ∠C, and ∠D. The opposite angles of a parallelogram are equal, and the consecutive angles are supplementary, meaning their sum is equal to 180 degrees.
Parallelogram Theorems
There are several theorems related to parallelograms that provide additional insights into their properties and relationships with other shapes. Let’s explore some of the key theorems related to parallelograms:
- Theorem 1: Parallelograms on the same base and between the same parallels are equal in area. This theorem states that if two parallelograms have the same base and are located between the same parallel lines, their areas are equal.
- Corollary: A parallelogram and a rectangle on the same base and between the same parallels are equal in area. This corollary builds upon the first theorem by stating that if a parallelogram and a rectangle have the same base and are located between the same parallel lines, their areas are equal.
- Theorem 2: The area of a parallelogram is the product of its base and the corresponding altitude. This theorem provides a formula for calculating the area of a parallelogram: Area = Base × Altitude.
Parallelogram inscribed in any quadrilateral
One interesting property of parallelograms is that they can be inscribed in any quadrilateral. This means that if you take any quadrilateral and connect the midpoints of its sides, the resulting figure will always be a parallelogram.
This property can be proven by examining the midpoints of each side of a quadrilateral and connecting them sequentially with lines. When these lines are drawn, they form a parallelogram.
This property is useful in geometry as it allows us to analyze and understand the relationships between different quadrilaterals. It also highlights the flexibility and versatility of parallelograms in various geometric configurations.
Frequently Asked Questions on Parallelogram
Let’s address some frequently asked questions about parallelograms to further enhance our understanding:
How Many Sides Does a Parallelogram Have?
A parallelogram has four sides, just like any other quadrilateral. The four sides of a parallelogram are connected by four vertices to form its shape.
Is a Rectangle a Parallelogram?
Yes, a rectangle is a specific type of parallelogram. A rectangle has all the properties of a parallelogram, such as having opposite sides that are parallel and equal in length. Additionally, a rectangle has the unique property of having all four interior angles equal to 90 degrees.
Is a Rhombus a Parallelogram?
Yes, a rhombus is also a type of parallelogram. A rhombus has all the properties of a parallelogram, such as having opposite sides that are parallel and equal in length. Additionally, a rhombus has the unique property of having all four sides equal in length.
Is a Parallelogram a Quadrilateral?
Yes, a parallelogram is a type of quadrilateral. A quadrilateral is a polygon with four sides, and a parallelogram fits this definition. However, not all quadrilaterals are parallelograms, as they may not have opposite sides that are parallel and equal in length.
How to Find the Area of a Parallelogram?
To find the area of a parallelogram, you need to know the length of its base and the corresponding altitude. The formula for finding the area of a parallelogram is: Area = Base × Height. By multiplying the base by the height, you can calculate the area of the parallelogram.
How to Find the Perimeter of a Parallelogram?
To find the perimeter of a parallelogram, you need to add the lengths of all four sides. Since a parallelogram has two pairs of equal and parallel sides, its perimeter can also be calculated as twice the sum of the lengths of its adjacent sides. By adding the lengths of the sides, you can find the perimeter of the parallelogram.
Is a Trapezoid a Parallelogram?
No, a trapezoid is not a parallelogram. A trapezoid is a quadrilateral with one pair of opposite sides that are parallel. In contrast, a parallelogram has two pairs of opposite sides that are parallel. While a parallelogram can be a trapezoid, not all trapezoids are parallelograms.
Do Angles in a Parallelogram Sum Up to 360°?
Yes, the sum of all four interior angles of a parallelogram is equal to 360 degrees. This is because a parallelogram is a quadrilateral, and the sum of the interior angles of any quadrilateral is always 360 degrees.
Are all Parallelogram Sides Congruent?
In a parallelogram, the opposite sides are congruent, meaning they are equal in length. However, the adjacent sides of a parallelogram may not be congruent. The congruence of sides depends on the specific properties of the parallelogram.
Solved Examples on Parallelogram
Let’s work through some examples to practice applying the concepts we’ve learned about parallelograms.
Example 1: Finding the Area of a Parallelogram
Given a parallelogram with a base of 10 cm and a height of 8 cm, find the area.
To find the area of a parallelogram, we can use the formula Area = Base × Height. Substituting the given values, we have:
Area = 10 cm × 8 cm = 80 cm²
Therefore, the area of the parallelogram is 80 cm².
Example 2: Finding the Perimeter of a Parallelogram
Given a parallelogram with side lengths of 5 cm and 8 cm, find the perimeter.
To find the perimeter of a parallelogram, we can use the formula Perimeter = 2 × (Side₁ + Side₂). Substituting the given values, we have:
Perimeter = 2 × (5 cm + 8 cm) = 2 × 13 cm = 26 cm
Therefore, the perimeter of the parallelogram is 26 cm.
How Kunduz Can Help You Learn Parallelograms?
At Kunduz, we understand the importance of mastering key mathematical concepts like parallelograms. That’s why we offer a wide range of resources, including interactive lessons, practice exercises, and helpful guides, to help you learn and understand parallelograms with ease. Our expert instructors are dedicated to providing clear and concise explanations, ensuring that you have a solid foundation in geometry.
Whether you’re a student looking to improve your math skills or a teacher seeking additional resources for your classroom, Kunduz is here to support you every step of the way. Join us today and unlock the power of learning.
