In the world of geometry, polygons are a fascinating subject of study. These two-dimensional shapes are composed of straight sides and interior angles. One such polygon is the pentagon, which is a five-sided shape. The word “pentagon” is derived from the Greek words “penta,” meaning “five,” and “gonia,” meaning “angle.” In this article, we will explore the definition, properties, types, and formulas related to the pentagon shape.
Pentagon Definition
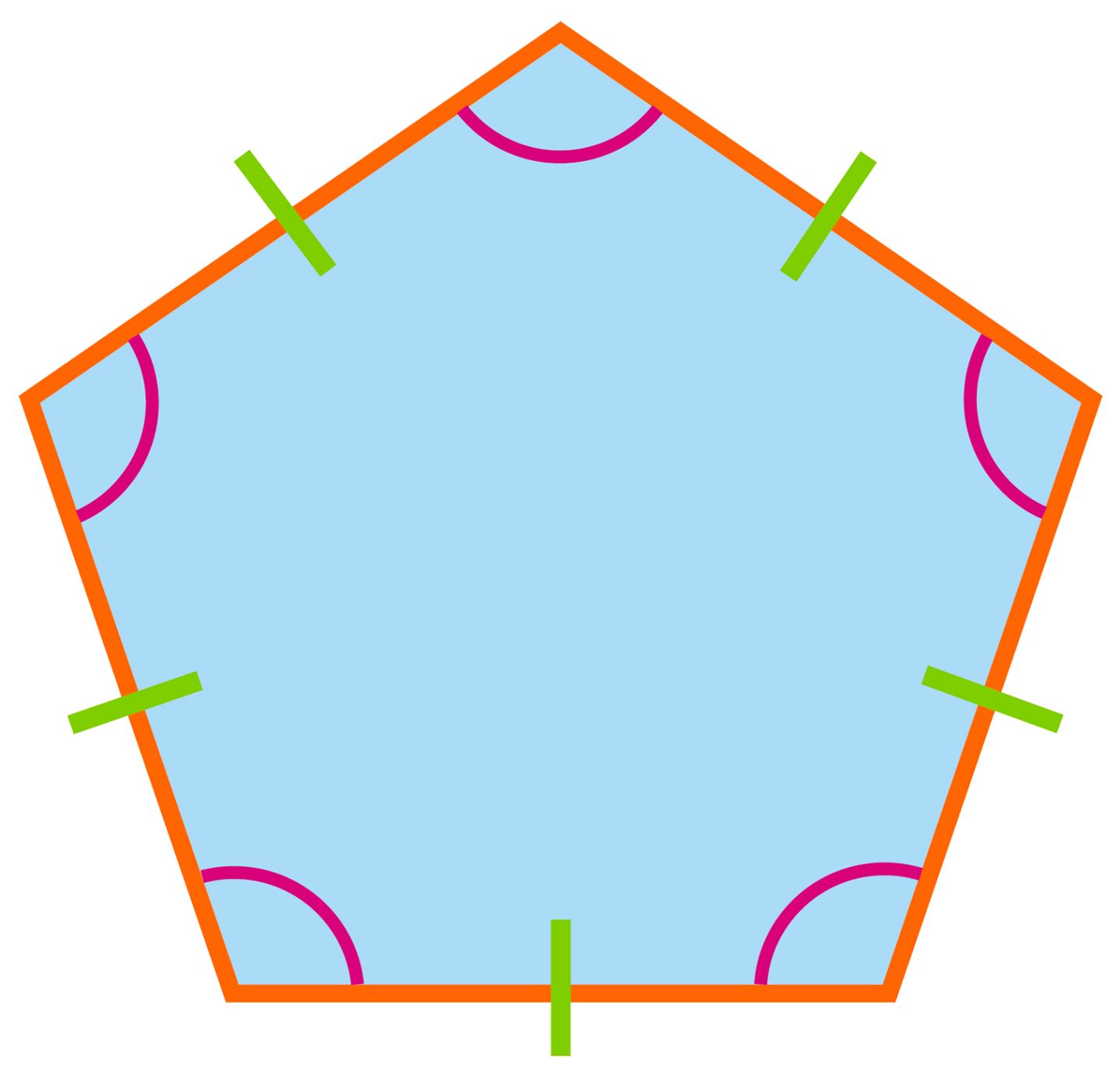
A pentagon is a polygon with five sides and five angles. It is a closed, two-dimensional shape that is formed by connecting five line segments end to end. The sides of a pentagon do not intersect each other. The interior angles of a pentagon add up to a total of 540 degrees.
What is the Pentagon Shape?
The pentagon shape is a five-sided polygon with unique properties. It is distinct from other polygons, such as triangles or quadrilaterals, due to its specific number of sides and angles. The pentagon shape can be classified into different types based on the lengths of its sides, the measures of its angles, and the arrangement of its vertices.
The Shape of Pentagon
Regular Pentagon
A regular pentagon is a five-sided shape where all sides and angles are equal. Each interior angle measures 108 degrees, and each side is of the same length. The regular pentagon is both equilateral (having five equal sides) and equiangular (having five angles of equal measure).
Irregular Pentagon
An irregular pentagon, contrary to a regular pentagon, does not have all sides or angles equal, presenting an asymmetrical shape.
Convex Pentagon
A convex pentagon has all its vertices pointing outwards. None of the interior angles measure more than 180 degrees. A regular pentagon is an example of a convex pentagon.
Concave Pentagon
A concave pentagon is a five-sided figure with at least one interior angle greater than 180 degrees, which means at least one vertex points inward.
Equilateral Pentagons
An equilateral pentagon is a type of pentagon where all five sides are of equal length. However, unlike a regular pentagon, the angles in an equilateral pentagon do not need to be equal.
Cyclic Pentagons
A cyclic pentagon is a five-sided polygon in which all vertices lie on a common circle’s circumference. The vertices are concyclic, and the pentagon’s sides may have different lengths.
12 Kinds of Polygons
Polygons are diverse shapes with different numbers of sides and angles. Here are the twelve different types of polygons:
Triangle (three-sided polygon)
A triangle is a polygon with three sides and three angles. It is the simplest type of polygon.
Quadrilateral (four-sided polygon)
A quadrilateral is a polygon with four sides and four angles. Examples of quadrilaterals include rectangles, squares, parallelograms, and trapezoids.
Pentagon (five-sided polygon)
A pentagon is a polygon with five sides and five angles.
Hexagon (six-sided polygon)
A hexagon is a polygon with six sides and six angles.
Heptagon (seven-sided polygon)
A heptagon is a polygon with seven sides and seven angles.
Octagon (eight-sided polygon)
An octagon is a polygon with eight sides and eight angles.
Nonagon (nine-sided polygon)
A nonagon is a polygon with nine sides and nine angles.
Decagon (ten-sided polygon)
A decagon is a polygon with ten sides and ten angles.
Icosagon (twenty-sided polygon)
An icosagon is a polygon with twenty sides and twenty angles.
Triacontagon (thirty-sided polygon)
A triacontagon is a polygon with thirty sides and thirty angles.
Hectagon (100-sided polygon)
A hectagon is a polygon with one hundred sides and one hundred angles.
Chiliagon (1000-sided polygon)
A chiliagon is a polygon with one thousand sides and one thousand angles.

Geometrical Constructions
In geometry, there are various methods of constructing polygons with specific properties. Here are a few methods commonly used for constructing pentagons:
Richmond’s Method
Richmond’s method is a geometric construction technique used to construct a regular pentagon. It involves using a compass and straightedge to create the desired shape.
Carlyle Circles
Carlyle circles are a method of constructing a regular pentagon using a series of circles with specific radii. By intersecting these circles, a pentagon can be formed.
Euclid’s Method
Euclid’s method of constructing a regular pentagon involves a series of geometrical steps using a compass and straightedge. It is based on Euclid’s geometry principles and provides a precise way of constructing the shape.
Properties of a Pentagon
A pentagon has several unique properties that distinguish it from other polygons:
- A pentagon has five sides and five angles.
- The sum of the interior angles of a pentagon is always 540 degrees.
- In a regular pentagon, all five sides and angles are equal in measure.
- A regular pentagon has five lines of symmetry.
- The perimeter of a pentagon is the total distance around its five sides.
- The area of a pentagon is the amount of space enclosed by its five sides.
Pentagon Formula
The formulas for finding the area and perimeter of a pentagon are essential in the study of this geometric shape.
What is the Area of a Pentagon?
The formula for finding the area of a pentagon depends on whether it’s a regular or irregular pentagon. For a regular pentagon with a known side and apothem (a line segment from the center of the pentagon perpendicular to a side), the formula is:
Area of Pentagon = A = 1/2 * Perimeter * Apothem
For an irregular pentagon, the area can be found by breaking the pentagon into triangles and finding the sum of their areas.
What is the Perimeter of the Pentagon?
The perimeter of a regular pentagon is simply five times the length of one side. For an irregular pentagon, the perimeter is the sum of the lengths of all its sides.
Pentagon Sides and Angles
A pentagon has five sides and five angles. In a regular pentagon, all sides and angles are equal. Each interior angle measures 108 degrees, and each exterior angle measures 72 degrees.

Parts of a Pentagon Shape
A pentagon shape has several distinct parts that contribute to its overall structure:
Side
A side is one of the five line segments that form the perimeter of the pentagon. Each side connects two consecutive vertices of the shape.
Vertex
A vertex is a point where two sides of the pentagon meet. There are five vertices in a pentagon, and they form the corners of the shape.
Diagonal
A diagonal is a line segment that connects two non-adjacent vertices of the pentagon. A pentagon has five diagonals, and they create internal triangles within the shape.
Interior Angle
An interior angle is the angle formed by two consecutive sides of the pentagon on the inside of the shape. A regular pentagon has five interior angles, each measuring 108 degrees.
Symmetry
A pentagon can possess lines of symmetry, which are lines that divide the shape into two equal halves. A regular pentagon has five lines of symmetry, passing through its center and connecting opposite sides.
Frequently Asked Questions About Pentagon Shapes
How many sides does a pentagon have?
A pentagon has five sides. The word “penta” in its name refers to the number five.
Solved Examples on Pentagon Shapes
Let’s solve a couple of examples related to pentagon shapes to better understand their properties and calculations.
Example 1:
Find the area and perimeter of a regular pentagon whose side is 5 cm and apothem length is 6 cm.
Area of Pentagon = 1/2 * Perimeter * Apothem = 1/2 * 5 * 5 * 6 = 75 cm²
Perimeter of Pentagon = 5 * Side = 5 * 5 = 25 cm
Therefore, the area of the pentagon is 75 cm², and its perimeter is 25 cm.
Example 2:
Find the area and perimeter of a regular pentagon whose side is 4 cm and apothem length is 8 cm.
Area of Pentagon = 1/2 * Perimeter * Apothem = 1/2 * 5 * 4 * 8 = 80 cm²
Perimeter of Pentagon = 5 * Side = 5 * 4 = 20 cm
Therefore, the area of the pentagon is 80 cm², and its perimeter is 20 cm.
How Kunduz Can Help You Learn Pentagon Shapes?
At Kunduz, we understand the importance of learning and mastering geometric shapes like the pentagon. Our comprehensive learning materials, including interactive tutorials, practice exercises, and real-life examples, are designed to make learning enjoyable and effective. Whether you are a student or a teacher, Kunduz provides the resources you need to understand and excel in geometry. Join us today and embark on a journey of mathematical discovery!
For readers exploring the properties of pentagon and interested in a broader understanding of polygons, we offer various other polygon pages. These resources delve into the formulas, characteristics, and classifications of polygons, providing a comprehensive exploration of geometric shapes beyond the pentagon:
What is Quadrilateral? Properties, Definition, Types, Area, Solved Examples, FAQs
What is a Heptagon: Definition, Properties, Types, Formula, Solved Example
Octagon Shape: Definition, Properties, Formula, Examples, Sides & Angles