In the realm of geometry, the concept of a perpendicular bisector holds great significance. It is a line or line segment that intersects another line or line segment perpendicularly, dividing it into two equal parts. The perpendicular bisector plays a crucial role in various geometric constructions, calculations, and proofs. Understanding the definition, properties, construction, and examples of perpendicular bisectors is essential for mastering geometry concepts.
What is the Perpendicular Bisector?
A perpendicular bisector is a line or line segment that divides another line segment into two equal parts and intersects it at a right angle. It is characterized by its ability to cut a line segment through its midpoint, resulting in two congruent segments. The term “bisect” refers to dividing equally, and when combined with “perpendicular,” it denotes a line that divides another line into two equal halves at a right angle.

How to Construct a Perpendicular Bisector?
Constructing a perpendicular bisector requires a ruler, compass, and pencil. Follow these steps to construct a perpendicular bisector for a given line segment:
Step 1: Draw a line segment, AB, of any desired length.
Step 2: Adjust the compass to a length slightly longer than half the length of AB.
Step 3: Place the compass pointer at point A and draw an arc above and below the line segment.
Step 4: Repeat the previous step by placing the compass pointer at point B and drawing arcs above and below the line segment.
Step 5: Mark the points of intersection of the arcs as P and Q.
Step 6: Use a ruler to draw a line passing through points P and Q. This line is the perpendicular bisector of the line segment AB.
The perpendicular bisector divides the line segment AB into two equal parts, and the angle formed between the two line segments is 90 degrees.
Perpendicular Bisector of Triangles
The perpendicular bisector of a triangle is a line segment that bisects the sides of the triangle and is perpendicular to the sides. It divides each side into two equal parts and passes through the midpoint of each side. A triangle has three perpendicular bisectors, one for each side. The point at which all three perpendicular bisectors intersect is called the circumcenter of the triangle. The circumcenter is equidistant from all three vertices of the triangle.

Perpendicular Bisector Theorem
The Perpendicular Bisector Theorem states that if a point lies on the perpendicular bisector of a line segment, it is equidistant from the endpoints of the segment. In other words, the distance from the point to each endpoint is the same. This theorem is a fundamental concept in geometry and is often used in proofs and calculations.
Proof of Perpendicular Bisector Theorem
To prove the Perpendicular Bisector Theorem, consider a line segment AB and a point P on the perpendicular bisector of AB. We need to show that the distance from P to A is equal to the distance from P to B.
Let’s assume that P is equidistant from both A and B. This means that PA = PB. Now, draw lines connecting P to A and P to B.
In triangle PAB, we have PA = PB (given), and the side PA is congruent to the side PB. Additionally, the angles PAB and PBA are congruent since they are vertical angles.
By the Side-Angle-Side (SAS) congruence criterion, we can conclude that triangle PAB is congruent to triangle PBA.
Therefore, the corresponding angles PAB and PBA are congruent, and the corresponding sides PA and PB are congruent.
Since the two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, we can conclude that triangle PAB is congruent to triangle PBA.
As a result of this congruence, the angles APB and BPA are congruent.
Since the angles APB and BPA are congruent, they must each measure 90 degrees, as the sum of the angles in a triangle is 180 degrees.
Therefore, we have shown that the point P lies on the perpendicular bisector of AB, and the distance from P to A is equal to the distance from P to B.
Hence, we have proved the Perpendicular Bisector Theorem.
Converse of the Perpendicular Bisector Theorem
The converse of the Perpendicular Bisector Theorem states that if a point is equidistant from the endpoints of a line segment, it lies on the perpendicular bisector of that segment.
To prove the converse, assume that a point P is equidistant from the endpoints A and B of a line segment AB. This means that the distances PA and PB are equal.
Now, draw lines connecting P to A and P to B. In triangle PAB, we have PA = PB (given), and the side PA is congruent to the side PB.
Additionally, we can conclude that the angles PAB and PBA are congruent since they are vertical angles.
By the Side-Angle-Side (SAS) congruence criterion, we can conclude that triangle PAB is congruent to triangle PBA.
Therefore, the corresponding angles PAB and PBA are congruent, and the corresponding sides PA and PB are congruent.
Since the two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, we can conclude that triangle PAB is congruent to triangle PBA.
As a result of this congruence, the angles APB and BPA are congruent.
Since the angles APB and BPA are congruent, they must each measure 90 degrees, as the sum of the angles in a triangle is 180 degrees.
Therefore, we have shown that the point P lies on the perpendicular bisector of AB.
Hence, we have proved the converse of the Perpendicular Bisector Theorem.
Perpendicular Bisector of a Line Segment
A perpendicular bisector can also be constructed for a line segment. The process is similar to the construction of a perpendicular bisector for a triangle.
To construct a perpendicular bisector for a line segment AB, follow these steps:
- Draw the line segment AB of any desired length.
- With a compass and more than half the length of AB as the radius, draw arcs above and below the line segment from point A.
- Without changing the radius of the compass, repeat the previous step from point B.
- Label the points of intersection of the arcs as P and Q.
- Use a ruler to draw a line passing through points P and Q. This line is the perpendicular bisector of the line segment AB.
The perpendicular bisector divides the line segment AB into two equal parts, and the angle formed between the two line segments is 90 degrees.
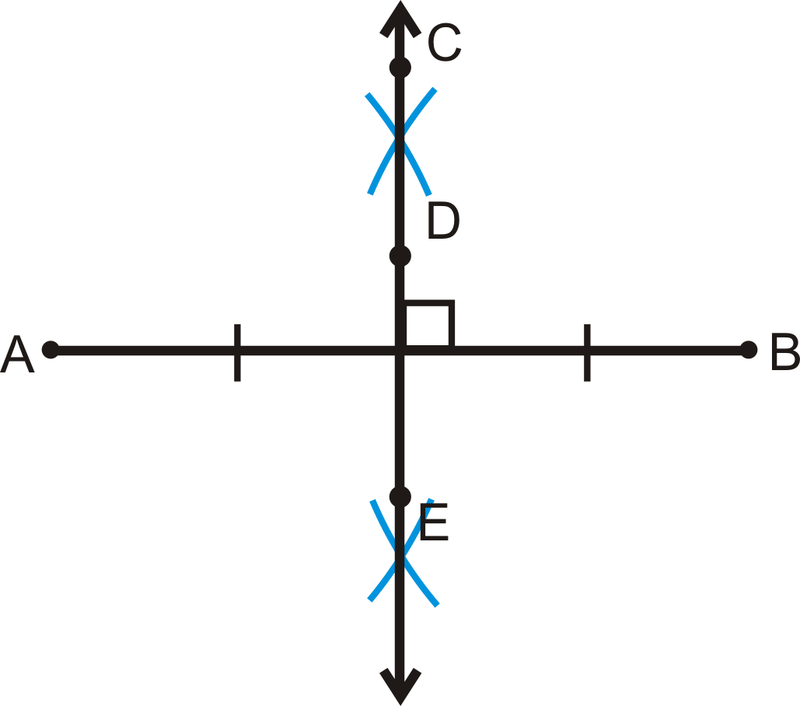
Graphical Representation of a Perpendicular Bisector
A perpendicular bisector can be represented graphically by drawing a line or line segment that is perpendicular to the original line segment and passes through its midpoint. The perpendicular bisector intersects the original line segment at a right angle, dividing it into two equal parts.
This graphical representation of a perpendicular bisector is often depicted as a dashed line with a right angle symbol at the point of intersection.
Equation of a Perpendicular Bisector
The equation of a perpendicular bisector can be determined using the midpoint formula and the slope formula.
The midpoint formula is used to find the midpoint of a line segment. If the coordinates of the endpoints of the line segment are (x1, y1) and (x2, y2), the midpoint is given by:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
The slope formula is used to find the slope of a line segment. If the coordinates of the endpoints of the line segment are (x1, y1) and (x2, y2), the slope is given by:
Slope = (y2 – y1)/(x2 – x1)
To find the slope of the perpendicular bisector, take the negative reciprocal of the slope of the original line segment. The negative reciprocal of a number is obtained by changing its sign and flipping it upside down. For example, if the slope of the original line segment is m, the slope of the perpendicular bisector is -1/m.
Once the midpoint and the slope of the perpendicular bisector are determined, the equation of the line can be written using the point-slope form, which is:
y – y1 = m(x – x1)
where (x, y) is a point on the perpendicular bisector, (x1, y1) is the midpoint, and m is the slope of the perpendicular bisector.
Perpendicular Bisector of a Chord
In the context of circles, a perpendicular bisector of a chord is a line or line segment that is perpendicular to the chord and passes through its midpoint. The perpendicular bisector of a chord also passes through the center of the circle.
The perpendicular bisector of a chord divides the chord into two equal parts and is perpendicular to it at the midpoint. This property is useful in solving various circle-related problems and constructions.
Properties of Perpendicular Bisector
- A perpendicular bisector divides a line or line segment into two congruent segments.
- It forms a 90-degree angle with the line or line segment it bisects.
- Points on the perpendicular bisector are equidistant from the endpoints of the line or line segment.
- The intersection of the perpendicular bisectors of a triangle is called the circumcenter of the triangle.
- In an acute triangle, the circumcenter lies inside the triangle.
- In an obtuse triangle, the circumcenter lies outside the triangle.
- In a right triangle, the circumcenter lies on the hypotenuse.
- There can only be one perpendicular bisector for a given line or line segment.
Solved Examples on Perpendicular Bisector
Example 1: Find the equation of the perpendicular bisector of the line segment with endpoints (1, 2) and (5, 6).
Solution:
Step 1: Find the midpoint of the line segment using the midpoint formula. Midpoint = ((1 + 5)/2, (2 + 6)/2) = (3, 4)
Step 2: Find the slope of the line segment using the slope formula. Slope = (6 – 2)/(5 – 1) = 4/4 = 1
Step 3: Take the negative reciprocal of the slope to find the slope of the perpendicular bisector. Slope of the perpendicular bisector = -1/1 = -1
Step 4: Use the midpoint and the slope to write the equation of the perpendicular bisector in point-slope form. y – 4 = -1(x – 3) y – 4 = -x + 3 y = -x + 7
The equation of the perpendicular bisector is y = -x + 7.
Example 2: Construct the perpendicular bisector of the line segment with endpoints (2, 3) and (6, 1).
Solution: Follow the steps for constructing a perpendicular bisector:
- Draw the line segment with endpoints (2, 3) and (6, 1).
- Find the midpoint using the midpoint formula. Midpoint = ((2 + 6)/2, (3 + 1)/2) = (4, 2)
- Use a compass and the midpoint as the center to draw arcs above and below the line segment.
- Without changing the compass width, repeat the previous step with the other endpoint as the center.
- Connect the points where the arcs intersect to form the perpendicular bisector.
The constructed line is the perpendicular bisector of the line segment.
How Kunduz Can Help You Learn Perpendicular Bisectors?
If you find yourself struggling to understand the concept of perpendicular bisectors or any other geometry topic, Kunduz is here to help. Kunduz offers a comprehensive range of online math courses and tutoring services that can aid in your understanding of perpendicular bisectors.
Our experienced tutors are available to answer your questions, provide step-by-step explanations, and assist you in mastering the concept of perpendicular bisectors.
Whether you need assistance with constructing perpendicular bisectors, understanding the properties, or solving example problems, Kunduz has you covered.
Don’t let perpendicular bisectors and geometry concepts intimidate you. With Kunduz, you can gain the confidence and knowledge needed to excel in math. Start your learning journey with Kunduz today and unlock your full mathematical potential.
