In the realm of geometry, perpendicular lines play a crucial role. These lines intersect each other at a 90-degree angle, forming what is known as a right angle. Perpendicular lines can be observed in various real-life scenarios, such as the corners of walls, the shape of a letter ‘L’, or the hands of a clock at 3 o’clock. Understanding the concept of perpendicular lines is fundamental to grasping geometric principles and solving mathematical problems.
This article aims to provide a comprehensive overview of perpendicular lines, including their definition, properties, formulas, and examples. We will explore the symbolism associated with perpendicular lines, examine how to draw them using different tools, and delve into the relationship between perpendicular and parallel lines. By the end of this article, you will have a solid understanding of perpendicular lines and their significance in geometry.
What is Perpendicular?
Before diving into the specifics of perpendicular lines, let’s first define what it means for two lines to be perpendicular. In geometry, a line is considered perpendicular to another line if the two lines intersect and form a right angle. A right angle measures 90 degrees and is denoted by a small square at the intersection of the lines. This square symbolizes the perpendicular relationship between the lines.
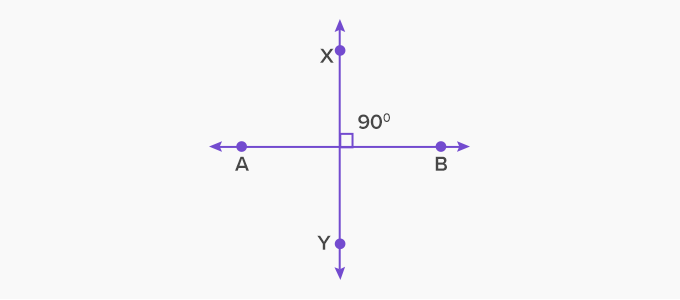
What are Perpendicular Lines?
Perpendicular lines are pairs of lines that intersect each other at a right angle. They can be lines, segments, or rays. The defining characteristic of perpendicular lines is the 90-degree angle formed at their point of intersection. This angle is known as a right angle and represents a quarter of a complete revolution.
To denote the perpendicular relationship between two lines, we use the symbol ⊥. For example, if line AB is perpendicular to line CD, we would express it as AB ⊥ CD. This symbol visually represents the right angle formed at the intersection of the lines.
Perpendicular Sign
The symbol ⊥ is used to represent perpendicular lines. It signifies that two lines intersect at a right angle. This symbol is placed between the two lines to indicate their perpendicular relationship. For instance, if line m is perpendicular to line n, we would write it as m ⊥ n.

Perpendicular Shapes
Perpendicular lines can be observed in various shapes, which are characterized by having at least two sides that meet at a right angle. Some common examples of perpendicular shapes include:
- Square: All four sides of a square are perpendicular to each other, forming right angles at their intersections.
- Rectangle: The opposite sides of a rectangle are parallel and perpendicular to each other.
- Right-angled Triangle: One of the angles in a right-angled triangle measures 90 degrees, making it perpendicular to one of the sides.
Understanding the concept of perpendicular shapes can help in identifying and analyzing geometric figures in real-world scenarios.
Perpendicular Lines Formula
The relationship between the slopes of two perpendicular lines can be described using a formula. Suppose we have two lines, line AB and line CD, and we want to determine if they are perpendicular to each other. We can use the slope formula to calculate the slopes of the lines and then apply the perpendicular lines formula.
The perpendicular lines formula states that the product of the slopes of two perpendicular lines is always -1. Mathematically, this can be expressed as:
m1 * m2 = -1
Where m1 and m2 are the slopes of the two lines. If the product of the slopes is -1, then the lines are perpendicular to each other.
It’s important to note that this formula applies specifically to lines in a two-dimensional plane. In three dimensions, the concept of perpendicularity expands to include three lines that are mutually perpendicular to each other.
Perpendicular Line Equation
To find the equation of a line perpendicular to a given line, we can use the concept of slope. The slope of a line is defined as the ratio of the change in y-coordinates to the change in x-coordinates. If we have the equation of a line in the form Ax + By + C = 0, we can determine the equation of a line perpendicular to it by following these steps:
- Find the slope of the given line by rearranging the equation in the form y = mx + b, where m represents the slope.
- Determine the negative reciprocal of the slope obtained in step 1. This can be done by flipping the fraction and changing its sign.
- Use the negative reciprocal slope as the slope in the equation of the perpendicular line.
- Choose a point on the given line and substitute the coordinates of that point into the equation of the perpendicular line.
- Solve for the y-intercept by substituting the values obtained in step 4 into the equation y = mx + b.
The resulting equation will represent a line that is perpendicular to the given line.
Properties of Perpendicular Lines
Perpendicular lines possess several properties that are worth exploring. By understanding these properties, we can gain further insight into the nature of perpendicular lines and their behavior. Some key properties of perpendicular lines include:
- Perpendicular lines always intersect each other at a right angle. This property is fundamental to the definition of perpendicularity.
- If two lines are perpendicular to the same line, they are parallel to each other and will never intersect. This property highlights the relationship between perpendicular and parallel lines.
- The adjacent sides of a square and the opposite sides of a rectangle are always perpendicular to each other. This property is specific to these two shapes.
- In a right-angled triangle, the sides enclosing the right angle are perpendicular to each other. This property helps in identifying right angles within triangles.
Understanding these properties can aid in problem-solving and geometric analysis, as they provide a framework for identifying and working with perpendicular lines.
How to Draw Perpendicular Lines?
Drawing perpendicular lines can be accomplished using various tools, such as a protractor or a compass. These tools help ensure accuracy and precision in creating perpendicular lines. Let’s explore two common methods for drawing perpendicular lines: using a protractor and using a compass.
Drawing a Perpendicular Line Using a Protractor
To draw a perpendicular line using a protractor, follow these steps:
- Begin with a given line, referred to as the base line.
- Place the protractor on the base line, aligning its base line with the base line of the given line. The center of the protractor should coincide with a point on the base line.
- Locate the 90-degree mark on the protractor and mark a point on the base line corresponding to this mark.
- Draw a line passing through the point marked in step 3, extending it beyond the base line.
- The line drawn in step 4 is perpendicular to the base line and can be used to form a right angle.
Using a protractor provides a straightforward method for drawing perpendicular lines with precision.

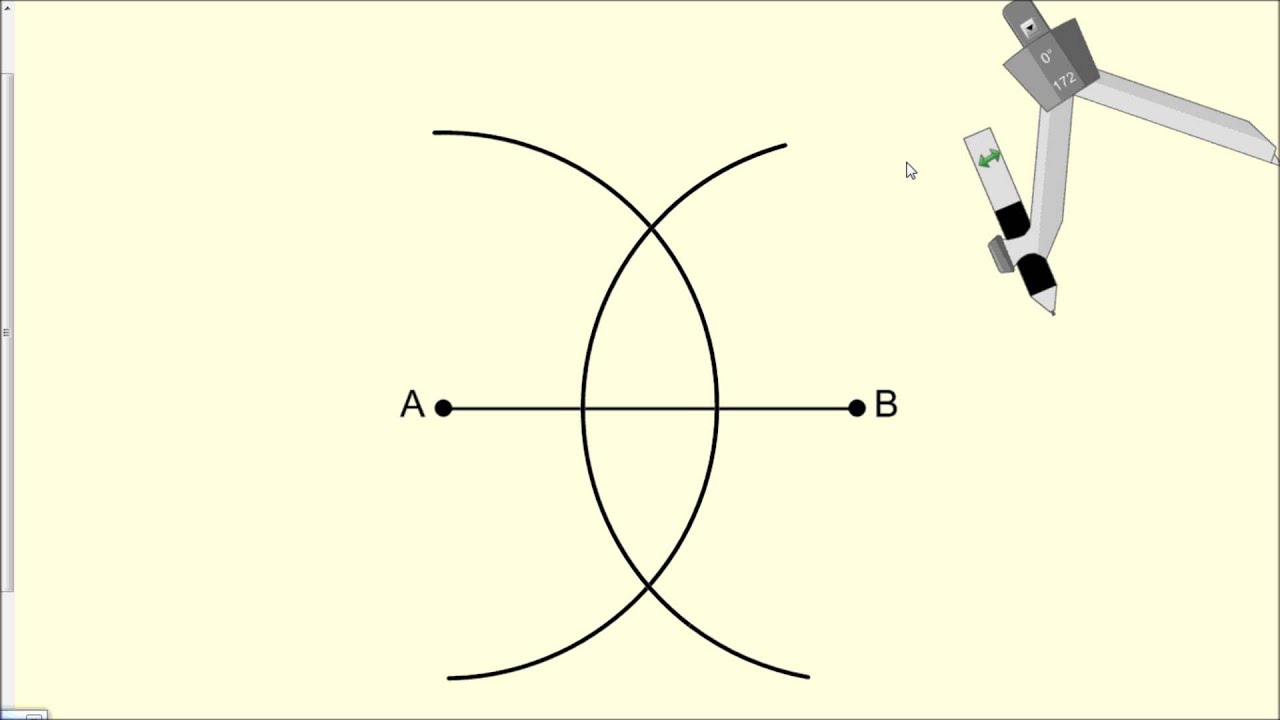
Drawing a Perpendicular Line Using a Compass
To draw a perpendicular line using a compass, follow these steps:
- Begin with a given line, referred to as the base line.
- Place the needle of the compass on any point along the base line.
- Adjust the compass to a desired radius.
- Draw an arc on one side of the base line, using the compass to maintain a consistent radius.
- Without changing the radius, place the needle of the compass on the other end of the base line and draw another arc on the same side as the previous arc.
- The two arcs should intersect. Connect the point of intersection with the point on the base line where the compass needle was initially placed.
- The line drawn in step 6 is perpendicular to the base line and forms a right angle at the intersection.
Using a compass allows for greater accuracy in drawing perpendicular lines, as it enables the creation of precise arcs.
Perpendicular and Parallel Lines
Perpendicular and parallel lines are distinct geometric concepts that are often studied together due to their contrasting characteristics. While perpendicular lines intersect at a right angle, parallel lines never intersect. Understanding the relationship between perpendicular and parallel lines is essential to comprehending geometric relationships and solving mathematical problems.
If two lines are perpendicular to the same line, they are parallel to each other. This property showcases the connection between perpendicular and parallel lines. For example, if line AB is perpendicular to line CD and line EF is also perpendicular to line CD, then line AB and line EF are parallel to each other.
It’s important to note that parallel lines are equidistant from each other and can be thought of as “running side by side” without ever intersecting. In contrast, perpendicular lines intersect at a right angle, forming a 90-degree angle at the point of intersection.
Understanding the distinction between perpendicular and parallel lines helps in analyzing geometric figures, identifying relationships, and solving mathematical problems involving line segments, angles, and shapes.
Difference Between Parallel and Perpendicular Lines
Parallel lines and perpendicular lines differ in several key aspects. Let’s examine the main differences between these two types of lines:
| Parallel Lines | Perpendicular Lines |
|---|---|
| Never intersect | Always intersect |
| Equidistant | Not equidistant |
| Example: Tracks of a railway line, opposite sides of a rectangle. | Example: Corners of a square, intersecting roads at a cross junction. |
Parallel lines are lines that never intersect. They are always equidistant from each other, maintaining the same distance throughout their length. This concept can be visualized as two train tracks running alongside each other without ever meeting.
On the other hand, perpendicular lines always intersect at a right angle, forming a 90-degree angle at the point of intersection. They are not equidistant, as the distance between them varies depending on their position.
The symbol used to represent parallel lines is $\parallel$, while the symbol used to represent perpendicular lines is $\perp$. These symbols visually indicate the nature of the lines and their relationship to each other.
Understanding the distinction between parallel and perpendicular lines enables us to recognize and analyze geometric relationships and solve mathematical problems effectively.
Slope of Perpendicular Lines
The slope of a line is a measure of its steepness or inclination. It is defined as the ratio of the change in y-coordinates to the change in x-coordinates. Perpendicular lines exhibit a specific relationship when it comes to their slopes.
If we have two lines, line AB and line CD, and we want to determine if they are perpendicular to each other, we can calculate their slopes using the slope formula. If the slopes of the two lines are negative reciprocals of each other, then the lines are perpendicular.
Mathematically, the relationship between the slopes of perpendicular lines can be expressed as:
m1 * m2 = -1
Where m1 and m2 represent the slopes of the two lines. If the product of the slopes is -1, then the lines are perpendicular to each other.
Understanding the relationship between the slopes of perpendicular lines is useful in determining perpendicularity and solving problems involving intersecting lines.
What is the Perpendicular Symbol?
In mathematics, the symbol that denotes perpendicularity is ‘⊥’. This symbol is used to express the relationship between two lines that intersect at a right angle. For instance, if line A is perpendicular to line B, it would be denoted as A ⊥ B.
The perpendicular symbol serves as a concise way to communicate the perpendicular relationship between lines, segments, or rays. It emphasizes the right angle formed at the point of intersection and is widely used in geometry and mathematics.
Do Perpendicular Lines Touch Each Other?
Yes, perpendicular lines intersect and touch each other at a single point. The point of intersection is referred to as the foot of the perpendicular. This intersection forms a right angle, with each line making a 90-degree angle with the other.
The concept of perpendicular lines is closely tied to the notion of intersecting lines, as perpendicular lines are a specific type of intersecting lines. Unlike parallel lines, which never intersect, perpendicular lines always intersect at a right angle.
Understanding that perpendicular lines touch each other at a single point is fundamental to comprehending their properties and applications in geometry.
How Do You Know If Two Lines Are Perpendicular?
Determining if two lines are perpendicular to each other requires identifying the relationship between their slopes. If the slopes of two lines are negative reciprocals of each other, then the lines are perpendicular.
To determine the slope of a line, we use the formula:
slope = (change in y-coordinates) / (change in x-coordinates)
If line AB has a slope of m1 and line CD has a slope of m2, we can apply the perpendicular lines formula:
m1 * m2 = -1
If the product of the slopes is -1, then the lines are perpendicular. This relationship arises due to the geometric property that perpendicular lines intersect at a right angle, forming a 90-degree angle at the point of intersection.
By calculating the slopes of two lines and examining their relationship, we can determine whether they are perpendicular to each other.
Are Diagonals of a Rhombus Perpendicular to Each Other?
Yes, the diagonals of a rhombus are always perpendicular to each other. A rhombus is a quadrilateral with all sides of equal length. Its diagonals connect opposite vertices, intersecting at a point inside the rhombus.
The diagonals of a rhombus intersect at a right angle, forming a 90-degree angle at the point of intersection. This property is true for all rhombi, regardless of the size or proportions of the shape.
Understanding the perpendicularity of the diagonals in a rhombus is essential in analyzing the properties and relationships within this geometric figure.
What is a Perpendicular Triangle?
A perpendicular triangle, also known as a right-angled triangle, is a triangle that contains one angle measuring 90 degrees. In other words, it has a right angle. The side opposite the right angle is known as the hypotenuse, while the other two sides are referred to as the legs.
The relationship between the sides of a right-angled triangle is governed by the Pythagorean theorem, which states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. This theorem provides a fundamental tool for solving problems involving right-angled triangles.
Understanding the properties and characteristics of right-angled triangles, including their perpendicular angle, is crucial in geometry and trigonometry.

Solved Examples On Perpendicular Lines
Let’s solve a few examples to further illustrate the concept and application of perpendicular lines.
Example 1: Determine if the lines with equations 3x + 2y + 5 = 0 and 2x – 3y + 8 = 0 are perpendicular.
Solution: We can determine the slopes of the lines by rearranging the equations in the form y = mx + b, where m represents the slope.
For the first equation, 3x + 2y + 5 = 0, we can rewrite it as y = (-3/2)x – 5/2. Thus, the slope of the first line is -3/2.
For the second equation, 2x – 3y + 8 = 0, we can rewrite it as y = (2/3)x + 8/3. Therefore, the slope of the second line is 2/3.
To determine if the lines are perpendicular, we can apply the perpendicular lines formula:
m1 * m2 = -1
Substituting the slopes into the formula, we have (-3/2) * (2/3) = -1. Since the product of the slopes is -1, we can conclude that the lines are perpendicular to each other.
Example 2: Find the equation of a line perpendicular to the line x + 2y + 5 = 0 and passing through the point (2, 5).
Solution: We can determine the equation of the perpendicular line by following these steps:
- Find the slope of the given line by rearranging the equation in the form y = mx + b. In this case, we have 2y = -x – 5, which simplifies to y = (-1/2)x – 5/2. Thus, the slope of the given line is -1/2.
- Determine the negative reciprocal of the slope obtained in step 1. In this case, the negative reciprocal of -1/2 is 2.
- Use the negative reciprocal slope as the slope in the equation of the perpendicular line. We now have y = 2x + b.
- Substitute the coordinates of the given point (2, 5) into the equation of the perpendicular line. We have 5 = 2(2) + b, which simplifies to 5 = 4 + b. Solving for b, we find that b = 1.
- The equation of the perpendicular line passing through the point (2, 5) is y = 2x + 1.
By following these steps, we can determine the equation of a line perpendicular to a given line and passing through a specific point.
How Kunduz Can Help You Learn Perpendicular?
At Kunduz, we understand the importance of a solid foundation in mathematics and geometry. We strive to provide comprehensive learning materials and resources to help students grasp fundamental concepts such as perpendicular lines.
Through our user-friendly platform, you can access a wealth of educational content, including interactive lessons, practice exercises, and step-by-step solutions. Our experienced math and physics teachers are dedicated to guiding you through the intricacies of perpendicular lines and other mathematical concepts.
Whether you’re struggling to understand perpendicular lines or seeking to deepen your knowledge, Kunduz is here to support you. Our affordable and accessible platform ensures that quality education is within reach for all students.
Don’t let perpendicular lines intimidate you. With Kunduz, you can master this key geometric concept and excel in your mathematical journey. Let us be your companion in learning, empowering you to achieve academic success.
