When it comes to graphing lines on the coordinate plane, understanding different forms of linear equations is essential. One commonly used form is the point slope form. In this article, we will explore what point slope form is, how it is different from other forms like slope-intercept form, and how to use it to solve problems. By the end, you’ll have a clear understanding of point slope form and its applications.
What is the Point Slope Form?
Point slope form is a way to express the equation of a straight line using a given point on the line and its slope. The equation is represented as (y – y1) = m(x – x1), where (x1, y1) are the coordinates of the given point, and m is the slope of the line. This form allows us to find the equation of a line without knowing the y-intercept, making it particularly useful when only a point and slope are given.

What is Slope Intercept Form?
Before diving deeper into point slope form, let’s briefly review slope intercept form. Slope intercept form is another way to express the equation of a straight line. It is represented as y = mx + b, where m is the slope of the line and b is the y-intercept. Slope intercept form is useful when both the slope and y-intercept are known.
What is a Coordinate Plane?
To understand point slope form better, it’s important to have a clear understanding of a coordinate plane. A coordinate plane is a two-dimensional plane formed by two intersecting lines called the x-axis and y-axis. The x-axis represents the horizontal direction, and the y-axis represents the vertical direction. Each point on the coordinate plane is represented by an ordered pair (x, y), where x represents the distance from the y-axis (horizontally) and y represents the distance from the x-axis (vertically).
What is the Point Slope Form of a Straight Line?
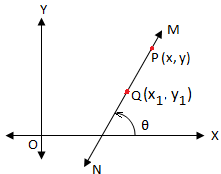
The point slope form of a straight line is an equation that represents a line passing through a given point (x1, y1) with a known slope, m. It is represented as (y – y1) = m(x – x1). This form allows us to find the equation of a line using a specific point and its slope. By substituting the values of the point and slope into the equation, we can determine the equation of the line.
Point Slope Formula
The point slope formula is the equation (y – y1) = m(x – x1) used to represent a line in point slope form. Let’s break down the formula:
- y and x: These variables represent the coordinates of any point on the line (x, y).
- y1 and x1: These variables represent the coordinates of the given point on the line (x1, y1).
- m: This variable represents the slope of the line.
By substituting the values of the point (x1, y1) and slope (m) into the formula, we can find the equation of the line in point slope form.
How to Solve Point Slope Form?
Solving point slope form involves finding the equation of a line using the given point and slope. Here’s a step-by-step guide on how to solve point slope form:
- Identify the slope (m) and the coordinates (x1, y1) of the given point on the line.
- Substitute the values of the slope and point into the point slope formula: (y – y1) = m(x – x1).
- Simplify and rearrange the equation, if necessary, to represent the line in point slope form.
By following these steps, you can solve point slope form problems and find the equation of a line.
Point Slope Form Formula of a Line In a Cartesian Plane
In a Cartesian plane, the point slope form formula represents the equation of a line using a given point and its slope. The formula is (y – y1) = m(x – x1), where (x1, y1) represents the coordinates of the given point, and m represents the slope of the line.
By substituting the values of the point and slope into the formula, we can determine the equation of the line in point slope form.
The Coefficients in Slope-Intercept Form
In slope-intercept form (y = mx + b), the coefficients have specific meanings. The coefficient of x (m) represents the slope of the line, indicating how steep or gradual the line is. The coefficient of y (1) indicates that y is multiplied by 1, meaning that it is not affected by any scaling. The constant term (b) represents the y-intercept, which is the point where the line intersects the y-axis.
Understanding the coefficients in slope-intercept form helps us interpret and analyze linear equations more effectively.
Derivation of Formula For Point Slope Form
The formula for point slope form, (y – y1) = m(x – x1), can be derived using the concept of slope. The slope of a line is defined as the change in y divided by the change in x between two points on the line. By considering the slope formula and using the coordinates of a given point (x1, y1), we can derive the point slope form formula.
The derivation involves setting up the slope equation, substituting the coordinates of the given point, and simplifying the equation to obtain the point slope form.
How to Find the Equation of a Line with Slope and Coordinates of a Point?
To find the equation of a line with a given slope and coordinates of a point, follow these steps:
- Identify the slope (m) and the coordinates (x1, y1) of the given point on the line.
- Substitute the values of the slope and point into the point slope formula: (y – y1) = m(x – x1).
- Simplify and rearrange the equation, if necessary, to represent the line in point slope form.
By following these steps, you can find the equation of a line using the slope and coordinates of a point.
Straight-Line Equation Using Point Slope Form
The point slope form provides a straightforward way to represent the equation of a straight line. By using the coordinates of a given point and its slope, we can determine the equation of the line using the point slope form formula: (y – y1) = m(x – x1).
This equation allows us to express the relationship between the x and y variables for any point on the line. By substituting the values into the equation, we can determine the equation of the line in point slope form.
Converting Point Slope Form to Slope Intercept Form
Converting point slope form to slope-intercept form (y = mx + b) is a common task in algebra. The slope-intercept form is often preferred because it explicitly shows the slope and y-intercept of the line.
To convert point slope form to slope-intercept form, follow these steps:
- Start with the point slope form equation: (y – y1) = m(x – x1).
- Distribute the slope (m) to the terms inside the parentheses.
- Simplify and rearrange the equation to isolate y on one side.
- Identify the y-intercept (b) from the simplified equation.
By following these steps, you can convert the equation from point slope form to slope-intercept form.
Converting Standard Form to Point Slope Form
Converting an equation from standard form (Ax + By = C) to point slope form ((y – y1) = m(x – x1)) can be helpful for visualizing the line’s slope and a specific point on the line.
To convert standard form to point slope form, follow these steps:
- Rewrite the equation in slope-intercept form (y = mx + b) by solving for y.
- Identify the slope (m) and y-intercept (b) from the slope-intercept form.
- Choose a point on the line (x1, y1).
- Use the point slope form formula: (y – y1) = m(x – x1) and substitute the values of m, x1, and y1.
- Simplify and rearrange the equation to obtain the point slope form.
By following these steps, you can convert an equation from standard form to point slope form and visualize the line’s slope and a specific point on the line.
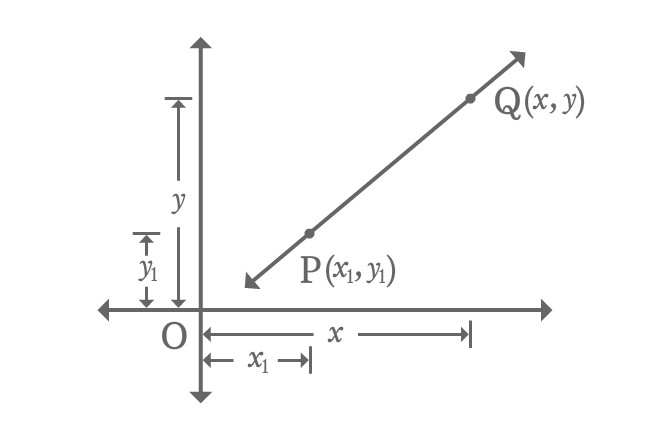
Point Slope Form Graph
Graphing a line in point slope form allows us to visualize the relationship between x and y variables. By using the slope and a specific point on the line, we can plot multiple points and connect them to form the line.
To graph a line in point slope form, follow these steps:
- Identify the slope (m) and the coordinates (x1, y1) of the given point on the line.
- Plot the given point (x1, y1) on the coordinate plane.
- Use the slope to find additional points by moving horizontally and vertically.
- Connect the points with a straight line to represent the line.
By following these steps, you can graph a line in point slope form and visualize its relationship on the coordinate plane.
Slope-Intercept and Point-Slope Forms of a Linear Equation
Slope-intercept form and point-slope form are two different ways to represent the equation of a linear equation.
Slope-intercept form (y = mx + b) is useful when the slope (m) and y-intercept (b) are known. It explicitly shows the slope of the line and the point where the line crosses the y-axis.
Point-slope form ((y – y1) = m(x – x1)) is useful when the slope (m) and a specific point (x1, y1) on the line are known. This form allows us to find the equation of the line without knowing the y-intercept.
Both forms have their advantages and are used in different situations depending on the available information about the line.
What is a Linear Equation?
A linear equation is an equation that represents a straight line in a coordinate plane. It is typically represented in the form y = mx + b, where m is the slope of the line and b is the y-intercept. Linear equations are used to model relationships between variables that have a constant rate of change.
Linear equations play a fundamental role in many fields, including mathematics, physics, engineering, and economics. They allow us to analyze and predict various phenomena and are essential tools for problem-solving.
Frequently Asked Questions About Point Slope Form
How do I calculate the intercept given point-slope form?
To calculate the y-intercept given the point-slope form equation (y – y1) = m(x – x1), you can rearrange the equation to solve for y. This will give you the equation in slope-intercept form (y = mx + b), where b represents the y-intercept.
What is the point slope formula with zero slope?
If the slope of a line is zero, the point-slope formula simplifies to (y – y1) = 0(x – x1), which can be further simplified to y – y1 = 0. This equation represents a horizontal line passing through the point (x1, y1).
Can point-slope form be the same as the slope-intercept form?
Point-slope form and slope-intercept form are two different ways to represent the equation of a line. While they convey the same information about the line, they have different forms. Point-slope form uses a specific point and slope, while slope-intercept form uses the slope and y-intercept.
What is the point slope form equation of a line passing through the origin with slope m?
If a line passes through the origin (0, 0) and has a slope of m, the point-slope form equation simplifies to y – 0 = m(x – 0), which further simplifies to y = mx. This equation represents a line that passes through the origin with a slope of m.
Is y = mx + b Point slope form?
No, y = mx + b is not point slope form. It is actually slope-intercept form. Point slope form is represented as (y – y1) = m(x – x1), where (x1, y1) are the coordinates of a specific point on the line and m is the slope.
How do you find the slope for two points?
To find the slope between two points (x1, y1) and (x2, y2), you can use the slope formula: m = (y2 – y1) / (x2 – x1). This formula calculates the change in y divided by the change in x, which represents the slope of the line connecting the two points.
When can we use the point slope formula?
The point slope formula is used when you know the slope of a line and a specific point that it passes through. It allows you to find the equation of the line without knowing the y-intercept. This form is particularly useful when only a point and slope are given.
Solved Examples on Point Slope Form
Example 1: Parallel Lines
Let’s consider two parallel lines. Line A has a slope of 2 and passes through the point (3, 5). Line B is parallel to Line A and passes through the point (1, 8). Find the equation of Line B in point slope form.
To find the equation of Line B, we can use the point slope formula. The slope of Line B is also 2, and the given point is (1, 8). Using the point slope formula, we have:
(y – 8) = 2(x – 1)
This is the equation of Line B in point slope form.
Example 2: Perpendicular Lines
Now, let’s consider two perpendicular lines. Line C has a slope of 3 and passes through the point (2, 4). Line D is perpendicular to Line C and passes through the point (1, -2). Find the equation of Line D in point slope form.
To find the equation of Line D, we can use the point slope formula. The slope of Line D is the negative reciprocal of the slope of Line C, which is -1/3. The given point is (1, -2). Using the point slope formula, we have:
(y – (-2)) = -1/3(x – 1)
This is the equation of Line D in point slope form.
Example 3: Applications of Linear Functions
Linear functions, represented by equations in point slope form, have various applications in real-world scenarios. For example, they can be used to model the growth of a population over time, the depreciation of an asset, or the rate of change in a physical quantity.
Let’s consider an example where a company’s revenue is growing linearly over time. The revenue (y) can be represented as a function of the number of years (x) since the company started. Suppose the revenue in the first year is $100,000, and it increases by $20,000 per year. The equation in point slope form would be:
(y – 100,000) = 20,000(x – 1)
This equation represents the revenue growth of the company over time.
By using linear functions in point slope form, we can analyze and predict various real-world phenomena and make informed decisions based on the data.
How Kunduz Can Help You Learn Point Slope Form?
If you’re struggling to understand point slope form, Kunduz is here to help. Kunduz is an online learning platform that offers comprehensive math and physics courses. Our experienced tutors provide step-by-step guidance, practice problems, and interactive lessons to help you master point slope form and other mathematical concepts.
With Kunduz, you can learn at your own pace, access resources anytime, and receive personalized support whenever you need it. Our goal is to make math and physics accessible and enjoyable for all students.
Don’t let point slope form confuse you. Join Kunduz today and unlock your full potential in math and physics. We’re here to support you every step of the way.
