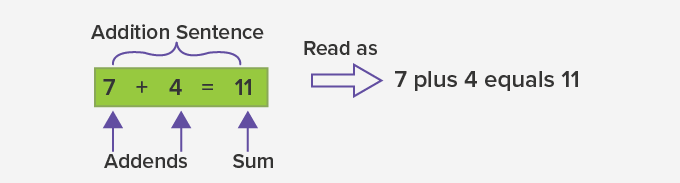
In mathematics, addition is a fundamental arithmetic operation that involves combining two or more numbers to find their sum. It is represented by the plus sign (+). The numbers that are being added are called addends, and the result is called the sum. Addition is an essential skill in various fields such as finance, engineering, and everyday life.
When performing addition, there are certain properties that govern the operation. These properties provide rules and guidelines that make addition easier to understand and manipulate. By understanding these properties, we can simplify complex calculations and solve mathematical problems more efficiently.
In this article, we will explore the four key properties of addition: the commutative property, associative property, distributive property, and additive identity property. We will define each property, provide examples to illustrate their application, and discuss their significance in mathematical operations.
For those mastering the properties of addition and seeking a comprehensive understanding of mathematical operations, our division of fractions and subtracting fractions pages serve as valuable references. These resources delve into fundamental principles that enrich the broader context of mathematical operations, providing insights into fraction manipulation and arithmetic
What is Addition?
Addition is the process of combining two or more numbers to find their total or sum. It is one of the fundamental arithmetic operations, along with subtraction, multiplication, and division. Addition is used in various real-life situations, such as calculating prices, measuring quantities, and solving mathematical equations.
To perform addition, we start by writing down the numbers that we want to add, also known as the addends. We then add the digits from right to left, carrying over any excess values when necessary. The final result is the sum of the addends.
For example:
23
+ 15
-----
38
In this example, the addends are 23 and 15. Adding them together gives us a sum of 38.
What Are Addition Properties?
Addition properties are a set of rules or characteristics that govern the operation of addition. These properties define how numbers can be added together and provide guidelines for performing addition operations. Understanding and applying these properties can simplify calculations and solve complex mathematical problems.
The four key properties of addition are the commutative property, associative property, distributive property, and additive identity property. Let’s explore each property in detail.
Properties of Addition
Commutative Property
The commutative property of addition states that the order of the addends does not affect the sum. In other words, when adding two numbers, we can change the order of the addends without changing the result.
Mathematically, the commutative property can be expressed as:
A + B = B + A
where A and B are any two numbers.
For example:
2 + 3 = 3 + 2 = 5
In this example, we can see that regardless of the order in which we add the numbers, the sum remains the same.
The commutative property also applies to more than two numbers. For example:
2 + 3 + 4 = 4 + 3 + 2 = 9
In this case, we can change the order of the addends without changing the sum.
The commutative property is helpful in mental math and simplifying calculations. It allows us to rearrange numbers in a way that makes addition easier.
Associative Property
The associative property of addition states that the grouping of the addends does not affect the sum. In other words, when adding three or more numbers, we can group them in any way without changing the final result.
Mathematically, the associative property can be expressed as:
(A + B) + C = A + (B + C)
where A, B, and C are any three numbers.
For example:
(2 + 3) + 4 = 2 + (3 + 4) = 9
In this example, we can see that regardless of how we group the numbers, the sum remains the same.
The associative property allows us to regroup numbers to simplify calculations and make them easier to solve. It is particularly useful when adding a large number of addends.
Distributive Property
The distributive property of addition combines addition and multiplication. It states that multiplying a number by the sum of two other numbers is the same as multiplying the number by each addend and then adding the products together.
Mathematically, the distributive property can be expressed as:
A × (B + C) = A × B + A × C
where A, B, and C are any three numbers.
For example:
2 × (3 + 4) = 2 × 3 + 2 × 4 = 14
In this example, we can see that we can distribute the multiplication over the addition and then perform the addition separately.
The distributive property is a powerful tool in simplifying calculations involving both addition and multiplication. It allows us to break down complex expressions and solve them step by step.
Additive Identity Property
The additive identity property states that adding zero to any number does not change the value of the number. In other words, the sum of any number and zero is equal to the original number.
Mathematically, the additive identity property can be expressed as:
A + 0 = A
where A is any number.
For example:
7 + 0 = 7
In this example, we can see that adding zero to 7 does not change the value of 7.
The additive identity property is useful in simplifying calculations and solving equations. It allows us to perform addition without altering the original values.
Other Properties of Addition
In addition to the four key properties discussed above, there are a few other properties related to addition that are worth mentioning.
Property of Opposites
The property of opposites states that for every real number, there exists a unique number called its additive inverse or opposite. When the original number and its opposite are added together, the sum is zero.
For example:
5 + (-5) = 0
In this example, 5 and -5 are additive inverses of each other, and their sum is zero.
Sum of Opposite of Numbers
The sum of the opposites of two numbers is equal to the sum of the negatives of the numbers. In other words, if A and B are two numbers, their opposites (-A and -B) will have the same sum as the negatives of the numbers.
Mathematically, this property can be expressed as:
-(A + B) = (-A) + (-B)
where A and B are any two numbers.
For example:
-(3 + 7) = (-3) + (-7)
In this example, we can see that the sum of the opposites of 3 and 7 is equal to the sum of their negatives.
Additive Inverse Property of Addition
The additive inverse property states that for every real number, there exists a unique number called its additive inverse or opposite. When the original number and its opposite are added together, the sum is zero.
For example:
9 + (-9) = 0
In this example, 9 and -9 are additive inverses of each other, and their sum is zero.
These additional properties further expand our understanding of addition and provide additional tools for solving mathematical problems.
Property of Addition | Statement and Example
| Property | Statement | Example |
|---|---|---|
| Commutative Property | A + B = B + A | 2 + 3 = 3 + 2 |
| Associative Property | (A + B) + C = A + (B + C) | (2 + 3) + 4 = 2 + (3 + 4) |
| Distributive Property | A × (B + C) = A × B + A × C | 2 × (3 + 4) = 2 × 3 + 2 × 4 |
| Additive Identity Property | A + 0 = A | 7 + 0 = 7 |
| Property of Opposites | A + (-A) = 0 | 5 + (-5) = 0 |
| Sum of Opposite of Numbers | -(A + B) = (-A) + (-B) | -(3 + 7) = (-3) + (-7) |
| Additive Inverse Property | A + (-A) = 0 | 9 + (-9) = 0 |
Solved Examples on Properties of Addition
Example 1:
Find the sum of (-2) + 7 using the commutative property.
Solution: According to the commutative property, the order of the addends does not affect the sum. Therefore, (-2) + 7 is equal to 7 + (-2).
7 + (-2) = 5
Hence, the sum of (-2) + 7 is 5.
Example 2:
Using the associative property, find the sum of 4 + (6 + 3).
Solution: According to the associative property, the grouping of the addends does not affect the sum. Therefore, 4 + (6 + 3) is equal to (4 + 6) + 3.
(4 + 6) + 3 = 10 + 3 = 13
Hence, the sum of 4 + (6 + 3) is 13.
Example 3:
Apply the distributive property to find the sum of 3 × (7 + 2).
Solution: According to the distributive property, multiplying a number by the sum of two other numbers is the same as multiplying the number by each addend and then adding the products together. Therefore, 3 × (7 + 2) is equal to 3 × 7 + 3 × 2.
3 × 7 + 3 × 2 = 21 + 6 = 27
Hence, the sum of 3 × (7 + 2) is 27.
How Kunduz Can Help You Learn Properties of Addition?
Kunduz is a comprehensive online learning platform that provides interactive and engaging resources for learning mathematics, including properties of addition. Kunduz offers a wide range of educational materials, such as tutorials, practice exercises, and quizzes, to help students understand and apply the properties of addition.
By using Kunduz, you can access step-by-step explanations and examples that make learning properties of addition easy and enjoyable. The platform provides a personalized learning experience, allowing you to progress at your own pace and track your progress along the way.
Whether you are a student looking to improve your math skills or a teacher seeking additional resources for your classroom, Kunduz has the tools and support you need. Join Kunduz today and unlock the potential of your mathematical abilities.
