In the world of geometry and mathematics, the concept of a circle holds great significance. One of the fundamental elements of a circle is the radius. Understanding the radius and its formula is essential for solving various geometric problems and calculations. In this article, we will explore the definition of the radius, its formula, and provide step-by-step instructions on how to find the radius of a circle in different scenarios. We will also examine solved examples to illustrate the practical application of the radius formula.
An Introduction to Radius Formula
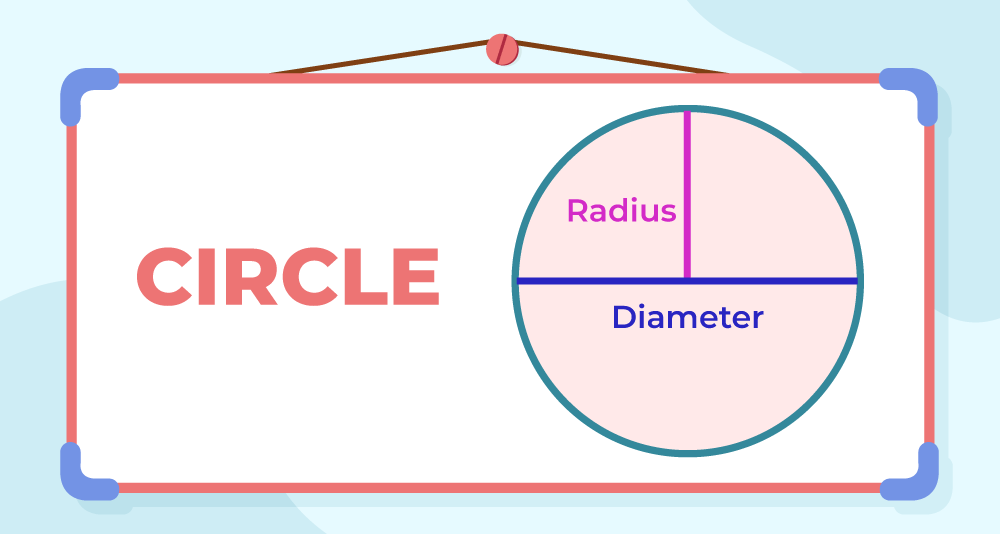
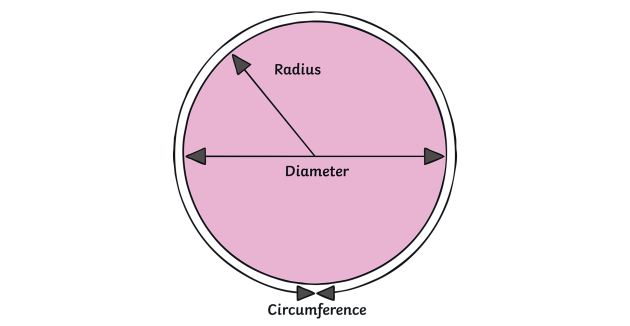
Before diving into the specifics of the radius formula, let’s first understand the concept of radius. The radius of a circle is defined as a straight line segment that connects the center of the circle to any point on its circumference. It is denoted by the letter ‘r’ and is crucial in determining the size and properties of a circle. The radius is half the length of the diameter, which is a line segment passing through the center of the circle and connecting two points on its circumference.
What is Radius?
The radius of a circle is a fundamental measurement that plays a significant role in geometry and mathematics. It represents the distance from the center of the circle to any point on its circumference. All radii of a circle are equal in length, as they connect the center to various points on the circumference. In simple terms, the radius defines the size of the circle and helps in calculating other important parameters such as the diameter, circumference, and area.
What is the Radius Formula?
The radius formula allows us to calculate the length of the radius when other parameters of a circle are known. There are different formulas to find the radius based on the given information. Let’s explore these formulas in detail.
Radius in Terms of Diameter
The diameter of a circle is the longest line segment that passes through the center and connects two points on the circumference. The radius is half the length of the diameter, and we can calculate the radius using the following formula:
Radius = Diameter/2
In mathematical terms, the radius formula in terms of the diameter can be expressed as:
Radius = √(Diameter/2)
Radius in Terms of Circumference
The circumference of a circle is the distance around its outer boundary. It is calculated using the formula C = 2πr, where ‘C’ represents the circumference and ‘r’ represents the radius. By rearranging the formula, we can find the radius when the circumference is known:
Radius = Circumference/2π
Radius in Terms of Area
The area of a circle is the amount of space enclosed within its boundaries. It is calculated using the formula A = πr², where ‘A’ represents the area and ‘r’ represents the radius. By rearranging the formula, we can find the radius when the area is known:
Radius = √(Area/π)
How to Find the Radius of a Circle?
Now that we understand the different formulas to find the radius, let’s explore step-by-step instructions on how to find the radius of a circle in various scenarios.
How to Find the Radius of a Circle When a Diameter is Given?
Step 1: Identify the given value of the diameter.
Step 2: Apply the radius formula in terms of the diameter: Radius = Diameter/2.
Step 3: Divide the given diameter by 2 to find the radius.
Let’s solve an example to illustrate the process:
Example 1: Find the radius of a circle whose diameter is 24 inches long.
Solution:
Step 1: Given diameter = 24 inches.
Step 2: Apply the radius formula: Radius = Diameter/2.
Step 3: Divide the diameter by 2: Radius = 24/2 = 12 inches.
Answer: The radius of the given circle is 12 inches.
How to Find the Radius of a Circle When Circumference is Given?
Step 1: Identify the given value of the circumference.
Step 2: Apply the radius formula in terms of the circumference: Radius = Circumference/2π.
Step 3: Divide the given circumference by 2π to find the radius.
Let’s solve an example to illustrate the process:
Example 2: Find the radius of a circle whose circumference is 4π units.
Solution:
Step 1: Given circumference = 4π units.
Step 2: Apply the radius formula: Radius = Circumference/2π.
Step 3: Divide the circumference by 2π: Radius = 4π/2π = 2 units.
Answer: The radius of the given circle is 2 units.
How to Find the Radius of a Circle When Area is Given?
Step 1: Identify the given value of the area.
Step 2: Apply the radius formula in terms of the area: Radius = √(Area/π).
Step 3: Take the square root of the given area divided by π to find the radius.
Let’s solve an example to illustrate the process:
Example 3: Find the radius of a circle whose area is 4π units².
Solution:
Step 1: Given area = 4π units².
Step 2: Apply the radius formula: Radius = √(Area/π).
Step 3: Take the square root of the area divided by π: Radius = √(4π/π) = 2 units.
Answer: The radius of the given circle is 2 units.
What is the Radius of the Circle that Passes Through Three Non-Collinear Points?
The radius of a circle that passes through three non-collinear points can be calculated using the following formula:
Radius = |O→X₁ - O→X₃| / (2 * Sin θ)
Here, O→X₁ and O→X₃ represent the vectors from the center of the circle to the respective points, and θ is the angle ∠X₁, X₂, X₃.
Radius of a Sphere
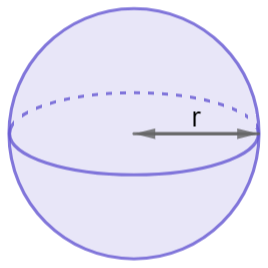
The concept of radius is not limited to circles alone. In three-dimensional geometry, a sphere also has a radius. The radius of a sphere is defined as the distance from the center of the sphere to any point on its surface. The radius of a sphere is denoted by ‘r’ and is crucial in determining the size and properties of the sphere.
Differences between Radius and Diameter
The terms radius and diameter are often used interchangeably, but they have distinct meanings in geometry. Let’s explore the differences between radius and diameter.
Radius:
- The radius is a straight line segment that connects the center of the circle or sphere to any point on its circumference or surface.
- The radius is half the length of the diameter.
- It is denoted by the letter ‘r’.
Diameter:
- The diameter is a straight line segment that passes through the center of the circle or sphere and connects two points on its circumference or surface.
- The diameter is twice the length of the radius.
- It is denoted by the letter ‘d’.
| Radius | Diameter |
|---|---|
| Represents the distance from the center of the circle or sphere to any point on its circumference or surface. | Represents the distance between two points on the circumference or surface of the circle or sphere, passing through the center. |
| Denoted by the letter ‘r’. | Denoted by the letter ‘d’. |
| Half the length of the diameter. | Twice the length of the radius. |
| Used to calculate other parameters such as circumference and area. | Used to calculate other parameters such as circumference and area. |
| The radius formula is used to find the length of the radius. | The diameter formula is used to find the length of the diameter. |
Solved Examples on Radius Formula
Let’s explore a few solved examples to further enhance our understanding of the radius formula.
Example 1: Given the diameter of a circle is 10 cm, find the radius.
Solution:
Step 1: Given diameter = 10 cm.
Step 2: Apply the radius formula: Radius = Diameter/2.
Step 3: Divide the diameter by 2: Radius = 10/2 = 5 cm.
Answer: The radius of the given circle is 5 cm.
Example 2: Find the radius of a circle whose circumference is 18π units.
Solution:
Step 1: Given circumference = 18π units.
Step 2: Apply the radius formula: Radius = Circumference/2π.
Step 3: Divide the circumference by 2π: Radius = 18π/2π = 9 units.
Answer: The radius of the given circle is 9 units.
Example 3: Find the radius of a circle whose area is 25π units².
Solution:
Step 1: Given area = 25π units².
Step 2: Apply the radius formula: Radius = √(Area/π).
Step 3: Take the square root of the area divided by π: Radius = √(25π/π) = 5 units.
Answer: The radius of the given circle is 5 units.
How Kunduz Can Help You Learn Radius Formula?
Understanding the concept of radius and its formula is crucial for excelling in geometry and mathematics. Through step-by-step explanations, Kunduz helps you build a strong foundation in geometry and mathematics. Whether you’re a beginner or looking to enhance your skills, Kunduz provides a conducive learning environment that fosters growth and understanding.
So, embark on your journey of learning and master the radius formula with Kunduz. Start today and unlock your full potential in geometry and mathematics.