The radius of a circle is a fundamental concept in geometry. It is defined as the distance from the center of the circle to any point on its circumference. The radius is denoted by the lowercase letter “r” and plays a crucial role in various circle-related formulas. Understanding the concept of radius is essential for solving problems involving circles and spheres.
An Introduction to the Radius of a Circle
In geometry, a circle is a closed curve consisting of all points in a plane that are equidistant from a fixed center point. The radius is a line segment that connects the center of the circle to any point on its circumference. It is important to note that all radii of a circle are equal in length.
What is Radius?
Radius, denoted as “r,” is the measurement of the distance between the center of a circle and any point on its circumference. It is half the length of the diameter of the circle. The diameter, denoted as “d,” is the longest chord of a circle, which is a line segment that connects two points on the circle’s circumference.
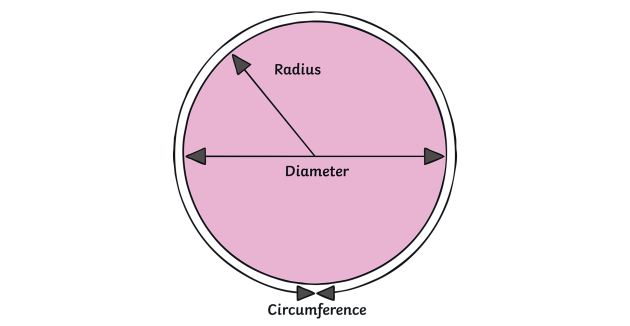
What is the Radius of a Circle?
The radius of a circle is a crucial parameter used to define and analyze circles. It is the distance from the center of the circle to any point on its circumference. The radius is key in determining the circumference, area, and other properties of a circle.
Radius of Circle Formulas
To calculate the radius of a circle, several formulas can be used depending on the given information. These formulas are derived based on the relationship between the radius, diameter, circumference, and area of a circle.
Radius Formula with Diameter
The diameter of a circle is twice the length of its radius. Therefore, the formula to find the radius from the diameter is:
Radius = Diameter / 2
Radius Formula from Circumference
The circumference of a circle is the distance around its perimeter. The formula to find the radius from the circumference is:
Radius = Circumference / (2 * π)
Here, π (pi) is a mathematical constant approximately equal to 3.14159.
Radius Formula using Area
The area of a circle is the measure of the space enclosed by its circumference. The formula to find the radius from the area is:
Radius = √(Area / π)
Where π (pi) is the mathematical constant approximately equal to 3.14159.
Radius of Circle Equation
The equation of a circle in the Cartesian coordinate system is given by (x − h)² + (y − k)² = r², where (h, k) is the center of the circle, and ‘r’ is the radius. This equation describes all the points (x, y) that lie on the circumference of the circle at a fixed distance ‘r’ from the center.
Properties of a Circle
A circle has several important properties that are related to its radius:
- All points on the circle’s circumference are equidistant from its center.
- The radius is perpendicular to any tangent line drawn from the center to the circle’s circumference.
- The radius bisects any chord of the circle that passes through its center.
Understanding these properties can help in solving problems involving circles and their various components.
Radius of a Circle
The radius is an essential component of a circle. It is the length between the center of the circle and any point on its circumference. A circle can have multiple radii, all of which are equal in length. The size of the circle changes as the length of the radius changes.
How to Find the Radius of a Circle?
To find the radius of a circle, you can use the following formulas based on the given information:
If the Diameter is Known
If the diameter of a circle is known, you can find the radius by dividing the diameter by 2. The formula to find the radius from the diameter is:
Radius = Diameter / 2
If the Circumference is Known
If the circumference of a circle is known, you can find the radius by dividing the circumference by 2π. The formula to find the radius from the circumference is:
Radius = Circumference / (2 * π)
If the Area is Known
If the area of a circle is known, you can find the radius by taking the square root of the area divided by π. The formula to find the radius from the area is:
Radius = √(Area / π)
Radius of a Sphere
A sphere is a three-dimensional object with all points on its surface equidistant from its center. The radius of a sphere is the distance from its center to any point on its surface. To calculate the radius of a sphere, you can use the formulas based on its volume or surface area.
Radius of a Sphere from Volume
The formula to find the radius of a sphere from its volume is:
Radius = ∛((3 * Volume) / (4 * π))
Where Volume represents the volume of the sphere and π is the mathematical constant approximately equal to 3.14159.
Radius of a Sphere from Surface Area
The formula to find the radius of a sphere from its surface area is:
Radius = √((Surface Area) / (4 * π))
Where Surface Area represents the surface area of the sphere and π is the mathematical constant approximately equal to 3.14159.
Parts of a Circle
A circle has several important components, including the radius, diameter, circumference, and area. Understanding these parts and their relationships is crucial for solving problems involving circles.
Radius, Diameter, and Chord
In a circle, the diameter is a line segment that passes through the center and divides the circle into two equal halves. The radius is a line segment that connects the center to any point on the circle’s circumference. A chord is a line segment that connects two points on the circle’s circumference. The diameter is twice the length of the radius, and any chord passing through the center of the circle is equal to the diameter.
Intersecting Lines
If a line intersects a circle at two distinct points, it is called a secant. A secant has two distinct chords associated with it, and the perpendicular line drawn from the center of the circle to the secant bisects both chords.
Tangent to a Circle
If a line touches a circle at exactly one point, it is called a tangent. A tangent line is always perpendicular to the radius drawn to the point of tangency.
Non-Intersecting Lines
If a line does not intersect a circle, it is called a non-intersecting line. Non-intersecting lines do not have any chord associated with them.
Circle Theorems
Circle theorems are mathematical principles that apply to circles and their components. These theorems help in understanding the properties and relationships of different parts of a circle. Some common circle theorems include:
- The perpendicular line drawn from the center of a circle to a chord bisects the chord.
- The line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
- The angles formed by two chords intersecting inside a circle are proportional to the lengths of the chords.
- The opposite angles formed by two intersecting chords inside a circle are equal.
Understanding these theorems can simplify problem-solving involving circles and their properties.
Frequently Asked Questions on Radius of a Circle
Where is the radius of a circle?
The radius of a circle is the line segment that connects the center of the circle to any point on its circumference.
Is a radius half of a diameter?
Yes, the radius of a circle is always half the diameter.
What is the formula to find the radius?
The radius can be calculated from the diameter (Radius = Diameter/2), circumference (Radius = Circumference/2π), or area (Radius = √(Area/π)).
How Many Radii can be drawn in a Circle?
An infinite number of radii can be drawn in a circle since there are infinite points on the circumference of a circle.
How to Find the Radius of a Circle?
The radius of a circle can be calculated if the diameter, circumference, or area of the circle is known, using the respective formulas.
Is it possible for the radius of the circle to be negative?
No, the radius of a circle cannot be negative. It’s a measure of distance, and hence, it’s always positive.
Can the radius of a circle be a fraction?
Yes, the radius of a circle can be a fraction. It’s a measure of length and can take any positive real value, including fractions.
Solved Examples on Radius of a Circle
Example 1: Find the radius of a circle whose diameter is 12 cm.
Solution: Given, Diameter of the circle = 12 cm Radius of the circle = Diameter / 2 = 12 / 2 = 6 cm
Example 2: If the circumference of a circle is 36 cm, find its radius.
Solution: Given, Circumference of the circle = 36 cm Radius of the circle = Circumference / (2 * π) = 36 / (2 * 3.14159) ≈ 5.73 cm
Example 3: Find the radius of a circle whose area is 154 sq. cm.
Solution: Given, Area of the circle = 154 sq. cm Radius of the circle = √(Area / π) = √(154 / 3.14159) ≈ 7 cm
How Kunduz Can Help You Learn Radius of a Circle?
At Kunduz, we understand the importance of mastering the concept of the radius of a circle. Our experienced math tutors are available to provide personalized assistance and guidance to help you understand and solve problems related to the radius of a circle. Whether you need help with calculations, formulas, or real-world applications, our tutors are here to support your learning journey. With Kunduz, learning the radius of a circle becomes an engaging and rewarding experience.
