Rational numbers are a fundamental concept in mathematics that plays a crucial role in various fields, including number theory, algebra, and calculus. In this comprehensive guide, we will delve into the world of rational numbers, exploring their definition, types, properties, and providing solved examples to enhance your understanding. We will also distinguish between rational and irrational numbers, shedding light on their key differences. So, let’s embark on this mathematical journey and unravel the mysteries of rational numbers!
An Introduction to Rational Numbers
In the vast realm of numbers, rational numbers hold a significant position. A rational number is defined as a number that can be expressed as the quotient or fraction of two integers, where the denominator is not equal to zero. In simpler terms, any fraction with a non-zero denominator can be classified as a rational number. For instance, 1/2, 1/5, and 3/4 are all examples of rational numbers. It’s important to note that the number zero is also considered a rational number, as it can be expressed in various forms, such as 0/1, 0/2, and so on.
What are Rational Numbers?
To delve deeper into the world of rational numbers, let’s understand their definition more explicitly. A rational number is a number that can be expressed in the form of p/q, where p and q are integers, and q is not equal to zero. For example, 2/3, -3/4, and 22/7 are all rational numbers. Rational numbers encompass a wide range of numbers, including integers, fractions, and terminating and repeating decimals. Thus, they form an extensive set that plays a crucial role in mathematical calculations and concepts.

What are Irrational Numbers?
While rational numbers encompass a vast range of numbers, there exists another category known as irrational numbers. Irrational numbers are those that cannot be expressed as fractions or ratios of integers. They are numbers that cannot be written in the form of p/q, where p and q are integers. Examples of irrational numbers include the square root of 2 (√2), the mathematical constant π (pi), the transcendental number e, and the golden ratio (φ). Unlike rational numbers, irrational numbers have decimal expansions that neither terminate nor repeat. It’s important to note that irrational numbers are a subset of real numbers, a larger set that encompasses both rational and irrational numbers.
How to Identify Rational Numbers?
Identifying whether a number is rational or not can be determined by a few key characteristics. To identify a rational number, consider the following:
- The number should be in the form of p/q, where q is not equal to zero.
- The fraction p/q should be reducible or convertible to decimal form.
- Rational numbers can be positive, negative, or zero.
- Non-terminating decimals that have repeating patterns (recurring decimals) can also be considered rational numbers.
By applying these criteria, you can easily determine if a number falls into the category of rational numbers.
How to Classify Rational and Irrational Numbers?
To understand the relationship between rational and irrational numbers, visualizing them using a Venn diagram can be helpful. In the diagram, the set of rational numbers and the set of irrational numbers are depicted as overlapping circles. The overlapping region represents the numbers that are both rational and irrational, which is essentially an empty set since a number cannot be both rational and irrational simultaneously.
The rational numbers include integers, fractions made up of integers, terminating decimal numbers, and non-terminating decimal numbers with infinitely repeating patterns. On the other hand, irrational numbers encompass numbers that cannot be expressed as fractions or ratios, such as the square root of 2 (√2), π (pi), and e.
Examples of Rational Numbers
To further illustrate the concept of rational numbers, let’s explore some examples:
- 36/3 = 12: This fraction can be simplified to its lowest terms, resulting in the whole number 12.
- 10011/100 = 100.11: This fraction converts to a decimal number with two decimal places.
- 11/99 = 0.111111…: This fraction represents a non-terminating decimal with a repeating pattern of 1s after the decimal point.
These examples demonstrate the diverse forms that rational numbers can take, including whole numbers, decimals, and recurring decimals.
Operations and Arithmetic on Rational Numbers
Rational numbers are not only essential in representing quantities but also in performing mathematical operations. Let’s explore the four fundamental arithmetic operations on rational numbers: addition, subtraction, multiplication, and division.
Addition of Rational Numbers
To add two rational numbers, we can follow the steps below:
- Find a common denominator for both fractions.
- Convert both fractions to equivalent fractions with the common denominator.
- Add the numerators of the equivalent fractions.
- Simplify the resulting fraction if possible.
For example, let’s add 1/2 and 2/3:
Step 1: Find the common denominator, which is 6.
Step 2: Convert 1/2 to an equivalent fraction with a denominator of 6: (1/2) × (3/3) = 3/6.
Step 3: Convert 2/3 to an equivalent fraction with a denominator of 6: (2/3) × (2/2) = 4/6.
Step 4: Add the numerators: 3/6 + 4/6 = 7/6.
The sum of 1/2 and 2/3 is 7/6.
Subtraction of Rational Numbers
Subtracting rational numbers follows a similar process to addition:
- Find a common denominator for both fractions.
- Convert both fractions to equivalent fractions with the common denominator.
- Subtract the numerators of the equivalent fractions.
- Simplify the resulting fraction if possible.
For example, let’s subtract 1/2 from 2/3:
Step 1: Find the common denominator, which is 6.
Step 2: Convert 2/3 to an equivalent fraction with a denominator of 6: (2/3) × (2/2) = 4/6.
Step 3: Subtract the numerators: 4/6 – 1/2 = 4/6 – 3/6 = 1/6.
The difference between 2/3 and 1/2 is 1/6.
Multiplication of Rational Numbers
To multiply rational numbers, we can follow these steps:
- Multiply the numerators of both fractions.
- Multiply the denominators of both fractions.
- Simplify the resulting fraction if possible.
For example, let’s multiply 3/5 and 2/7:
Step 1: Multiply the numerators: 3 × 2 = 6.
Step 2: Multiply the denominators: 5 × 7 = 35.
Step 3: The product is 6/35.
The product of 3/5 and 2/7 is 6/35.
Division of Rational Numbers
To divide rational numbers, we can use the following steps:
- Multiply the first fraction (dividend) by the reciprocal of the second fraction (divisor).
- Simplify the resulting fraction if possible.
For example, let’s divide 3/5 by 2/7:
Step 1: Multiply the first fraction by the reciprocal of the second fraction: (3/5) × (7/2) = 21/10.
Step 2: Simplify the resulting fraction if possible.
The quotient of 3/5 divided by 2/7 is 21/10.
These arithmetic operations demonstrate the versatility and applicability of rational numbers in mathematical calculations.
Irreducible Fraction
Every rational number can be expressed in a unique way as an irreducible fraction. An irreducible fraction is a fraction where the numerator and denominator have no common factors other than 1. To obtain the irreducible fraction of a given rational number, divide both the numerator and denominator by their greatest common divisor (GCD). This process ensures that the fraction is in its simplest form.
For example, let’s find the irreducible fraction of 24/36:
Step 1: Find the GCD of 24 and 36, which is 12.
Step 2: Divide both the numerator and denominator by 12: (24/12) ÷ (36/12) = 2/3.
The irreducible fraction of 24/36 is 2/3.
Embedding of Integers
Integers can be embedded within the set of rational numbers. Any integer n can be expressed as the rational number n/1. This embedding allows us to connect the concept of integers with rational numbers, providing a seamless transition between the two number systems.
For example, the integer 5 can be represented as the rational number 5/1.
Equality
Two fractions are equal if and only if their numerators and denominators are equal. In other words, if two fractions are in canonical form, they are equal if and only if their numerators are equal and their denominators are equal.
For example, if we have the fractions 3/4 and 6/8:
3/4 = 6/8 if and only if 3 = 6 and 4 = 8.
In this case, the two fractions are not equal since 3 does not equal 6.
Ordering
Rational numbers can be ordered based on their values. If both denominators are positive, the order can be determined by comparing the numerators. If the numerators are equal, the fraction with the smaller denominator is considered smaller.
For example, if we have the fractions 2/3 and 3/4:
- 2/3 < 3/4 since 2 × 4 = 8 < 3 × 3 = 9.
On the other hand, if either denominator is negative, we must first convert the fractions to an equivalent form with a positive denominator by changing the signs of both the numerator and denominator. Then, we can compare the fractions as mentioned earlier.
Properties of Rational Numbers
Rational numbers possess several important properties that make them a fundamental concept in mathematics. Let’s explore some of these properties:
Closure Property
Rational numbers exhibit closure under addition and multiplication. This means that the sum or product of any two rational numbers is always a rational number.
For example, if we add or multiply two rational numbers, the result will always be a rational number.
Commutative Property
Rational numbers follow the commutative property for addition and multiplication. This property states that the order of the numbers does not affect the result.
For example, for any rational numbers a and b:
- Addition: a + b = b + a
- Multiplication: a × b = b × a
Associative Property
Rational numbers also adhere to the associative property for addition and multiplication. This property states that the grouping of numbers does not affect the result.
For example, for any rational numbers a, b, and c:
- Addition: (a + b) + c = a + (b + c)
- Multiplication: (a × b) × c = a × (b × c)
Identity Property
Rational numbers possess an identity element for both addition and multiplication. The identity element for addition is 0, as adding 0 to any rational number results in the same rational number. The identity element for multiplication is 1, as multiplying any rational number by 1 results in the same rational number.
For example, for any rational number a:
- Addition: a + 0 = a
- Multiplication: a × 1 = a
Inverse Property
Every non-zero rational number has an additive inverse, which is the rational number that, when added to the original number, yields 0. Additionally, every non-zero rational number has a multiplicative inverse, which is the rational number that, when multiplied by the original number, yields 1.
For example, for any non-zero rational number a:
- Additive Inverse: a + (-a) = 0
- Multiplicative Inverse: a × (1/a) = 1
These properties highlight the fundamental nature of rational numbers and their behavior under addition and multiplication.
Continued Fraction Representation
Another way to represent rational numbers is through continued fractions. A finite continued fraction is an expression of the form:
a0 + 1/(a1 + 1/(a2 + 1/(a3 + …))))
where a0, a1, a2, … are integers. Every rational number can be represented as a finite continued fraction, with the coefficients ai determined by applying the Euclidean algorithm to the numerator and denominator of the rational number.
This representation provides an alternative way to express rational numbers and can be useful in certain mathematical calculations and analyses.
The properties and operations discussed above showcase the versatility and significance of rational numbers in the realm of mathematics. They provide a foundation for various mathematical concepts and calculations, enabling us to solve complex problems and explore the intricacies of numbers.
Types of Rational Numbers
Rational numbers encompass a wide range of numbers, each with its own unique characteristics. Let’s explore the different types of rational numbers:
Integers
Integers are a subset of rational numbers. They include positive numbers, negative numbers, and zero. Examples of integers include -3, 0, and 5. Since integers can be expressed as fractions with a denominator of 1, they are considered rational numbers.
Fractions Made up of Integers
Fractions made up of integers are also considered rational numbers. These fractions consist of an integer as the numerator and another integer as the denominator. For example, 3/7 and -2/5 are fractions made up of integers and are therefore rational numbers.
Terminating Decimal Numbers
Terminating decimal numbers are rational numbers that have a finite number of digits after the decimal point. These decimals can be expressed as fractions with a denominator that is a power of 10. For example, 0.25, 0.5, and 0.75 are all terminating decimal numbers and are therefore rational numbers.
Non-terminating Decimal Numbers With Infinitely Repeating Patterns
Non-terminating decimal numbers with infinitely repeating patterns are also rational numbers. These decimals have a repetitive sequence of digits that continues indefinitely. They can be expressed as fractions with a denominator that corresponds to the repeating pattern. For example, 0.333…, 0.141414…, and 0.619619… are non-terminating decimal numbers with infinitely repeating patterns and are therefore rational numbers.
Positive Rational Numbers
Positive rational numbers are rational numbers that are greater than zero. They include positive integers, positive fractions, and positive terminating and non-terminating decimals. Examples of positive rational numbers include 1/2, 3/4, and 0.625.
Negative Rational Numbers
Negative rational numbers are rational numbers that are less than zero. They include negative integers, negative fractions, and negative terminating and non-terminating decimals. Examples of negative rational numbers include -1/3, -2/5, and -0.75.
These different types of rational numbers showcase the versatility and diversity within the realm of rational numbers.
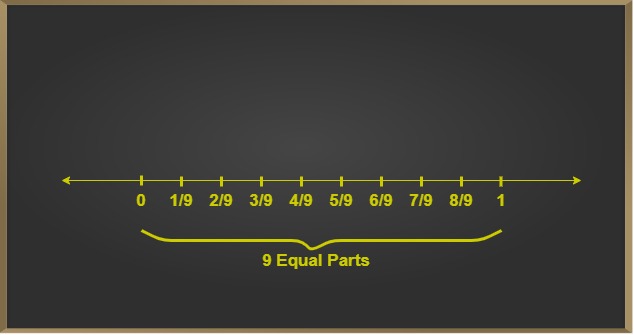
Representing Rational Numbers on a Real Line
Rational numbers can be represented on a real number line, providing a visual representation of their magnitude and position. The real number line extends infinitely in both positive and negative directions, with zero at its center.
To represent rational numbers on a real line, we can assign each rational number a specific position based on its value. For example, the rational number 1/2 would be represented halfway between 0 and 1 on the positive side of the number line. Similarly, the rational number -3/4 would be positioned three-fourths of the way between 0 and -1 on the negative side of the number line.
This visual representation helps us understand the relative positions and magnitudes of different rational numbers, allowing for better comprehension and analysis.
Solved Examples on Rational Numbers
To solidify our understanding of rational numbers, let’s explore some solved examples:
Example 1: Adding Rational Numbers
- Problem: Add 2/3 and 1/4.
- Solution: To add these fractions, we first find a common denominator. In this case, the common denominator is 12. Converting the fractions to equivalent fractions with a denominator of 12, we get 8/12 and 3/12. Adding the numerators, we have 8/12 + 3/12 = 11/12. Therefore, the sum of 2/3 and 1/4 is 11/12.
Example 2: Subtracting Rational Numbers
- Problem: Subtract 3/5 from 4/7.
- Solution: To subtract these fractions, we first find a common denominator. In this case, the common denominator is 35. Converting the fractions to equivalent fractions with a denominator of 35, we get 20/35 and 15/35. Subtracting the numerators, we have 20/35 – 15/35 = 5/35. Simplifying the resulting fraction, we get 1/7. Therefore, the difference between 4/7 and 3/5 is 1/7.
Example 3: Multiplying Rational Numbers
- Problem: Multiply 2/3 by 5/8.
- Solution: To multiply these fractions, we simply multiply the numerators and denominators separately. Multiplying 2/3 by 5/8, we have (2 × 5)/(3 × 8) = 10/24. Simplifying the resulting fraction, we get 5/12. Therefore, the product of 2/3 and 5/8 is 5/12.
Example 4: Dividing Rational Numbers
- Problem: Divide 3/4 by 2/5.
- Solution: To divide these fractions, we multiply the first fraction by the reciprocal of the second fraction. In this case, we have (3/4) ÷ (2/5) = (3/4) × (5/2) = 15/8. Simplifying the resulting fraction, we get 15/8. Therefore, the quotient of 3/4 divided by 2/5 is 15/8.
These examples highlight the application of rational numbers in various mathematical operations, enabling us to solve problems and perform calculations accurately.
How Kunduz Can Help You Learn Rational Numbers?
Understanding rational numbers and their various properties and operations can be challenging at times. However, with the help of Kunduz, you can enhance your learning experience and master the concepts related to rational numbers.
Kunduz offers a comprehensive range of educational resources, including interactive lessons, practice exercises, and personalized feedback. With Kunduz, you can access step-by-step explanations, examples, and solved problems, allowing you to strengthen your understanding of rational numbers. Whether you need assistance with addition, subtraction, multiplication, division, or any other topic related to rational numbers, Kunduz is here to support you every step of the way.
By leveraging Kunduz’s user-friendly platform and extensive educational materials, you can confidently navigate the world of rational numbers and excel in your mathematical journey. Empower yourself with the knowledge and skills necessary to solve complex problems and unlock your full potential in mathematics.
