In the world of geometry, a rectangular prism is a fascinating three-dimensional shape that has various applications in both mathematics and everyday life. Also known as a cuboid, a rectangular prism is defined by its six faces, which are all rectangles, and its unique set of properties. This article will explore the definition, types, properties, formulas, and examples of rectangular prisms, providing a comprehensive understanding of this geometric shape.
What is the Rectangular Prism?
A rectangular prism is a solid shape that is bounded by six faces, with the two faces being the bases (top and bottom) and the other four faces being the lateral faces. Each face of the prism is in the shape of a rectangle, and the opposite faces are congruent or identical. This means that if you were to measure the length and width of one face, you would find that it matches the length and width of the opposite face.
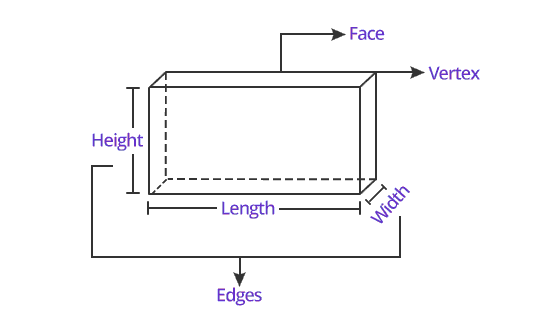
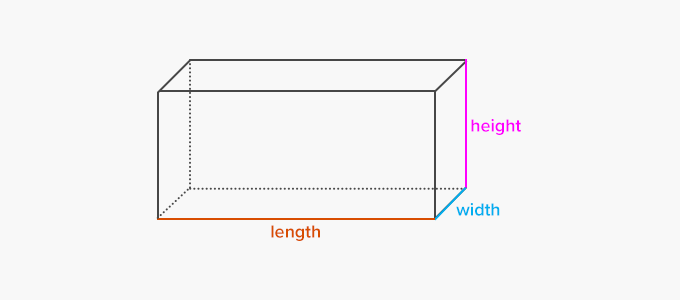
The rectangular prism has three dimensions: length, width, and height. These dimensions determine the size and proportions of the prism. Real-life examples of rectangular prisms include shoe boxes, books, storage containers, and rooms within a building.
Types of Rectangular Prisms
Rectangular prisms can be classified into two types based on the angles formed by their lateral faces with the bases: right rectangular prisms and oblique rectangular prisms.
Right Rectangular Prism
A right rectangular prism is a type of rectangular prism where all the faces are perpendicular to the bases. In other words, the lateral faces form right angles with the bases. This type of prism is often referred to as a cuboid. Examples of cuboids include rectangular tissue boxes, bricks, and notebooks.

Oblique Rectangular Prism
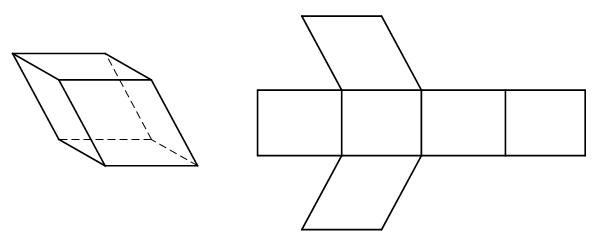
An oblique rectangular prism, on the other hand, is a rectangular prism where the lateral faces are not perpendicular to the bases. Instead, the lateral faces are parallelograms. Unlike the right rectangular prism, the oblique rectangular prism does not have all right angles. While less common, oblique rectangular prisms can still be found in various objects, such as tilted storage containers or slanted roofs.
Properties of Rectangular Prism
Rectangular prisms possess several unique properties that make them distinct from other three-dimensional shapes. Understanding these properties can provide insights into their characteristics and behavior. Here are some key properties of rectangular prisms:
- Faces: A rectangular prism has six faces in total. These faces include the top and bottom bases and the four lateral faces.
- Edges: A rectangular prism has twelve edges or sides. Each edge is formed by the intersection of two faces.
- Vertices: A rectangular prism has eight vertices or corners. Each vertex is formed by the intersection of three edges.
- Right Angles: In a right rectangular prism, all the angles formed between the edges and faces are right angles (90 degrees). This property is not applicable to oblique rectangular prisms.
- Identical Opposite Faces: The opposite faces of a rectangular prism are congruent or identical. This means that if you were to measure the length and width of one face, it would be the same as the length and width of the opposite face.
- Rectangular Cross-Section: A rectangular prism has a rectangular cross-section along its length. This means that if you were to cut the prism perpendicular to its length, the resulting shape would be a rectangle.
These properties define the fundamental characteristics of a rectangular prism and distinguish it from other geometric shapes.
Rectangular Prism Formulas
Formulas are essential tools for calculating various measurements and properties of rectangular prisms. Whether you need to find the volume, surface area, or diagonal length of a rectangular prism, these formulas provide the necessary mathematical relationships. Let’s explore the formulas commonly used for rectangular prisms:
Volume of a Rectangular Prism Formula
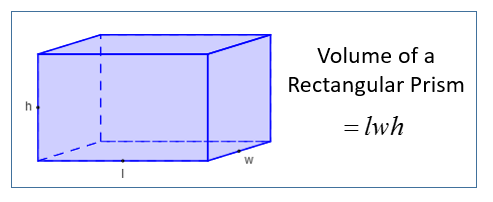
The volume of a rectangular prism represents the amount of space it occupies. It is calculated by multiplying the length (l), width (w), and height (h) of the prism. The formula for finding the volume of a rectangular prism is:
Volume (V) = length × width × height
This formula can be easily applied to find the volume of any rectangular prism by substituting the appropriate values for length, width, and height.
Surface Area of a Rectangular Prism
The surface area of a rectangular prism refers to the total area covered by its faces. It is essential to calculate the surface area when determining the amount of material needed to cover the prism or when analyzing its external characteristics. The surface area consists of two components: the lateral surface area and the total surface area.
Lateral Surface Area
The lateral surface area (LSA) of a rectangular prism is the sum of the areas of all its lateral faces, excluding the bases. To calculate the LSA, you can use the formula:
Lateral Surface Area (LSA) = 2 × (width × height + length × height)
This formula considers the dimensions of the width, length, and height to determine the lateral surface area. It provides a measure of the total area covered by the sides of the prism.
Total Surface Area
The total surface area (TSA) of a rectangular prism is the sum of the areas of all its faces, including the bases. To calculate the TSA, you can use the formula:
Total Surface Area (TSA) = 2 × (length × width + width × height + length × height)
This formula takes into account the dimensions of the length, width, and height to determine the total surface area of the prism. It provides a measure of the total area covered by all the faces, including the bases.
These formulas enable precise calculations of the volume and surface area of rectangular prisms, allowing for accurate measurements and analysis.
Space Diagonal of Rectangular Prism
The space diagonal of a rectangular prism refers to the length of the line segment connecting two non-adjacent vertices. It provides valuable information about the diagonal distance within the prism. To calculate the space diagonal (D) of a rectangular prism, you can use the formula:
Diagonal (D) = √(length² + width² + height²)
This formula utilizes the Pythagorean theorem to determine the length of the space diagonal. It considers the dimensions of the length, width, and height to provide the diagonal length of the prism.
Rectangular Prism Shape
The shape of a rectangular prism is defined by its six faces, which are all rectangles. These faces contribute to the overall appearance and characteristics of the prism. The top and bottom faces, known as the bases, are congruent rectangles, while the four lateral faces are rectangular in shape. The opposite faces are identical, meaning that if you were to measure the length and width of one face, it would be the same as the length and width of the opposite face.
The rectangular cross-section along the length of the prism further accentuates its shape. When viewed from different angles, the rectangular prism may appear elongated or compact, depending on the relative proportions of its length, width, and height. The shape of a rectangular prism allows for efficient stacking and packing, making it ideal for various applications in construction, storage, and manufacturing.
Rectangular Prism Net
A rectangular prism net is a two-dimensional representation of the prism when its faces are unfolded or opened on a flat plane. It shows the layout and dimensions of each face, allowing for a visual understanding of how the prism is constructed. By examining the net of a rectangular prism, you can determine the individual areas of each face and calculate the total surface area.
The net of a rectangular prism consists of six rectangles, representing the six faces of the prism. Each rectangle corresponds to a specific face and has dimensions equivalent to the corresponding face’s length and width. By applying the formula for the area of a rectangle, you can find the areas of the individual faces and sum them to obtain the total surface area of the prism.
The net of a rectangular prism is a valuable tool for understanding the geometry and characteristics of the shape. It provides a clear representation of the arrangement and dimensions of the prism’s faces, aiding in calculations and visualizations.

Solved Examples On Rectangular Prism
To solidify our understanding of rectangular prisms, let’s solve a few examples that involve finding the volume, surface area, and other measurements. These examples will demonstrate the practical application of the formulas and concepts discussed earlier.
Example 1: Finding the Volume of a Rectangular Prism
Question: Find the volume of a rectangular prism whose length, width, and height are 8 cm, 6 cm, and 4 cm, respectively.
Solution: Given: Length (l) = 8 cm Width (w) = 6 cm Height (h) = 4 cm
The formula for finding the volume of a rectangular prism is: Volume (V) = length × width × height
Substituting the given values into the formula: Volume (V) = 8 cm × 6 cm × 4 cm = 192 cm³
Therefore, the volume of the rectangular prism is 192 cm³.
Example 2: Finding the Surface Area of a Rectangular Prism
Question: Find the surface area of a rectangular prism whose length, width, and height are 8 cm, 6 cm, and 4 cm, respectively.
Solution: Given: Length (l) = 8 cm Width (w) = 6 cm Height (h) = 4 cm
The formula for finding the surface area of a rectangular prism is: Total Surface Area (TSA) = 2 × (length × width + width × height + length × height)
Substituting the given values into the formula: TSA = 2 × (8 cm × 6 cm + 6 cm × 4 cm + 8 cm × 4 cm) = 208 cm²
Therefore, the surface area of the rectangular prism is 208 cm².
These solved examples demonstrate how to apply the formulas for volume and surface area to find the measurements of rectangular prisms accurately.
How Many Edges and Vertices does a Rectangular Prism Have?
Understanding the number of edges and vertices in a rectangular prism is crucial for comprehending its overall structure. Let’s explore the number of edges and vertices a rectangular prism possesses.
A rectangular prism has 12 edges in total. Each edge is formed by the intersection of two faces of the prism.
Additionally, a rectangular prism has 8 vertices or corners. Each vertex is formed by the intersection of three edges.
These edges and vertices contribute to the distinct characteristics of rectangular prisms and are essential for their identification and analysis.
Conclusion
Rectangular prisms, also known as cuboids, are fascinating three-dimensional shapes with a wide range of applications in mathematics and everyday life. Defined by their six rectangular faces and unique properties, rectangular prisms offer a wealth of opportunities for exploration and understanding. By utilizing the formulas for volume, surface area, and diagonal length, we can accurately measure and analyze these prisms. The shape and net of a rectangular prism further enhance our comprehension of its structure and characteristics. By solving examples and understanding the number of edges and vertices, we solidify our knowledge of rectangular prisms and their properties. Embrace the world of rectangular prisms, and unlock the secrets of this versatile geometric shape.
For those fascinated by three-dimensional geometry, our tetrahedron page offers a captivating exploration into the unique properties of tetrahedra, providing a distinct perspective that complements the study of various polyhedral shapes.
