When working with angles in mathematics and trigonometry, understanding reference angles is crucial. Reference angles are a key concept that helps us simplify calculations and solve problems involving angles. In this article, we will explore what reference angles are, how to find them, and their applications in various contexts.
What is the Reference Angle?
A reference angle is the smallest acute angle formed between the terminal side of an angle and the x-axis on a coordinate plane. It is always positive and falls within the range of 0 to 90 degrees or 0 to π/2 radians. The reference angle provides a reference point for understanding and computing trigonometric functions of any given angle.
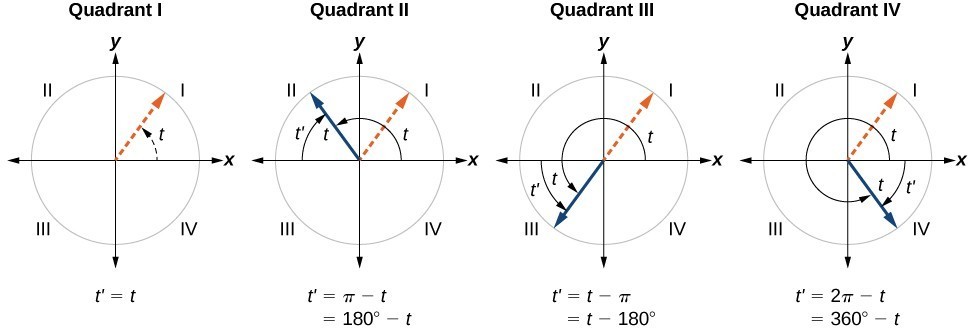
How to Draw Reference Angle?
To draw the reference angle for a given angle, we need to identify the terminal side of the angle and determine the angle formed between the terminal side and the x-axis. This angle is the reference angle. By visualizing the position of the terminal side in relation to the x-axis, we can determine the reference angle accurately.
Rules for Reference Angles in Each Quadrant
The reference angle formulas vary depending on the quadrant in which the given angle lies. Here are the reference angle formulas for each quadrant:
| Quadrant | Angle (θ) | Reference Angle Formula in Degrees | Reference Angle Formula in Radians |
|---|---|---|---|
| I | 0° to 90° | θ | θ |
| II | 90° to 180° | 180° – θ | π – θ |
| III | 180° to 270° | θ – 180° | θ – π |
| IV | 270° to 360° | 360° – θ | 2π – θ |
If the angle is measured in radians, the same rules apply, but the measurements are made in terms of π. For example, 180° is equivalent to π radians, and 360° is equivalent to 2π radians.
Reference Angle Formula
The reference angle formula provides a straightforward way to calculate the reference angle for any given angle. The formula depends on the quadrant in which the angle falls. By applying the appropriate formula, we can easily find the reference angle.
How to Find Reference Angles?
To find the reference angle for a given angle, follow these steps:
Step 1: Determine the quadrant in which the angle lies.
Step 2: Apply the corresponding reference angle formula based on the quadrant.
Step 3: Calculate the reference angle using the formula.
Step 4: The calculated reference angle is the answer.
Let’s go through an example to illustrate the process.
Example: Find the reference angle of 120°.
Solution:
Step 1: The angle 120° lies in quadrant II.
Step 2: Using the reference angle formula for quadrant II (180° – θ), we have: Reference Angle = 180° – 120° = 60°
Therefore, the reference angle of 120° is 60°.
Unit Circle Reference Angle
The unit circle is a powerful tool in trigonometry that helps us understand the relationship between angles, coordinates, and trigonometric functions. When working with reference angles, the unit circle becomes particularly useful. By examining the coordinates of points on the unit circle, we can determine the reference angles for various angles.
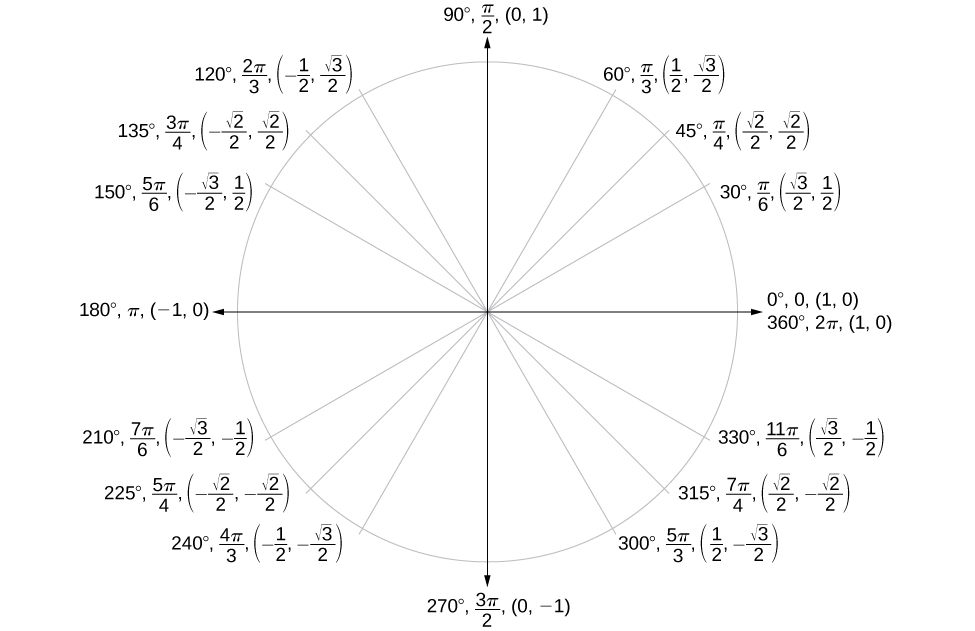
Types of Reference Angle
While all reference angles serve the same purpose of simplifying calculations, there are different types of reference angles, such as normal reference angles, parallel reference angles, and perpendicular reference angles. Each type has its own unique properties and applications in different contexts.
Reference Angles and Trigonometric Functions
Reference angles play a significant role in evaluating trigonometric functions for angles beyond 90 degrees. By using reference angles, we can find the values of trigonometric functions at specific angles and simplify complex calculations. The relationship between reference angles and trigonometric functions allows us to work with angles in a more manageable and efficient manner.
Properties of Reference Angle
Reference angles possess certain properties that are useful in various mathematical applications. Some important properties of reference angles include:
- Reference angles are always positive.
- The reference angle of an angle is always smaller than or equal to 90 degrees.
- The reference angle of a positive angle is the same as the angle itself.
- The reference angle of a negative angle is the same as the reference angle of its positive counterpart.
Solved Examples on Reference Angle
To deepen our understanding of reference angles, let’s work through a few solved examples:
Example 1: Find the reference angle of -45°.
Solution: Step 1: The angle -45° lies in quadrant IV. Step 2: Using the reference angle formula for quadrant IV (360° – θ), we have: Reference Angle = 360° – (-45°) = 405°
Therefore, the reference angle of -45° is 405°.
Example 2: Find the reference angle of 5π/4 radians.
Solution: Step 1: The angle 5π/4 radians lies in quadrant III. Step 2: Using the reference angle formula for quadrant III (θ – π), we have: Reference Angle = 5π/4 – π = π/4 radians
Therefore, the reference angle of 5π/4 radians is π/4 radians.
Example 3: Find the reference angle of 140°.
Solution: The given angle is, θ = 140°. We know that 140° lies in quadrant II. Using the above rules, its reference angle is 180 – θ = 180 – 140 = 40°. Therefore, the reference angle of 140° is 40°.
How Kunduz Can Help You Learn Reference Angles?
Kunduz is a comprehensive learning platform that provides various resources and tools to help you master reference angles and other mathematical concepts. Whether you are a student, educator, or simply someone interested in expanding your mathematical knowledge, Kunduz is here to support your learning journey.
