In geometry and mathematics, understanding the concept of slope is crucial for analyzing and interpreting the characteristics of lines on a coordinate plane. The rise over run, also known as the slope, is a fundamental concept that helps determine the steepness and direction of a line. By calculating the rise and run between two points on a line, we can find the slope and gain valuable insights into the line’s behavior.
What is the Rise Over Run?
The rise over run is a mathematical concept used to calculate the slope of a line. It refers to the ratio of the change in the y-coordinate (vertical change) to the change in the x-coordinate (horizontal change) between two points on a line. The rise is the difference between the y-coordinates of the two points, while the run is the difference between the x-coordinates.
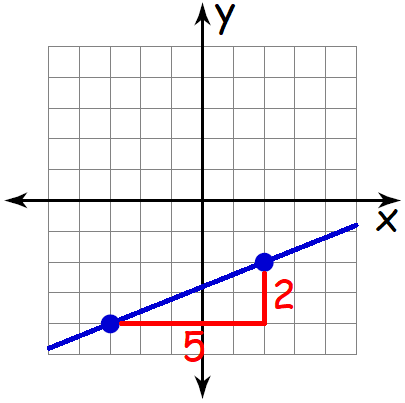
What is Slope?
Slope is a measure of the steepness and direction of a line. It quantifies the rate at which the line rises or falls as it moves horizontally. The slope can be positive, negative, zero, or undefined, depending on the characteristics of the line.
What is the Slope of a Line?
The slope of a line is a measure of its inclination and is determined by the rise over run formula. It represents the change in the y-coordinate per unit change in the x-coordinate. The slope can be calculated by dividing the rise by the run, yielding a numeric value that describes the line’s steepness and direction.

Rise Over Run Formula
The rise over run formula (or slope formula) calculates the slope of a line between two points, A(x1, y1) and B(x2, y2). It can be expressed as:
Slope (m) = (y2 – y1) / (x2 – x1)
This formula represents the ratio of the vertical change (rise) to the horizontal change (run) between the two points on the line. By substituting the coordinates of the two points into the formula, we can easily calculate the slope.
How To Find Rise Over Run
To find the rise over run (slope) between two points, follow these steps:
Step 1: Identify the coordinates of the two points on the line.
Step 2: Determine the difference in the y-coordinates (rise) and the difference in the x-coordinates (run) between the two points.
Step 3: Substitute the values into the rise over run formula: Slope (m) = (y2 – y1) / (x2 – x1)
Step 4: Simplify the expression to obtain the slope value.
Rules of Rise Over Run Formula
The rise over run formula follows certain rules that govern its behavior:
- Positive Slope: If the line rises from left to right, the slope is positive. The rise over run ratio will be positive, indicating an upward trend.
- Negative Slope: If the line falls from left to right, the slope is negative. The rise over run ratio will be negative, indicating a downward trend.
- Zero Slope: If the line is horizontal, the slope is zero. The rise over run ratio will be zero, indicating no change in the y-coordinate for every unit change in the x-coordinate.
- Undefined Slope: If the line is vertical, the slope is undefined. The rise over run ratio involves division by zero, which is undefined.
Rise-Over-Run Ratio Calculation
The rise over run ratio is an essential metric for understanding the characteristics of a line. It helps determine the line’s steepness and direction, as well as its relationship to other lines and coordinate axes.
To calculate the rise over run ratio, follow these steps:
Step 1: Identify two points on the line with coordinates (x1, y1) and (x2, y2).
Step 2: Determine the difference in the y-coordinates (rise) by subtracting y1 from y2.
Step 3: Determine the difference in the x-coordinates (run) by subtracting x1 from x2.
Step 4: Divide the rise by the run to obtain the rise over run ratio.
The rise over run ratio is expressed as a fraction, representing the change in the y-coordinate per unit change in the x-coordinate.
Applications Of Rise Over Run
The rise over run formula and the concept of slope have numerous applications in various fields, including:
- Coordinate Geometry: The slope of a line helps determine the relationship between two lines, such as parallelism, perpendicularity, and collinearity. It also helps define the placement of a line with respect to the coordinate axes.
- Equations of Lines: The slope is a crucial component in determining the equation of a line. It is used in various forms, such as point-slope form and slope-intercept form, to write the equation of a line.
- Angle between Lines: The slope can be used to find the angle between two lines. By comparing the slopes, we can calculate the angle using trigonometric functions.
- Graphical Analysis: The slope provides insights into the behavior of functions and relationships between variables. It helps analyze trends, rates of change, and the direction of relationships in graphical representations.
- Real–World Applications: The concept of slope is widely used in fields such as physics, engineering, economics, and architecture to model and analyze various phenomena.
How to Use Rise Over Run to Find Slope?
To use the rise over run formula to find the slope of a line, follow these steps:
Step 1: Identify two points on the line with coordinates (x1, y1) and (x2, y2).
Step 2: Determine the difference in the y-coordinates (rise) by subtracting y1 from y2.
Step 3: Determine the difference in the x-coordinates (run) by subtracting x1 from x2.
Step 4: Divide the rise by the run to obtain the slope.
By following these steps, you can easily calculate the slope of a line using the rise over run formula.
How do you convert rise and run to an angle?
To convert the rise and run of a line to an angle, you can use trigonometric functions such as tangent. The tangent of an angle is equal to the rise over run ratio. By taking the inverse tangent (arctan) of the rise over run ratio, you can find the angle between the line and the x-axis.
How do you find rise and run on a graph?
To find the rise and run on a graph, you need to identify two points on the line. Then, determine the difference in the y-coordinates (rise) by subtracting the y-coordinate of the first point from the y-coordinate of the second point. Similarly, determine the difference in the x-coordinates (run) by subtracting the x-coordinate of the first point from the x-coordinate of the second point.
By following these steps, you can find the rise and run on a graph and use them to calculate the slope of the line.
Solved Examples on Rise Over Run
Example 1: Find the slope of the line passing through the points (2, 4) and (6, 10).
Solution:
Step 1: Identify the coordinates of the two points: (2, 4) and (6, 10).
Step 2: Determine the rise: 10 – 4 = 6.
Step 3: Determine the run: 6 – 2 = 4.
Step 4: Divide the rise by the run: 6/4 = 3/2. Therefore, the slope of the line is 3/2.
Example 2: Determine the slope of the line passing through the points (-3, 5) and (1, 1).
Solution:
Step 1: Identify the coordinates of the two points: (-3, 5) and (1, 1).
Step 2: Determine the rise: 1 – 5 = -4.
Step 3: Determine the run: 1 – (-3) = 4.
Step 4: Divide the rise by the run: -4/4 = -1. Therefore, the slope of the line is -1.
Example 3: Find the slope of the line with the equation y = 2x + 3.
Solution: The given equation is in slope-intercept form, y = mx + b, where m represents the slope. Comparing the equation with the slope-intercept form, we can see that the slope is 2. Therefore, the slope of the line is 2.
How Kunduz Can Help You Learn Rise Over Run?
Kunduz is your ultimate companion for learning rise over run and other mathematical concepts. With our comprehensive and interactive resources, you can grasp the fundamentals of slope, understand the rise over run formula, and apply it to various real-world applications. Our expert instructors provide step-by-step guidance, solved examples, and practice questions to ensure your mastery of the topic. Whether you’re a student, teacher, or enthusiast, Kunduz is here to support your learning journey and help you achieve academic success.
