Welcome to an in-depth exploration of scale factor in mathematics! In this article, we will delve into the definition, formula, derivation, examples, and facts about scale factor. Whether you’re a student learning about geometry or a curious individual interested in understanding the concept of scale, this article will provide you with all the essential information you need.
An Introduction to Scale Factor
In the field of mathematics, scale factor is a fundamental concept that allows us to change the size of a figure while maintaining its shape. It is a ratio that compares the measurements of a given object to the measurements of its representation, which can be either larger or smaller. By using the scale factor, we can create similar figures with different dimensions.
What is Scale?
Before we dive deeper into scale factor, let’s take a moment to understand the concept of scale itself. In the realm of mathematics and geometry, scale refers to the ratio between the measurements of an object and its representation. It allows us to create accurate reproductions of figures, ensuring that they are different in size but maintain the same proportions.

What is the Scale Factor?
The scale factor is the numerical value that represents the ratio between the measurements of an object and its representation. It defines how much larger or smaller the representation is in comparison to the original object. The scale factor can be expressed as a fraction, a decimal, or a ratio.
When the scale factor is a whole number, the representation is larger than the original object. For example, a scale factor of 2 means that the representation is twice the size of the original object. Conversely, when the scale factor is a fraction, the representation is smaller than the original object. For instance, a scale factor of 1/2 indicates that the representation is half the size of the original object.
Scale Factor Formula
To calculate the scale factor, we use a simple formula:
Scale Factor = Dimension of New Shape / Dimension of Original Shape
This formula allows us to determine the scale factor by comparing the dimensions of the new shape to the dimensions of the original shape. By dividing these measurements, we can find the numerical value of the scale factor.
How to Find the Scale Factor?
Finding the scale factor involves determining whether we are scaling up or scaling down and then comparing the corresponding measurements of the new and original shapes.
Scale Up
When scaling up, we are increasing the size of the original shape. To find the scale factor for scaling up, we divide the larger measurement by the smaller measurement. This ratio will be greater than 1.
Scale Down
When scaling down, we are reducing the size of the original shape. To find the scale factor for scaling down, we divide the smaller measurement by the larger measurement. This ratio will be less than 1.
How to Find the Scale factor of Enlargement
To find the scale factor of an enlargement, we simply multiply the dimensions of the original shape by the scale factor. This will give us the dimensions of the new, enlarged shape.
For example, let’s say we have a rectangle with a length of 4 cm and a width of 2 cm. If we want to increase the size of this rectangle by a scale factor of 4, we would multiply each dimension by 4. The new dimensions would be a length of 16 cm and a width of 8 cm.
How to Make a Scale Model?
A scale model is a representation of an object that is accurate to a specific scale factor. It allows us to visualize and understand large or complex objects in a smaller, more manageable form. To create a scale model, we need accurate plans or drawings of the original object, which are typically created using a scale factor to reduce the dimensions of the object.
To make a scale model, we multiply every measurement on the original drawing by the scale factor to determine the correct sizes for the model parts. For example, if we are building a model of a 32-foot long shed using a scale factor of 1:87, the length of the model shed would be 4.4 inches.
How to Use Scale Factor?
Scale factor is a versatile tool that finds applications in various fields. Here are some common ways to use scale factor:
- Drawing Similar Figures: In geometry, scale factor is used to draw similar figures. By multiplying the dimensions of the original figure by the scale factor, we can create a proportionate representation of the figure with different dimensions.
- Creating Scale Models: Scale factor is essential in creating accurate scale models of objects. By using the appropriate scale factor, we can shrink large objects to a manageable size while maintaining their proportions.
- Blueprints and Architecture: Scale factor is used in creating blueprints and scale plans for machinery and architecture. It allows designers and architects to work with models of objects that are too large to physically handle at their actual size.
- Maps: Scale factor is crucial in creating maps. It enables us to represent vast lands and regions on a small piece of paper, making it easier to navigate and understand geographical features.
- Proportional Relationships: Scale factor is used to establish proportional relationships between different quantities. It allows us to compare and analyze ratios and proportions in various contexts.
Scale Factor Problem
Let’s explore a problem to apply the concept of scale factor. Suppose we have a rectangle with dimensions of 6 cm and 3 cm. We want to increase the scale factor of this rectangle by 2 and 3, respectively. This means we want to enlarge the rectangle by multiplying each dimension by the corresponding scale factor.
By multiplying the original dimensions by 2, we get a new rectangle with dimensions of 12 cm and 6 cm. Similarly, by multiplying the original dimensions by 3, we obtain a new rectangle with dimensions of 18 cm and 9 cm.
Scale Factor of Triangle
The scale factor can also be applied to triangles. When dealing with similar triangles, which have the same shape but different sizes, the scale factor represents the ratio of corresponding sides.
For example, let’s consider two similar triangles. If the legs of the smaller triangle measure 12 cm, and the legs of the larger triangle measure 36 cm, we can determine the scale factor by dividing the larger measurement by the smaller measurement. In this case, the scale factor is 3, indicating that the larger triangle is three times the size of the smaller triangle.
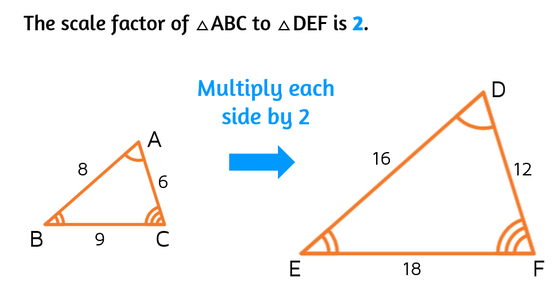
How Does the Scale Factor Work?
The scale factor determines the relationship between the original shape and its representation. When the scale factor is greater than 1, the representation is larger than the original shape. Conversely, when the scale factor is less than 1, the representation is smaller. A scale factor of 1 indicates that the representation is the same size as the original shape.
By using reciprocal scale factors, we can reverse the scaling process. For example, if we scale a shape using a scale factor of 4 to create a larger representation, we can scale the larger representation back to the original size using a reciprocal scale factor of 1/4.
Scale on a Graph
Scale is an important concept in graphing. It allows us to measure and quantify objects on a graph. A scale on a graph consists of a set of numbers that help us measure or quantify objects. The scale shows how numbers or pictures are used in data representation.
For example, in a bar graph, the vertical axis represents the quantity being measured, while the horizontal axis represents the categories or variables being compared. The numbers on the vertical axis are marked at equal intervals, indicating the scale used for the graph.

The Size of the Scale Factor
The size of the scale factor determines the magnitude of the enlargement or reduction of a shape. When the scale factor is greater than 1, the representation is larger than the original shape. As the scale factor increases, the size of the representation becomes more significantly larger. Conversely, when the scale factor is less than 1, the representation is smaller than the original shape. The smaller the scale factor, the more significantly the representation is reduced in size.
Solved Examples on Scale Factor
Let’s explore some solved examples to further understand the concept of scale factor.
Example 1: Find the scale factor when a square of side length 4 cm is enlarged to make a square of side length 8 cm.
Solution: To find the scale factor, we divide the side length of the larger square by the side length of the smaller square.
Scale Factor = 8 cm / 4 cm = 2
Hence, the scale factor from the larger square to the smaller square is 2.
Example 2: A triangle with side lengths of 3 cm, 4 cm, and 5 cm has been enlarged by a scale factor of 4. What are the dimensions of the new triangle?
Solution: To find the dimensions of the new triangle, we multiply each side length of the original triangle by the scale factor.
New Side Lengths = (3 cm × 4, 4 cm × 4, 5 cm × 4) = (12 cm, 16 cm, 20 cm)
Therefore, the dimensions of the new triangle are 12 cm, 16 cm, and 20 cm.
Frequently Asked Questions on Scale Factor
What Happens if the Scale Factor is Greater Than 1?
When the scale factor is greater than 1, the resulting figure is an enlargement of the original figure.
How to Reduce a Shape by a Scale Factor?
To reduce a shape by a scale factor, you multiply all dimensions of the original shape by the scale factor (which is less than 1).
What Does a Scale Factor of 0.5 Mean?
A scale factor of 0.5 means the new shape will be half the size of the original figure.
What Happens if the Scale Factor is Less Than 1?
When the scale factor is less than 1, the resulting figure is a reduction (smaller version) of the original figure.
What Does a Negative Scale Factor Mean?
A negative scale factor results in a dilated and rotated figure by 180 degrees.
What Scale Factor makes a Figure Smaller?
A scale factor less than 1 produces a smaller figure.
How is a Scale Different from a Scale Factor?
While the scale represents the relationship between an object and its model or representation, the scale factor is the multiplier applied to all dimensions of an object to create a proportional enlargement or reduction of the original shape.
How Kunduz Can Help You Learn Scale Factor?
At Kunduz, we are committed to helping students master mathematical concepts like scale factor. Our experienced tutors provide personalized guidance, clear explanations, and interactive learning materials to ensure a comprehensive understanding of the subject. With our support, you can confidently navigate the world of scale factor and excel in your mathematical journey.
Remember, scale factor plays a crucial role in various fields, including geometry, architecture, and design. By understanding its principles and applications, you can enhance your problem-solving skills and gain a deeper appreciation for the beauty of mathematics. So, embrace the world of scale factor and embark on a rewarding learning journey with Kunduz!
