Triangles are fundamental shapes in geometry, consisting of three sides, three angles, and three vertices. They play a crucial role in various mathematical and real-world applications. Triangles can be classified based on the lengths of their sides and the measures of their angles. One such classification is the scalene triangle.
In this article, we will explore the concept of the scalene triangle, including its definition, properties, and various types. We will also delve into the formulas used to calculate the area and perimeter of a scalene triangle. So let’s dive into the fascinating world of the scalene triangle!
What is the Scalene Triangle?
A scalene triangle is a type of triangle that has three unequal side lengths and three different angle measurements. Unlike equilateral triangles, where all sides are equal, and isosceles triangles, where two sides are equal, scalene triangles have no equal sides. This uniqueness makes scalene triangles intriguing and versatile in various geometric applications.
To visualize a scalene triangle, imagine three sides of different lengths intersecting to form three angles of different measures. Each side of the triangle is labeled with a different symbol or measurement, indicating its inequality with the other sides. Similarly, each angle is labeled with a different measurement, emphasizing their distinctiveness.

Parts of Scalene Triangle
Before we explore the properties and types of scalene triangles, let’s familiarize ourselves with the essential parts of a triangle, including the scalene triangle.
- Sides: The sides of a triangle are the line segments that connect the vertices. In a scalene triangle, all three sides have different lengths, setting it apart from other types of triangles.
- Vertices: The vertices are the points where the sides of a triangle meet. A scalene triangle has three vertices, each representing the endpoint of a side.
- Angles: The angles of a triangle are formed by the intersection of its sides. In a scalene triangle, all three angles have different measures, distinguishing it from other types of triangles.
Types of Scalene Triangles
Scalene triangles can further be categorized into three types based on the measures of their angles: acute-angled scalene triangles, obtuse-angled scalene triangles, and right-angled scalene triangles. Let’s explore each type in more detail:
Acute-angled scalene triangle
An acute-angled scalene triangle is a triangle in which all three angles are less than 90 degrees. In other words, all angles in this type of scalene triangle are acute angles. Acute angles are angles that measure less than 90 degrees. The sum of all three angles in any triangle, including the acute-angled scalene triangle, is always 180 degrees.
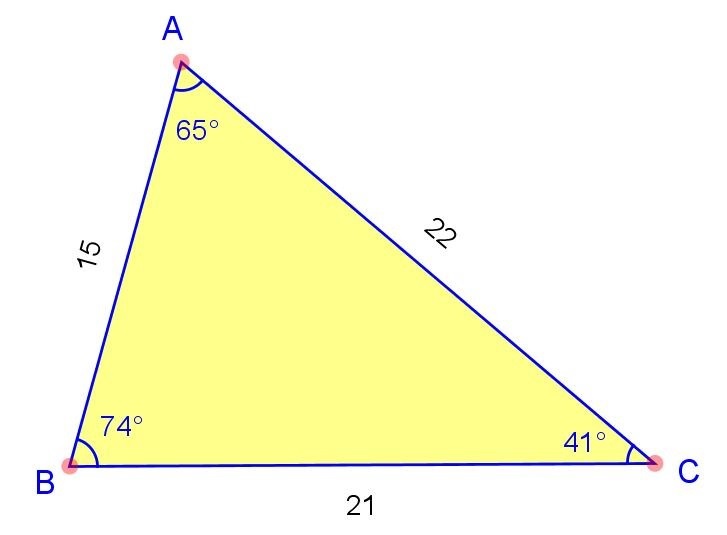
Obtuse-angled scalene triangle
An obtuse-angled scalene triangle is a triangle in which one of the angles is greater than 90 degrees but less than 180 degrees. The other two angles in this type of scalene triangle are acute angles, measuring less than 90 degrees. Similar to all triangles, the sum of the three angles in an obtuse-angled scalene triangle is always 180 degrees.
Right-angled scalene triangle
A right-angled scalene triangle is a triangle that has one right angle, measuring exactly 90 degrees. The other two angles in this type of scalene triangle are acute angles, measuring less than 90 degrees. As with all triangles, the sum of the three angles in a right-angled scalene triangle is always 180 degrees.
It is important to note that in a scalene triangle, the classification is based on the lengths of the sides, not just the measures of the angles. Hence, a scalene triangle can be acute-angled, obtuse-angled, or right-angled, depending on the measures of its angles.
Types of Scalene Triangles, Sides, Angles Table
To summarize the different types of scalene triangles based on their sides and angles, refer to the table below:
| Triangle Type | Sides | Angles |
|---|---|---|
| Acute-angled scalene triangle | All sides have different lengths | All angles are acute (less than 90°) |
| Obtuse-angled scalene triangle | All sides have different lengths | One angle is obtuse (more than 90° but less than 180°), and the other two angles are acute |
| Right-angled scalene triangle | All sides have different lengths | One angle is a right angle (exactly 90°), and the other two angles are acute |
This table provides a clear overview of the characteristics that differentiate each type of scalene triangle based on their side lengths and angle measurements.
Properties of Scalene Triangle
Scalene triangles possess several unique properties that aid in their identification:
- Unequal Sides: None of the sides in a scalene triangle are the same length.
- Unequal Angles: Each angle within a scalene triangle measures differently.
- No Line of Symmetry: A scalene triangle has no axis of symmetry due to its unequal sides and angles.
- Rotational Symmetry of Order 1: A scalene triangle has rotational symmetry of order 1, meaning it only matches its original shape once in a full 360-degree rotation.
- Angle-Side Relationship: The largest angle is opposite the longest side, while the smallest angle is opposite the shortest side.
Formulas of Scalene Triangle
To further explore the mathematical aspects of scalene triangles, let’s delve into the formulas used to calculate their area and perimeter.
Area of a Scalene Triangle
The area of any triangle, including scalene triangles, can be calculated using the formula:
Area = 1/2 * base * height
When the base and height of a scalene triangle are given, substituting these values into the formula allows us to calculate the area. The base refers to the length of one side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex.
Let’s consider an example to illustrate the application of this formula:
Example 1: Find the area of a scalene triangle with a base of 6 cm and a height of 8 cm.
Solution: Using the formula for the area of a triangle, we have:
Area = 1/2 * base * height
= 1/2 * 6 cm * 8 cm
= 24 cm²
Therefore, the area of the scalene triangle is 24 square centimeters.
In situations where the base and height of the triangle are not provided, we can use another formula known as Heron’s formula. Heron’s formula allows us to calculate the area of a scalene triangle when the lengths of all three sides are known.
Area = √(s(s - a)(s - b)(s - c))
In this formula, ‘s’ represents the semi-perimeter of the triangle, which is the sum of all three side lengths divided by 2. ‘a’, ‘b’, and ‘c’ represent the lengths of the three sides of the triangle.
Let’s consider another example to demonstrate the use of Heron’s formula:
Example 2: Calculate the area of a scalene triangle with side lengths of 5 cm, 7 cm, and 9 cm.
Solution: First, we need to calculate the semi-perimeter ‘s’ using the formula:
s = (a + b + c) / 2
= (5 cm + 7 cm + 9 cm) / 2
= 21 cm / 2
= 10.5 cm
Next, we substitute the values into Heron’s formula:
Area = √(s(s - a)(s - b)(s - c))
= √(10.5 cm * (10.5 cm - 5 cm) * (10.5 cm - 7 cm) * (10.5 cm - 9 cm))
= √(10.5 cm * 5.5 cm * 3.5 cm * 1.5 cm)
= √(404.25 cm²)
= 20.11 cm² (rounded to two decimal places)
Therefore, the area of the scalene triangle with side lengths of 5 cm, 7 cm, and 9 cm is approximately 20.11 square centimeters.
Perimeter of a Scalene Triangle
The perimeter of any triangle is the sum of the lengths of all three sides. This applies to scalene triangles as well. The formula for the perimeter of a scalene triangle is:
Perimeter = a + b + c
Where ‘a’, ‘b’, and ‘c’ represent the lengths of the three sides of the triangle.
Let’s consider an example to calculate the perimeter of a scalene triangle:
Example 3: Find the perimeter of a scalene triangle with side lengths of 6 cm, 8 cm, and 10 cm.
Solution: Using the formula for the perimeter of a triangle, we have:
Perimeter = a + b + c
= 6 cm + 8 cm + 10 cm
= 24 cm
Therefore, the perimeter of the scalene triangle with side lengths of 6 cm, 8 cm, and 10 cm is 24 cm.
Understanding these formulas enables us to calculate the area and perimeter of scalene triangles, providing valuable insights into their geometric properties.
Angle Sum Property of a Triangle
The sum of the measures of all three interior angles of any triangle, including scalene triangles, is always equal to 180 degrees. This property, known as the angle sum property of a triangle, is a fundamental concept in geometry.
Let’s consider an example to illustrate the angle sum property of a scalene triangle:
Example 4: In a scalene triangle ABC, angle A measures 50 degrees, angle B measures 70 degrees. Find the measure of angle C.
Solution: According to the angle sum property of a triangle, the sum of the measures of all three interior angles is 180 degrees. Therefore, we can calculate the measure of angle C as follows:
Measure of angle C = 180 degrees - Measure of angle A - Measure of angle B
= 180 degrees - 50 degrees - 70 degrees
= 60 degrees
Hence, the measure of angle C in the scalene triangle is 60 degrees.
The angle sum property of a triangle holds true for all triangles, regardless of their type or side lengths. It is a fundamental concept that helps us understand the relationships between the angles of a triangle.
Measuring Scalene Triangles
Measuring scalene triangles involves determining the lengths of their sides and the measures of their angles. This information is critical in understanding and classifying triangles based on their properties.
To measure the sides of a scalene triangle, we can use a ruler or a measuring tape. By comparing the lengths of the three sides, we can determine whether the triangle is scalene or not. In a scalene triangle, no two sides are equal in length.
To measure the angles of a scalene triangle, we can use a protractor. Place the protractor on each vertex of the triangle and align the base of the protractor with one side. Read the measurement on the protractor to determine the measure of each angle. In a scalene triangle, each angle has a different measurement.
By accurately measuring the sides and angles of a scalene triangle, we can gather essential information about its properties and further analyze its geometric characteristics.
Difference Between Scalene, Isosceles, and Equilateral Triangles
Triangles can be classified into different types based on the lengths of their sides. The main types of triangles are scalene, isosceles, and equilateral triangles. Understanding the differences between these types is crucial in geometry.
- Scalene Triangle: A scalene triangle is a triangle with three unequal side lengths. In a scalene triangle, all three sides have different measurements, and all three angles are different as well.
- Isosceles Triangle: An isosceles triangle is a triangle with two equal side lengths and two equal angles. The third side and angle in an isosceles triangle are different from the other two.
- Equilateral Triangle: An equilateral triangle is a triangle with three equal side lengths and three equal angles. All angles in an equilateral triangle measure 60 degrees, and all sides have the same length.
The key difference between these types of triangles lies in the equality or inequality of their side lengths. Scalene triangles have no equal sides, isosceles triangles have two equal sides, and equilateral triangles have three equal sides.
Understanding these distinctions enables us to classify and analyze triangles based on their characteristics and properties.
Difference Between Scalene, Isosceles, and Equilateral Triangles Table
To summarize the differences between scalene, isosceles, and equilateral triangles, refer to the table below:
| Triangle Type | Sides | Angles |
|---|---|---|
| Equilateral Triangle | All sides are equal | All angles are equal (60° each) |
| Isosceles Triangle | Two sides are equal | The angles opposite the equal sides are equal |
| Scalene Triangle | All sides are different | All angles are different |
This table provides a concise overview of the distinctions between scalene, isosceles, and equilateral triangles based on their side lengths and angle measurements.
Frequently Asked Questions About Scalene Triangle
How to Identify Scalene Triangles Using the Distance Formula?
The distance formula can be used to identify scalene triangles by calculating the lengths of their sides. The distance formula is derived from the Pythagorean theorem and is given by:
Distance = √((x2 - x1)² + (y2 - y1)²)
To use the distance formula, you need the coordinates of the vertices of the triangle. By calculating the distances between the vertices, you can determine if all three sides have different lengths, indicating a scalene triangle.
What are the Different Classifications of Triangles?
Triangles can be classified based on their side lengths and angle measurements. The main classifications of triangles are:
- Scalene Triangle: A triangle with three different side lengths and three different angle measurements.
- Isosceles Triangle: A triangle with two equal side lengths and two equal angle measurements.
- Equilateral Triangle: A triangle with three equal side lengths and three equal angle measurements.
Knowing these classifications allows us to identify and categorize different types of triangles based on their properties.
What are Examples of Side Lengths that Form a Scalene Triangle?
Any combination of three different side lengths can form a scalene triangle. For example, side lengths of 5 cm, 7 cm, and 9 cm or side lengths of 3 inches, 6 inches, and 8 inches can both form scalene triangles. As long as all three sides have different lengths, the triangle will be classified as scalene.
How to Find the Missing Side Length of a Scalene Triangle?
To find the missing side length of a scalene triangle, you need to use the properties of triangles and the given information. If you know the lengths of two sides and the measure of the included angle, you can use the Law of Cosines to find the missing side length. Alternatively, if you know the lengths of two sides and the measure of the non-included angle, you can use the Law of Sines to find the missing side length.
Can Scalene Triangles be Obtuse?
Yes, scalene triangles can be obtuse. An obtuse triangle is a triangle with one angle greater than 90 degrees. In a scalene triangle, any of the three angles can be obtuse, as long as the other two angles are acute.
These frequently asked questions provide additional insights into the properties and characteristics of scalene triangles, helping us understand them better in different contexts.
Solved Examples on How to Use the Scalene Triangle
Now, let’s work through some examples to illustrate how to apply the concepts and formulas related to scalene triangles in problem-solving scenarios.
Example 1: Finding the Area of a Scalene Triangle
Let’s find the area of a scalene triangle when the base and height are given.
Problem: Find the area of a scalene triangle with a base of 8 cm and a height of 12 cm.
Solution: Using the formula for the area of a triangle, we have:
Area = 1/2 * base * height
= 1/2 * 8 cm * 12 cm
= 48 cm²
Therefore, the area of the scalene triangle is 48 square centimeters.
Example 2: Calculating the Perimeter of a Scalene Triangle
Let’s calculate the perimeter of a scalene triangle when the lengths of all three sides are given.
Problem: Find the perimeter of a scalene triangle with side lengths of 6 cm, 8 cm, and 10 cm.
Solution: Using the formula for the perimeter of a triangle, we have:
Perimeter = a + b + c
= 6 cm + 8 cm + 10 cm
= 24 cm
Therefore, the perimeter of the scalene triangle is 24 cm.
Example 3: Determining the Measure of an Angle in a Scalene Triangle
Let’s determine the measure of an angle in a scalene triangle when the measures of the other two angles are known.
Problem: In a scalene triangle, angle A measures 50 degrees, and angle B measures 70 degrees. Find the measure of angle C.
Solution: According to the angle sum property of a triangle, the sum of the measures of all three interior angles is always 180 degrees. Therefore, we can calculate the measure of angle C as follows:
Measure of angle C = 180 degrees - Measure of angle A - Measure of angle B
= 180 degrees - 50 degrees - 70 degrees
= 60 degrees
Hence, the measure of angle C in the scalene triangle is 60 degrees.
These solved examples demonstrate the application of formulas and concepts related to scalene triangles in various problem-solving scenarios. They showcase how to use the formulas for area and perimeter, as well as the angle sum property, to solve problems involving scalene triangles.
How Kunduz Can Help You Learn Scalene Triangle?
At Kunduz, we understand the importance of mastering geometric concepts like scalene triangles. Our comprehensive learning resources, interactive lessons, and practice exercises are designed to help students develop a deep understanding of geometry and excel in their academic pursuits.
Through our user-friendly platform, students can access a wide range of educational materials, including video tutorials, step-by-step explanations, and interactive quizzes. Whether you’re learning about the properties of scalene triangles or exploring advanced geometric concepts, Kunduz provides the tools and resources to support your learning journey.
With Kunduz, you can learn at your own pace, review difficult concepts, and track your progress. Our platform is accessible anytime, anywhere, making it convenient for students to engage with their studies and enhance their understanding of geometry.
Join Kunduz today and unlock your full potential in geometry. Let us guide you through the intricate world of scalene triangles and empower you to succeed in your mathematical endeavors.
