In the world of mathematics, linear equations play a crucial role in understanding the relationship between variables. One of the most commonly used forms of writing the equation of a straight line is the slope-intercept form. This form allows us to easily identify the slope and y-intercept of a line, providing valuable information about its characteristics and behavior.

Understanding and mastering the slope-intercept form is essential for students studying algebra and geometry. In this article, we will explore the concept of slope-intercept form, its formula, derivation, and various applications. By the end, you will have a solid understanding of how to write equations in slope-intercept form and interpret their meaning.

So, let’s dive into the world of slope-intercept form and unlock the mysteries of linear equations!

What is Slope Intercept Form?

Slope-intercept form is a way of writing the equation of a straight line in the form: y = mx + b. In this equation, m represents the slope of the line, and b represents the y-intercept, which is the point where the line intersects the y-axis.

The slope (m) of a line is the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. It indicates the steepness or incline of the line. The y-intercept (b) is the value of y when x is equal to 0, or the point where the line crosses the y-axis.

By using the slope-intercept form, we can easily identify the slope and y-intercept of a line, which provides valuable insights into its behavior and characteristics. This form is particularly useful for graphing lines, solving systems of equations, and making predictions based on the equation of a line.

Now that we have a basic understanding of slope-intercept form, let’s explore its formula and how to derive it.

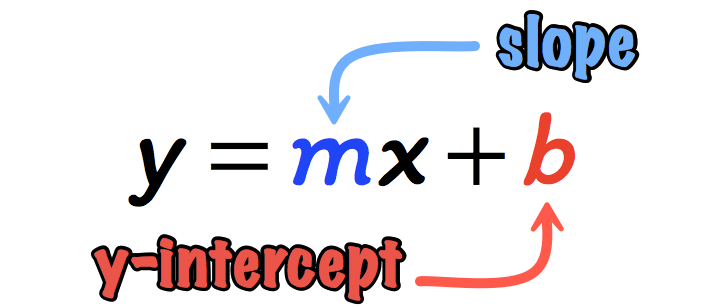
What is the Slope Intercept Form of a Straight Line?

The slope-intercept form of a straight line is an equation that represents the relationship between x and y in terms of their values, slope, and y-intercept. It is written as y = mx + b, where:

• y is the dependent variable (usually representing the vertical axis).
• x is the independent variable (usually representing the horizontal axis).
• m is the slope of the line, indicating its steepness or incline.
• b is the y-intercept, representing the point where the line crosses the y-axis.

The slope-intercept form is widely used because it provides a clear and concise representation of a line’s equation. It allows us to easily interpret the slope (m) as the rate of change between x and y and the y-intercept (b) as the starting point of the line.

By utilizing this form, we can graph lines, solve systems of equations, and make predictions based on the equation of a line. It is a powerful tool in the field of algebra and geometry, enabling us to analyze and understand linear relationships between variables.

Now that we have defined slope-intercept form, let’s delve into its formula and how it can be derived.

What is the Point Slope Form?

Before we explore the formula and derivation of the slope-intercept form, it is essential to understand another form of writing linear equations: the point-slope form.

The point-slope form of a linear equation is given by y - y1 = m(x - x1), where:

• (x1, y1) is a point on the line.
• m is the slope of the line.

This form allows us to write the equation of a line when we are given a point (x1, y1) and the slope (m). It is particularly useful when we have specific data points and need to find the equation of a line passing through those points.

By using the point-slope form, we can easily determine the equation of a line without relying on the y-intercept. It provides a versatile and flexible approach to writing linear equations and is a valuable tool in analyzing and interpreting real-world data.

Now that we understand the point-slope form, let’s move on to exploring the formula and derivation of the slope-intercept form.

Slope Intercept Formula

The slope-intercept form of a linear equation is written as y = mx + b, where:

• y represents the dependent variable (usually the vertical axis).
• x represents the independent variable (usually the horizontal axis).
• m represents the slope of the line.
• b represents the y-intercept, the point where the line crosses the y-axis.

This form provides a clear and concise representation of a line’s equation, allowing us to easily interpret its slope and y-intercept. The slope (m) represents the rate of change between x and y, while the y-intercept (b) represents the starting point of the line.

To determine the equation of a line in slope-intercept form, we need to know the slope (m) and the y-intercept (b). With this information, we can write the equation and graph the line.

The slope-intercept form is widely used in various applications, such as graphing lines, solving systems of equations, and making predictions based on the equation of a line. Its simplicity and versatility make it an essential tool in algebra and geometry.

Now that we understand the slope-intercept form, let’s explore the coefficients in this equation and their significance.

The Coefficients in Slope-Intercept Form

The slope-intercept form of a linear equation, y = mx + b, has two coefficients: m and b. These coefficients play a crucial role in determining the characteristics and behavior of the line represented by the equation.

The coefficient m represents the slope of the line. It determines the steepness or incline of the line, indicating the rate of change between x and y. A positive slope indicates an upward incline, while a negative slope indicates a downward incline. The magnitude of the slope represents the degree of steepness.

The coefficient b represents the y-intercept of the line. It indicates the point where the line crosses the y-axis, which occurs when x is equal to 0. The y-intercept is a significant value as it provides information about the starting point of the line and its position on the y-axis.

By understanding the significance of these coefficients, we can interpret the slope-intercept form and gain insights into the characteristics of the line it represents.

Now that we have explored the coefficients in slope-intercept form, let’s delve into the derivation of this equation and understand how it can be derived from other forms of linear equations.

Derivation of the Formula for Slope-Intercept Form

The slope-intercept form of a linear equation, y = mx + b, can be derived from other forms of linear equations, such as the point-slope form and standard form.

To derive the slope-intercept form, let’s start with the point-slope form of a linear equation: y - y1 = m(x - x1). In this form, (x1, y1) represents a point on the line, and m represents the slope.

Next, let’s rearrange the equation to isolate y:

y - y1 = m(x - x1)
y = mx - mx1 + y1

We can rewrite this as:

y = mx + (y1 - mx1)

By comparing this equation to the slope-intercept form, y = mx + b, we can see that b is equal to (y1 - mx1). Therefore, we can derive the slope-intercept form from the point-slope form by identifying the y-intercept and slope.

Additionally, we can derive the slope-intercept form from the standard form of a linear equation: Ax + By = C. By rearranging the terms and solving for y, we can express the equation in slope-intercept form.

Now that we understand the derivation of the slope-intercept form, let’s explore how to find the slope-intercept form of a linear equation given different sets of information.

How to Find the Slope-Intercept Form (Equation of a Straight Line)

To find the slope-intercept form (equation of a straight line), we need different sets of information depending on the scenario. Let’s explore three common scenarios and the steps involved in finding the slope-intercept form in each case.

Scenario 1: Two Points

Given two points (x1, y1) and (x2, y2) on a line, we can find the slope-intercept form using the following steps:

Step 1: Calculate the slope m using the formula:

m = (y2 - y1) / (x2 - x1)

Step 2: Choose one of the points (let’s say (x1, y1)) and substitute the values of m and the coordinates into the slope-intercept form equation:

y = mx + b
y1 = m * x1 + b

Step 3: Solve for b by rearranging the equation:

b = y1 - m * x1

Step 4: Substitute the values of m and b into the slope-intercept form equation to obtain the final equation of the line.

Scenario 2: Slope and Y-Intercept

Given the slope m and the y-intercept (0, b), we can find the slope-intercept form using the following steps:

Step 1: Substitute the values of m and b into the slope-intercept form equation:

y = mx + b

Step 2: Simplify the equation to obtain the final equation of the line.

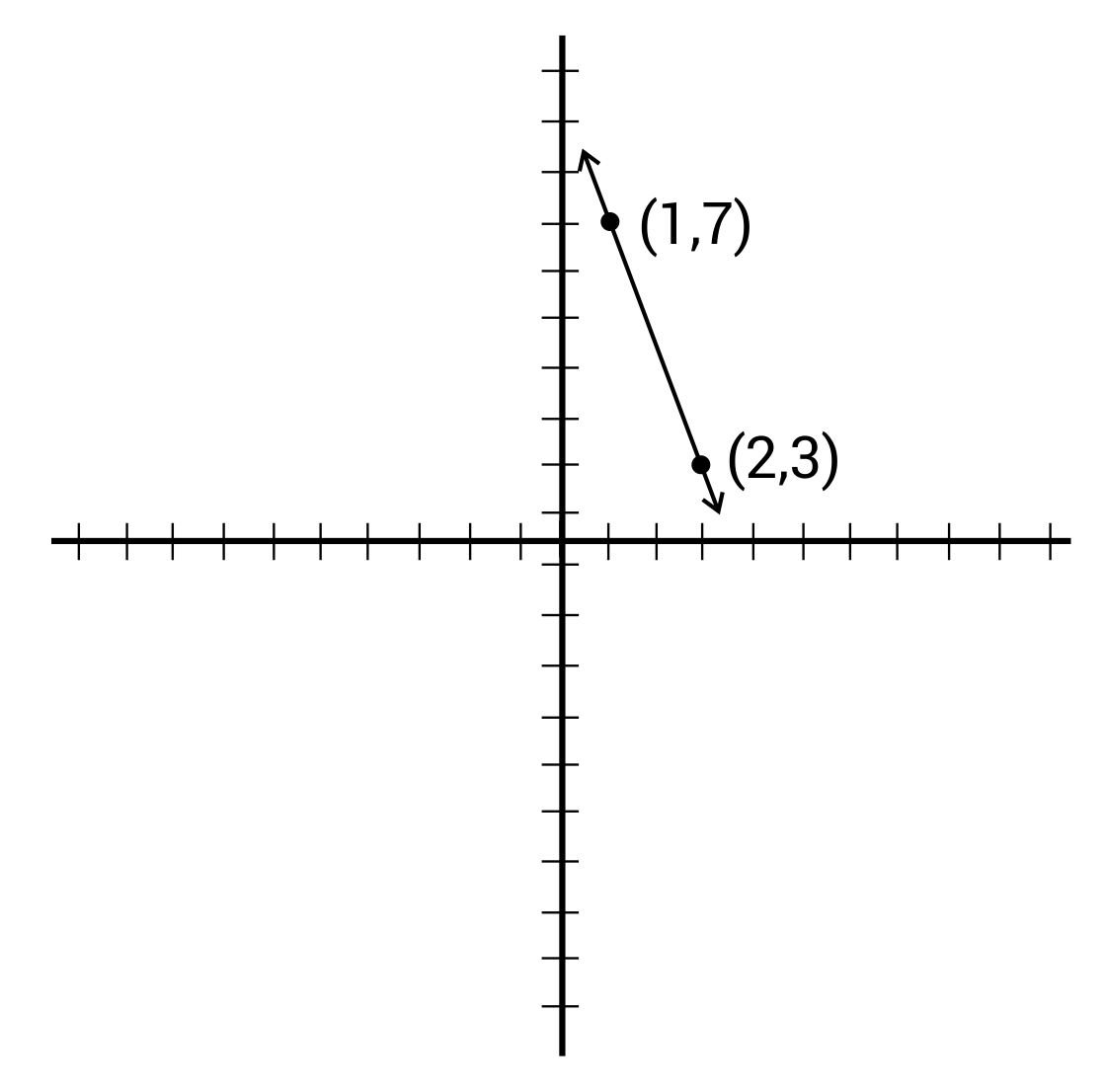
Scenario 3: Graph

Given a graph of a line, we can find the slope-intercept form using the following steps:

Step 1: Choose two points on the line and determine their coordinates.

Step 2: Calculate the slope m using the formula:

m = (y2 - y1) / (x2 - x1)

Step 3: Choose one of the points (let’s say (x1, y1)) and substitute the values of m and the coordinates into the slope-intercept form equation:

y = mx + b
y1 = m * x1 + b

Step 4: Solve for b by rearranging the equation:

b = y1 - m * x1

Step 5: Substitute the values of m and b into the slope-intercept form equation to obtain the final equation of the line.

By following these steps, we can find the slope-intercept form for any given line, enabling us to understand its characteristics and behavior.

Now that we know how to find the slope-intercept form, let’s explore how to convert the standard form of a linear equation to slope-intercept form.

Converting Standard Form to Slope-Intercept Form

Converting a linear equation from standard form (Ax + By = C) to slope-intercept form (y = mx + b) involves rearranging the terms to isolate y.

Let’s go through the steps to convert a standard form equation to slope-intercept form:

Step 1: Start with the equation in standard form: Ax + By = C.

Step 2: Subtract Ax from both sides of the equation:

By = -Ax + C

Step 3: Divide both sides of the equation by B to isolate y:

y = (-A / B)x + (C / B)

Step 4: Simplify the equation to obtain the final equation in slope-intercept form.

By following these steps, we can convert any linear equation from standard form to slope-intercept form, which provides a clearer representation of the line’s equation and its characteristics.

Now that we understand how to convert standard form to slope-intercept form, let’s explore the graphing of slope-intercept form equations and their significance.

Slope-Intercept Form Graph

Graphing equations in slope-intercept form (y = mx + b) allows us to visualize the line represented by the equation and understand its characteristics.

To graph a line using slope-intercept form, we follow these steps:

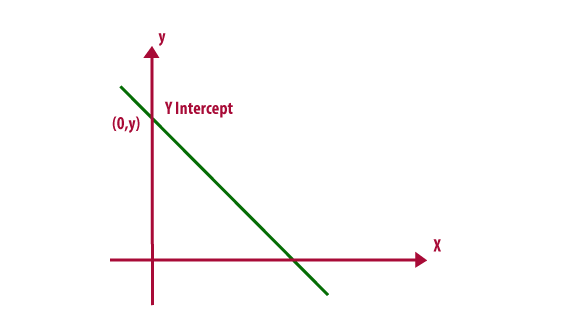
Step 1: Identify the y-intercept (b), which represents the point where the line crosses the y-axis. This point is denoted as (0, b).

Step 2: Plot the y-intercept on the graph.

Step 3: Use the slope (m) to determine additional points on the line. The slope represents the rate of change between x and y and determines the incline or decline of the line.

Step 4: Plot the additional points on the graph.

Step 5: Connect the points to form a line.

By following these steps, we can graph lines represented by equations in slope-intercept form. Graphing lines allows us to visualize and understand their behavior, incline, decline, and intersection with other lines or curves.

Now that we have explored graphing equations in slope-intercept form, let’s examine other forms of linear equations and their relationship to slope-intercept form.

Slope-Intercept and Point-Slope Forms of a Linear Equation

While slope-intercept form is a commonly used representation of linear equations, it is not the only form available. Another significant form is the point-slope form, which provides a way to express the equation of a line using a single point and the slope.

The point-slope form of a linear equation is given by y - y1 = m(x - x1), where (x1, y1) represents a point on the line, and m represents the slope.

The point-slope form is particularly useful when we have a specific point and the slope and need to determine the equation of a line passing through that point. It provides a versatile and flexible approach to writing linear equations and enables us to analyze and interpret real-world data.

While slope-intercept form and point-slope form are distinct representations, they are closely related. In fact, the slope-intercept form can be derived from the point-slope form by rearranging the equation and isolating y.

Understanding the relationship between these two forms allows us to switch between them as needed, depending on the given information and the required representation. Both forms have their advantages and applications, making them valuable tools in the study of linear equations.

Now that we have explored the relationship between slope-intercept and point-slope forms, let’s take a step back and examine the concept of a linear equation.

What is a Linear Equation?

A linear equation represents a relationship between two variables (x and y) that can be expressed as a straight line on a graph. It is a fundamental concept in algebra and provides a powerful tool for analyzing and understanding the relationship between variables.

A linear equation can be written in various forms, such as slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), or standard form (Ax + By = C). Each form provides a different perspective on the equation and its characteristics.

The slope-intercept form, as we have explored in detail, is particularly useful for graphing lines, determining the slope and y-intercept, and making predictions based on the equation of a line.

Linear equations are prevalent in various fields of study, including physics, engineering, economics, and more. They provide a foundation for understanding and analyzing relationships between variables and have applications in real-world problem solving.

Now that we have a solid understanding of linear equations, let’s delve into some solved examples to further solidify our knowledge of slope-intercept form.

Solved Examples on Slope-Intercept Form

Example 1: Find the slope-intercept form of the line passing through the points (2, 5) and (4, 9).

Step 1: Calculate the slope m using the formula:

m = (y2 - y1) / (x2 - x1)
m = (9 - 5) / (4 - 2)
m = 4 / 2
m = 2

Step 2: Choose one of the points (let’s use (2, 5)) and substitute the values of m and the coordinates into the slope-intercept form equation:

y = mx + b
5 = 2 * 2 + b
5 = 4 + b
b = 5 - 4
b = 1

Step 3: Substitute the values of m and b into the slope-intercept form equation to obtain the final equation of the line:

y = mx + b
y = 2x + 1

Therefore, the slope-intercept form of the line passing through the points (2, 5) and (4, 9) is y = 2x + 1.

Example 2: Convert the equation 3x - 2y = 6 to slope-intercept form.

Step 1: Rearrange the equation to isolate y:

3x - 2y = 6
-2y = -3x + 6

Step 2: Divide both sides of the equation by -2 to solve for y:

y = (3/2)x - 3

Therefore, the equation 3x - 2y = 6 in slope-intercept form is y = (3/2)x - 3.

Example 3: Graph the equation y = -2x + 4 in the coordinate plane.

To graph the equation y = -2x + 4, we need to plot a few points and connect them to form a line.

Let’s choose a few values for x and calculate the corresponding y values:

• When x = 0, y = -2(0) + 4 = 4. So, one point on the line is (0, 4).
• When x = 1, y = -2(1) + 4 = 2. So, another point on the line is (1, 2).

Plot these points on the coordinate plane and connect them with a straight line. The resulting line represents the graph of the equation y = -2x + 4.

How Kunduz Can Help You Learn Slope-Intercept Form?

At Kunduz, we understand the importance of mastering slope-intercept form and its applications in algebra and geometry. We are committed to providing you with the resources and support you need to excel in your mathematical journey.

Through our comprehensive online platform, you can access a wide range of interactive lessons, practice problems, and step-by-step tutorials specifically designed to help you understand and apply slope-intercept form. Our experienced mathematics teachers and tutors are available to answer your questions, provide personalized guidance, and ensure that you have a solid grasp of the concept.

With Kunduz, you can learn at your own pace, review challenging topics, and track your progress as you navigate through the world of slope-intercept form. Our user-friendly interface and engaging content make learning mathematics enjoyable and accessible to students of all levels.

Whether you’re preparing for an exam, seeking additional support, or simply looking to enhance your mathematical skills, Kunduz has the resources and expertise to help you succeed. Join our community of learners today and unlock the power of slope-intercept form!

In conclusion, slope-intercept form is a powerful tool in understanding and analyzing linear equations. By mastering this form, you can easily identify the slope and y-intercept of a line, graph equations, solve systems of equations, and make predictions based on the equation of a line. With Kunduz as your companion, you can confidently navigate the world of slope-intercept form and unlock the secrets of linear equations. So, let’s embark on this mathematical journey together and achieve academic excellence!