In the world of mathematics, equations play a crucial role in solving problems and finding unknown values. An equation is a mathematical statement that contains an equal sign (=), indicating that the expressions on both sides of the equal sign are equal. Solving an equation involves finding the value of the unknown variable that satisfies the equation.
Equations can come in various forms, such as linear equations, quadratic equations, rational equations, radical equations, and more. Each type of equation requires specific methods and techniques to find the solution. In this article, we will explore different methods for solving equations and provide examples to illustrate the process.
What is an Equation?
An equation is a statement that asserts the equality of two expressions. It consists of two sides, the left-hand side (LHS) and the right-hand side (RHS), separated by an equal sign (=). The value of the unknown variable is determined by finding the solution that makes both sides of the equation equal.
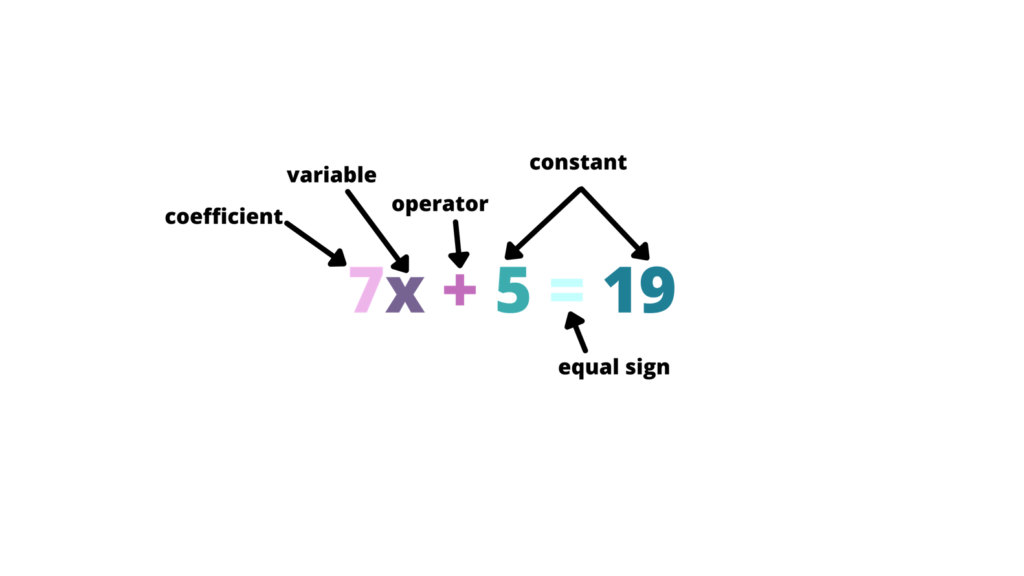
Terminologies of Simple Equations
Before diving into the methods of solving equations, let’s familiarize ourselves with some key terminologies:
- Variables: Variables are symbols that represent unknown values in an equation. They are typically denoted by letters such as x, y, or z.
- Constants: Constants are fixed numerical values that do not change. They are represented by numbers such as 1, 2, 3, and so on.
- Roots or Solutions: The roots or solutions of an equation are the values of the variable that satisfy the equation, making both sides equal.
How To Solve an Equation?
Solving an equation involves a systematic approach to find the value of the unknown variable that satisfies the equation. There are various methods and techniques that can be used depending on the type of equation. In this section, we will discuss some common methods for solving equations.
Solving Equations of One Variable
Linear equations with one variable are the simplest type of equations. They can be represented in the form of ax + b = 0, where a, b, and x are real numbers. To solve such equations, we follow a series of steps:
Step 1: Simplify the Equation
If there are any parentheses or terms that can be simplified, apply the necessary operations to simplify both sides of the equation.
Step 2: Combine Like Terms
Combine like terms on both sides of the equation to simplify further.
Step 3: Isolate the Variable
Bring the variable terms to one side of the equation and the constant terms to the other side using addition, subtraction, multiplication, or division operations. The goal is to isolate the variable on one side of the equation.
Step 4: Make the Coefficient of the Variable 1
If the coefficient of the variable is not 1, use multiplication or division to make it 1. This simplifies the equation and makes it easier to solve.
Step 5: Solve for the Variable
After isolating the variable, perform the necessary operations to solve for the variable. The resulting value is the solution to the equation.
Let’s consider an example to illustrate the steps involved in solving a linear equation of one variable:
Example: Solve the equation 3(x + 4) = 24 + x.
Step 1: Simplify the Equation 3x + 12 = 24 + x
Step 2: Combine Like Terms 3x – x = 24 – 12 2x = 12
Step 3: Isolate the Variable 2x/2 = 12/2 x = 6
In this example, the solution to the equation is x = 6.
Solving Linear Equations
Linear equations involve two or more variables and can have multiple solutions. There are different methods for solving linear equations, such as the graphical method, elimination method, substitution method, cross multiplication method, matrix method, and determinants method. Let’s explore these methods in more detail:
Graphical Method of Solving Linear Equations
The graphical method involves graphing the equations on a coordinate system and finding the point of intersection. The point of intersection represents the solution to the equations. This method is useful for solving linear equations involving two variables.
To solve the equations graphically, plot the equations on the same coordinate system and find the point of intersection. The x-coordinate and y-coordinate of the intersection point represent the solution to the equations.
Elimination Method of Solving Linear Equations
The elimination method involves eliminating one variable by adding or subtracting the equations. This method is useful for solving systems of linear equations involving two or more variables.
To use the elimination method, multiply the equations by appropriate factors to make the coefficients of one variable the same. Then, add or subtract the equations to eliminate that variable. Solve the resulting equation to find the value of the remaining variable.
Substitution Method of Solving Linear Equations
The substitution method involves solving one equation for one variable and substituting the solution into the other equation. This method is useful for solving systems of linear equations involving two or more variables.
To use the substitution method, solve one equation for one variable in terms of the other variables. Substitute this solution into the other equation and solve for the remaining variables.
Cross Multiplication Method of Solving Linear Equations
The cross multiplication method is used to solve linear equations involving fractions. This method involves cross-multiplying the fractions to eliminate the denominators and solve for the variables.
To use the cross multiplication method, multiply the numerator of one fraction by the denominator of the other fraction, and vice versa. Equate the two resulting products and solve for the variables.
Matrix Method of Solving Linear Equations
The matrix method involves representing the equations as a matrix equation and solving it using matrix operations. This method is useful for solving systems of linear equations involving two or more variables.
To use the matrix method, represent the equations in matrix form and solve the matrix equation using matrix operations such as row operations and Gaussian elimination.
Determinants Method of Solving Linear Equations (Cramer’s Rule)
The determinants method, also known as Cramer’s Rule, uses determinants to solve systems of linear equations. This method involves calculating the determinants of matrices and using them to find the solutions.
To use Cramer’s Rule, calculate the determinants of the coefficient matrix and the augmented matrix. Then, divide the determinants to find the values of the variables.
Solving Quadratic Equation
Quadratic equations are equations of degree two and can have two solutions. They can be represented in the form of ax^2 + bx + c = 0, where a, b, and c are real numbers. There are different methods for solving quadratic equations, such as completing the square, factorization, and using the quadratic formula.
Solving Quadratic Equation by Completing Squares Method
The completing squares method involves transforming the quadratic equation into a perfect square trinomial and solving for the variable. This method is useful for solving quadratic equations that cannot be easily factored.
To use the completing squares method, rewrite the quadratic equation in the form of (x + p)^2 = q and solve for the variable.
Solving Quadratic Equation by Factorization Method
The factorization method involves factoring the quadratic equation and solving for the variable. This method is useful for solving quadratic equations that can be factored.
To use the factorization method, factor the quadratic equation into two binomials and set each binomial equal to zero. Solve the resulting linear equations to find the values of the variable.
Solving Quadratic Equation by Formula Method
The formula method, also known as the quadratic formula, involves using the quadratic formula to find the solutions of the quadratic equation. The quadratic formula is x = (-b ± √(b^2 – 4ac))/(2a), where a, b, and c are the coefficients of the quadratic equation.
To use the quadratic formula, substitute the values of a, b, and c into the formula and solve for the variable.
Solving Rational Equation
Rational equations involve fractions and can have multiple solutions. They can be solved by finding the common denominator and eliminating the fractions.
To solve rational equations, find the common denominator of the fractions and multiply both sides of the equation by the common denominator to eliminate the fractions. Solve the resulting equation to find the values of the variable.
Solving Radical Equation
Radical equations involve radicals, such as square roots or cube roots, and can have multiple solutions. They can be solved by isolating the radical term and raising both sides of the equation to an appropriate power.
To solve radical equations, isolate the radical term on one side of the equation and raise both sides of the equation to the appropriate power to eliminate the radical. Solve the resulting equation to find the values of the variable.
Solved Examples on Solving an Equation
Now, let’s apply the methods and techniques discussed above to solve some examples of equations.
Example 1: Solve the equation 4x + 7 = 31.
Step 1: Simplify the Equation 4x + 7 = 31
Step 2: Combine Like Terms 4x = 31 – 7 4x = 24
Step 3: Isolate the Variable 4x/4 = 24/4 x = 6
The solution to the equation is x = 6.
Example 2: Solve the equation (2x – 5)/3 = 4.
Step 1: Simplify the Equation (2x – 5)/3 = 4
Step 2: Isolate the Variable Multiply both sides of the equation by 3 to eliminate the fraction. 2x – 5 = 12
Step 3: Combine Like Terms 2x = 12 + 5 2x = 17
Step 4: Isolate the Variable Divide both sides of the equation by 2 to solve for x. 2x/2 = 17/2 x = 8.5
The solution to the equation is x = 8.5.
Example 3: Solve the equation √(x + 2) = 5.
Step 1: Isolate the Radical Term Square both sides of the equation to eliminate the square root. (x + 2) = 5^2 x + 2 = 25
Step 2: Isolate the Variable Subtract 2 from both sides of the equation to solve for x. x = 25 – 2 x = 23
The solution to the equation is x = 23.
These examples demonstrate the application of different methods and techniques to solve equations and find the values of the unknown variables.
How Kunduz Can Help You Learn Solving an Equation?
At Kunduz, we understand the importance of mastering the skill of solving equations. That’s why we offer comprehensive online courses and resources to help you learn and improve your problem-solving abilities. Our expert instructors guide you through step-by-step explanations and provide practice problems to reinforce your understanding.
With Kunduz, you can access interactive lessons, video tutorials, and practice quizzes to enhance your learning experience. Whether you’re a student preparing for exams or an individual looking to improve your mathematical skills, Kunduz is here to support your academic journey.
Join Kunduz today and unlock your potential in solving equations and other mathematical concepts. With our user-friendly platform and expert guidance, you’ll gain the confidence and skills needed to excel in mathematics.
