Spherical coordinates are a unique system of coordinates that facilitate the identification of a point’s location in three-dimensional space. This system is widely employed in a variety of scientific fields, including physics and mathematics, due to its ability to simplify complex calculations involving three-dimensional objects. In this article, we will explore the spherical coordinate system in detail, including its definition, formulas, and conversion methods. We will also discuss its applications and provide examples to illustrate its practical use.
An Introduction to Spherical Coordinates
Spherical coordinates are a robust tool to represent a point’s position in three-dimensional space. This coordinate system is characterized by a set of three values, namely radial distance, polarization angle, and azimuthal angle. These three values together formulate a unique identifier for any point in three-dimensional space.
What are Spherical Coordinates?
Spherical Coordinates are an ordered set of three-dimensional values, namely radial distance, polar angle, and azimuthal angle. The table below provides an overview of these components.
| Coordinate | Name | Range | Definition |
|---|---|---|---|
| r | Radial Distance | r ≥ 0 | Distance from the origin to the point |
| θ | Polar Angle | 0 ≤ θ ≤ 180° or 0 rad ≤ θ ≤ π rad | Angle from the positive z-axis |
| φ | Azimuthal Angle | 0° ≤ φ < 360° or 0 rad ≤ φ < 2π rad | Angle from the positive x-axis in xy-plane |
What is a Spherical Coordinate System?
The spherical coordinate system is a three-dimensional coordinate system that uses three coordinates to determine the position of a point in space. It is particularly useful in fields where the problem or system exhibits spherical symmetry. In this system, a point’s location is determined by the radial distance from the point to the origin, the polar angle from the positive z-axis, and the azimuthal angle from the positive x-axis.

Spherical Coordinates Formula
In spherical coordinates, the position of a point is represented by an ordered triple ((r, θ, φ)), where ‘r’ is the radial distance from the origin to the point, ‘θ’ represents the polar angle from the positive z-axis, and ‘φ’ is the azimuthal angle from the positive x-axis.
Spherical Coordinates Conversions
Switching between different coordinate systems often requires conversion formulas. The following sections delve into the various conversion methods for spherical coordinates.
Spherical Coordinates to Cylindrical Coordinates
In the spherical coordinate system, a point’s location is defined by its radial distance, polar angle, and azimuthal angle. To convert these spherical coordinates into cylindrical coordinates, we use the following formulas:
- r = ρ sin θ
- φ = φ
- z = r cos θ
Cylindrical Coordinates to Spherical Coordinates
To convert cylindrical coordinates to spherical coordinates, we use the following equations:
- ρ = √(r² + z²)
- θ = arctan(r / z)
- φ = φ
Spherical Coordinates to Cartesian Coordinates
Converting from spherical to Cartesian coordinates involves the following steps:
- x = ρ sin φ cos θ
- y = ρ sin φ sin θ
- z = ρ cos φ
Cartesian Coordinates to Spherical Coordinates
The conversion from Cartesian to spherical coordinates involves the following steps:
- ρ = √(x² + y² + z²)
- θ = arctan(y / x)
- φ = arccos(z / ρ)
Integration Over Length
The line element for an infinitesimal displacement from (r, θ, φ) to (r + dr, θ + dθ, φ + dφ) in spherical coordinates is:
- dl = r dr + r dθ + r sin θ dφ
Integration Over Area
The area element in spherical coordinates, often denoted as dA or dS, can be expressed as:
- dA = r² sin θ dθ dφ
Integration Over Volume
The volume element in spherical coordinates, denoted as dv, is given by:
- dv = r² sin θ dr dθ dφ
Jacobian For Spherical Coordinates
The Jacobian is a matrix that consists of first-order partial derivatives of a vector or scalar function. It plays a critical role in the transformation of spherical coordinates to other coordinate systems.
Spherical Coordinates Integral
The spherical coordinate integral is a method for integrating a function in spherical coordinates. It transforms the volume element from one coordinate system to another, which is especially beneficial when dealing with systems that demonstrate some degree of symmetry.
Divergence in Spherical Coordinates
Divergence is a vector operator that measures the magnitude of a vector field’s source or sink at a given point in space. In the context of spherical coordinates, divergence is calculated as:
- ∇ • F = (1 / r²) ∂(r² Fr) / ∂r + (1 / r sin θ) ∂(sin θ Fθ) / ∂θ + (1 / r sin θ) ∂Fφ / ∂φ
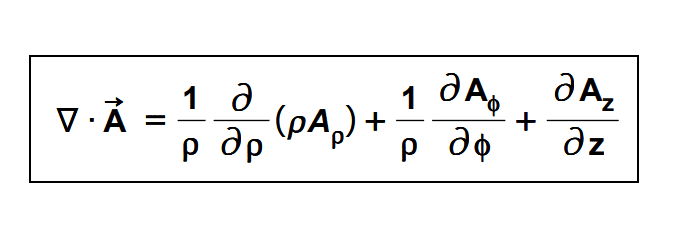
Laplacian in Spherical Coordinates
The Laplacian is a second-order differential operator that plays a crucial role in many areas of mathematics, including calculus and vector analysis. In spherical coordinates, the Laplacian of a scalar function φ(r, θ, φ) is given by:
- ∇²φ = (1 / r²) ∂ / ∂r (r² ∂φ / ∂r) + (1 / r² sin θ) ∂ / ∂θ (sin θ ∂φ / ∂θ) + (1 / r² sin² θ) ∂²φ / ∂φ²
Curl in Spherical Coordinates
In vector calculus, the curl is a vector operator that describes the infinitesimal rotation of a 3-dimensional vector field. In spherical coordinates, the curl of a vector field F = Fr r̂ + Fθ θ̂ + Fφ φ̂ is given by:
- ∇ x F = (1 / r sin θ) [ ∂ / ∂θ (sin θ Fφ) – ∂Fθ / ∂φ ] r̂ + (1 / r) [ (1 / sin θ) ∂Fr / ∂φ – ∂ / ∂r (r Fφ) ] θ̂ + (1 / r) [ ∂ / ∂r (r Fθ) – ∂Fr / ∂θ ] φ̂

Gradient in Spherical Coordinates
The gradient is a vector operator that operates on a scalar function to produce a vector pointing in the direction of the function’s greatest rate of increase. In spherical coordinates, the gradient of a scalar function φ(r, θ, φ) is given by:
- ∇φ = ∂φ / ∂r r̂ + (1 / r) ∂φ / ∂θ θ̂ + (1 / r sin θ) ∂φ / ∂φ φ̂
Volume Element in Spherical
The concept of the volume element is key in multivariable calculus and physics, particularly when integrating over a region in three-dimensional space. In spherical coordinates, the volume element, denoted as dv, is given by:
- dv = r² sin θ dr dθ dφ
Area Element in Spherical Coordinates
The area element in spherical coordinates, often denoted as dA or dS, depends on the surface on which the area is being considered. For a surface lying on a sphere of constant radius, the area element is given by:
- dA = r² sin θ dθ dφ
Uses of Spherical Coordinates System
Spherical coordinates are widely used in various fields such as physics, mathematics, engineering, and geography. They are particularly beneficial when the system or problem exhibits spherical symmetry. They are utilized in analyzing systems such as electrical and gravitational fields, global weather simulation, and three-dimensional modeling of loudspeaker output patterns.
Other applications of the spherical coordinate system include ergonomic design, where r is the arm length of a stationary person, and the angles describe the direction of the arm as it reaches out. The spherical coordinate system is also commonly used in 3D game development to rotate the camera around the player’s position.
Applications of Spherical Coordinate System
Spherical coordinates find extensive use in a myriad of applications. For instance, the geographic coordinate system, a variant of the spherical coordinate system, accurately describes a point’s latitude and longitude, making it invaluable in geography. Additionally, spherical coordinates are used in various celestial coordinate systems to measure the elevation angle from several fundamental planes.
Furthermore, spherical coordinates play a pivotal role in physics, particularly in electromagnetism and fluid dynamics. They are essential in analyzing systems exhibiting spherical symmetry, such as the potential energy field surrounding a concentrated mass or charge.
Solved Examples on Spherical Coordinates
To illustrate the practical use of spherical coordinates, let’s look at some solved examples.
Example 1: Convert the rectangular coordinate (2,2,-1) to spherical coordinates.
Solution: To convert the rectangular coordinate (2,2,-1) to spherical coordinates, we first compute the radial distance (ρ), then the azimuthal angle (φ), and finally the polar angle (θ).
- Calculating ρ: ρ = √[(2)² + (2)² + (-1)²] = √[4 + 4 + 1] = √9 = 3
- Calculating φ: φ = arctan(y / x) = arctan(2 / 2) = arctan(1) = π / 4
- Calculating θ: θ = arccos(z / ρ) = arccos(-1 / 3) ≈ 1.91 radians
Therefore, the rectangular coordinate (2,2,-1) can be expressed in spherical coordinates as (3, π/4, 1.91).
Example 2: Convert the following spherical coordinates (r, θ, φ) = (3, π/4, 1.91) to Cartesian coordinates.
Solution: To convert the given spherical coordinates to Cartesian coordinates, we utilize the following formulas:
- Calculating x: x = ρ sin φ cos θ = 3 sin(1.91) cos(π/4) ≈ 1.5
- Calculating y: y = ρ sin φ sin θ = 3 sin(1.91) sin(π/4) ≈ 1.5
- Calculating z: z = ρ cos φ = 3 cos(1.91) ≈ -1
Therefore, the spherical coordinates (3, π/4, 1.91) can be expressed in Cartesian coordinates as approximately (1.5, 1.5, -1).
How Kunduz Can Help You Learn Spherical Coordinates?
Kunduz is a revolutionary mobile app designed to assist students in their learning journey, especially in complex topics like spherical coordinates. It offers step-by-step solutions for a wide range of problems, making the learning process seamless and enjoyable. With Kunduz, you can get instant answers to your questions, understand complex concepts, and enhance your problem-solving skills. The app is a perfect companion for students who want to excel in mathematics and other scientific subjects. Download Kunduz today and take a significant stride towards academic success.
