Fractions play a significant role in mathematics as they represent parts of a whole or a collection. When we divide a whole into different equal parts, each part becomes a fraction of the whole. Subtracting fractions involves finding the difference between two or more fractions. This skill is essential in various mathematical operations and problem-solving scenarios.
In this article, we will explore the concept of subtracting fractions, including different types of fractions, such as like fractions, unlike fractions, proper fractions, improper fractions, and mixed fractions. We will also delve into the step-by-step process of subtracting fractions with like denominators, unlike denominators, and mixed numbers. Furthermore, we will discuss the addition and subtraction of fractions, simplification techniques, and properties associated with subtracting fractions. Let’s dive in and uncover the world of subtracting fractions!
For those mastering the art of subtracting fractions, our division of fractions page serves as a valuable extension. It provides essential insights into fraction operations, enhancing the understanding of mathematical principles governing both subtraction and division in the realm of fractions.
What is Subtracting Fractions?
Subtracting fractions is a mathematical operation that involves finding the difference between two or more fractions. In this operation, we subtract the numerators while keeping the denominator the same. The numerator represents the number of equal parts that are being subtracted, while the denominator represents the total number of equal parts in the whole or collection.
For example, if we have the fractions 3/4 and 1/4, subtracting them would result in (3 – 1)/4 = 2/4. This can be further simplified to 1/2, which represents the difference between the two fractions.
Subtracting fractions helps us understand how much of a fraction is being taken away from another fraction or a whole. It is a fundamental skill that allows us to solve various mathematical problems, such as comparing quantities, calculating differences, and solving real-life scenarios.
How To Subtract Fractions?
The process of subtracting fractions involves different steps depending on the type of fractions being subtracted. Let’s explore the steps for subtracting fractions with like denominators, unlike denominators, and mixed numbers.
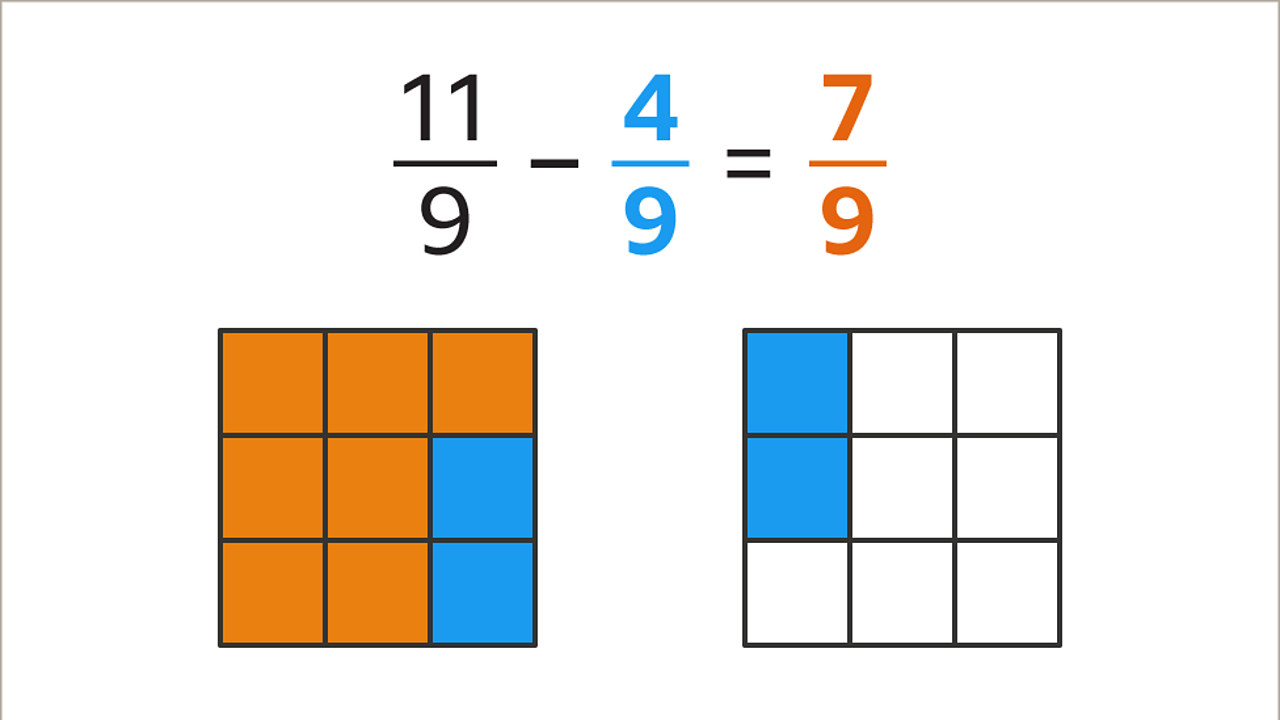
Subtracting Fractions with Like Denominators
When subtracting fractions with like denominators, the denominators are already the same, making the subtraction process more straightforward. Here are the steps to subtract fractions with like denominators:
- Keep the denominator the same.
- Subtract the numerators.
- Simplify the resulting fraction, if necessary.
For example, let’s subtract 2/5 from 3/5:
- Since the denominators are already the same, which is 5, we can directly subtract the numerators: (3 – 2) / 5 = 1/5.
The resulting fraction, 1/5, represents the difference between the two fractions.
Subtracting Fractions with Unlike Denominators
Subtracting fractions with unlike denominators requires an additional step to make the denominators the same. Here are the steps to subtract fractions with unlike denominators:
- Find the least common denominator (LCD) of the fractions.
- Convert the fractions to equivalent fractions with the LCD as the denominator.
- Subtract the numerators.
- Simplify the resulting fraction, if necessary.
For example, let’s subtract 1/3 from 1/4:
- Find the LCD of 3 and 4, which is 12.
- Convert the fractions to equivalent fractions with the LCD as the denominator:1/3 = (1 * 4) / (3 * 4) = 4/12 1/4 = (1 * 3) / (4 * 3) = 3/12
- Subtract the numerators: (4 – 3) / 12 = 1/12.
The resulting fraction, 1/12, represents the difference between the two fractions.
Subtracting Mixed Fractions with Unlike Denominators
When subtracting mixed fractions with unlike denominators, we first convert the mixed fractions into improper fractions, then follow the same steps as subtracting fractions with unlike denominators. Here are the steps:
- Convert the mixed fractions into improper fractions.
- Find the LCD of the fractions.
- Convert the fractions to equivalent fractions with the LCD as the denominator.
- Subtract the numerators.
- Simplify the resulting fraction, if necessary.
For example, let’s subtract 2 1/3 from 3 1/4:
- Convert the mixed fractions into improper fractions:2 1/3 = (2 * 3 + 1) / 3 = 7/3 3 1/4 = (3 * 4 + 1) / 4 = 13/4
- Find the LCD of 3 and 4, which is 12.
- Convert the fractions to equivalent fractions with the LCD as the denominator:7/3 = (7 * 4) / (3 * 4) = 28/12 13/4 = (13 * 3) / (4 * 3) = 39/12
- Subtract the numerators: (28 – 39) / 12 = -11/12.
The resulting fraction, -11/12, represents the difference between the two mixed fractions.
Subtracting Fractions with Whole Numbers
When subtracting fractions with whole numbers, we first convert the whole numbers into fractions, then follow the same steps as subtracting fractions with unlike denominators. Here are the steps:
- Convert the whole numbers into fractions by placing them over 1.
- Find the LCD of the fractions.
- Convert the fractions to equivalent fractions with the LCD as the denominator.
- Subtract the numerators.
- Simplify the resulting fraction, if necessary.
For example, let’s subtract 3 – 1/2:
- Convert 3 into a fraction: 3 = 3/1.
- Find the LCD of 1 and 2, which is 2.
- Convert the fractions to equivalent fractions with the LCD as the denominator:3/1 = (3 * 2) / (1 * 2) = 6/2 1/2 = 1/2 (already in the desired form)
- Subtract the numerators: (6 – 1) / 2 = 5/2.
The resulting fraction, 5/2, represents the difference between the whole number and the fraction.
How to Add and Subtract Fractions Using Cross Multiplication
Another method for subtracting fractions with unlike denominators is cross-multiplication. Here are the steps to subtract fractions using cross multiplication:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Subtract the product of the second fraction from the product of the first fraction.
- Multiply the denominators of the fractions to get the common denominator.
- Simplify the resulting fraction, if necessary.
For example, let’s subtract 1/3 from 1/4 using cross multiplication:
- Multiply the numerator of the first fraction by the denominator of the second fraction: 1 * 3 = 3.
- Multiply the numerator of the second fraction by the denominator of the first fraction: 1 * 4 = 4.
- Subtract the product of the second fraction from the product of the first fraction: 4 – 3 = 1.
- Multiply the denominators of the fractions to get the common denominator: 3 * 4 = 12.
- The resulting fraction is 1/12.
Using cross multiplication, we can subtract fractions with unlike denominators more efficiently.
Properties of Subtracting Fractions
When subtracting fractions, there are several properties that hold true:
- The order of subtraction does not affect the result. In other words, subtracting fraction A from fraction B is the same as subtracting fraction B from fraction A.
- Subtracting zero from a fraction leaves the fraction unchanged. For example, subtracting 0 from 3/4 gives us 3/4.
- Subtracting a fraction from itself results in zero. For example, subtracting 3/5 from 3/5 gives us 0.
- In subtraction, the denominator remains the same while the numerators are subtracted.
Understanding these properties can help us simplify and solve subtraction problems involving fractions more effectively.
Solved Examples on How to Use Subtracting Fractions
Let’s solve some examples that demonstrate how to subtract fractions using the methods discussed above:
Example 1: Subtract 2/3 from 5/6.
Solution: Step 1: Find the LCD of 3 and 6, which is 6. Step 2: Convert the fractions to equivalent fractions with the LCD as the denominator: 2/3 = (2 * 2) / (3 * 2) = 4/6 5/6 = (5 * 1) / (6 * 1) = 5/6 Step 3: Subtract the numerators: (5 – 4) / 6 = 1/6.
The resulting fraction is 1/6.
Example 2: Subtract 1 1/4 from 2 3/8.
Solution: Step 1: Convert the mixed fractions into improper fractions: 1 1/4 = (1 * 4 + 1) / 4 = 5/4 2 3/8 = (2 * 8 + 3) / 8 = 19/8 Step 2: Find the LCD of 4 and 8, which is 8. Step 3: Convert the fractions to equivalent fractions with the LCD as the denominator: 5/4 = (5 * 2) / (4 * 2) = 10/8 19/8 (already in the desired form) Step 4: Subtract the numerators: (19 – 10) / 8 = 9/8.
The resulting fraction is 9/8.
These examples demonstrate the step-by-step process of subtracting fractions using the methods discussed. With practice, you can become proficient in subtracting fractions and solving a variety of mathematical problems.
How Kunduz Can Help You Learn Subtracting Fractions?
At Kunduz, we understand the importance of mastering arithmetic skills such as subtracting fractions. We offer comprehensive learning materials, interactive exercises, and personalized tutoring to help students excel in mathematics.
Our experienced tutors guide students through the process of subtracting fractions, ensuring a deep understanding of the concepts and providing ample opportunities for practice. With Kunduz, you can gain the confidence and skills needed to perform subtraction operations on fractions accurately and efficiently.
Join Kunduz today and embark on a mathematical journey that will strengthen your arithmetic skills and pave the way for success in all areas of mathematics. Let us help you become a master at subtracting fractions!
