When it comes to three-dimensional shapes, the surface area plays a crucial role in determining the amount of space occupied by the shape. One such shape is a cylinder. A cylinder is a geometric solid that consists of two parallel circular bases connected by a curved surface. This shape can be found in various objects in our daily lives, such as cans, pipes, and even the well-known cylindrical containers.
The surface area of a cylinder refers to the total area covered by its outer surface. It consists of two main components: the curved surface area and the area of the circular bases. Understanding how to calculate the surface area of a cylinder is essential in various mathematical and real-world applications.
What is a Cylinder?
A cylinder is a three-dimensional shape that features two parallel circular bases connected by a curved surface. The bases are congruent and lie in parallel planes, while the curved surface forms a lateral surface that connects the bases. The axis of the cylinder is the line segment connecting the centers of the circular bases.
Cylinders can be classified into two main types: right cylinders and oblique cylinders. In a right cylinder, the axis is perpendicular to the bases, forming a right angle. In an oblique cylinder, the axis does not form a right angle with the bases.
The dimensions of a cylinder include the radius of the circular bases (r) and the height (h), which is the perpendicular distance between the bases. These dimensions play a crucial role in calculating the surface area of the cylinder.
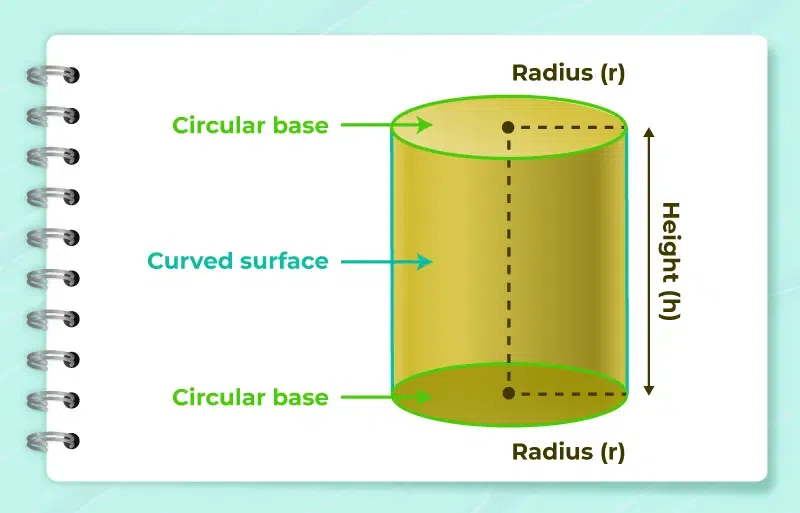
What is the Surface Area of a Cylinder?
The surface area of a cylinder refers to the total area covered by its outer surface. It consists of the area of the curved surface, also known as the lateral surface area (LSA), and the area of the two circular bases. The surface area is expressed in square units, such as square centimeters (cm²) or square meters (m²).
In mathematical terms, the surface area of a cylinder can be represented by the formula:
Surface Area of Cylinder = Curved Surface Area + Area of Circular Bases
The formula for calculating the surface area of a cylinder is given as:
Surface Area of Cylinder = 2πrh + 2πr²
where:
- π (Pi) represents the mathematical constant approximately equal to 3.14159.
- r is the radius of the circular base of the cylinder.
- h is the height of the cylinder.
By understanding and applying this formula, we can accurately determine the surface area of a cylinder.
Surface Area of a Cylinder Formulas
Curved Surface Area of Cylinder (CSA)
The curved surface area of a cylinder, also known as the lateral surface area (LSA), refers to the area formed by the curved surface of the cylinder. It does not include the area of the circular bases. The formula for calculating the curved surface area of a cylinder is:
Curved Surface Area (CSA) = 2πrh
where:
- π (Pi) represents the mathematical constant approximately equal to 3.14159.
- r is the radius of the circular base of the cylinder.
- h is the height of the cylinder.
Lateral Surface Area of Cylinder (LSA)
The lateral surface area of a cylinder is another term used to describe the curved surface area. It represents the area formed by the curved surface that connects the two circular bases. The formula for calculating the lateral surface area of a cylinder is the same as the formula for the curved surface area:
Lateral Surface Area (LSA) = 2πrh
where:
- π (Pi) represents the mathematical constant approximately equal to 3.14159.
- r is the radius of the circular base of the cylinder.
- h is the height of the cylinder.
Total Surface Area of Cylinder (TSA)
The total surface area of a cylinder refers to the sum of the areas of the curved surface and the two circular bases. It represents the complete outer surface area of the cylinder. The formula for calculating the total surface area of a cylinder is:
Total Surface Area (TSA) = 2πrh + 2πr²
where:
- π (Pi) represents the mathematical constant approximately equal to 3.14159.
- r is the radius of the circular base of the cylinder.
- h is the height of the cylinder.
By utilizing these formulas, we can accurately determine the surface area of a cylinder in various mathematical and real-world scenarios.
How to Find the Surface Area of a Cylinder?
Calculating the surface area of a cylinder involves following a step-by-step process. By applying the appropriate formulas and equations, we can accurately determine the surface area of the cylinder. Here is a step-by-step guide on how to find the surface area of a cylinder:
Step 1: Identify the Dimensions
Start by identifying the dimensions of the cylinder. Measure the radius (r) of the circular base and the height (h) of the cylinder. Ensure that the measurements are accurate and in the same unit of measurement.
Step 2: Calculate the Curved Surface Area (CSA)
To calculate the curved surface area of the cylinder, use the formula: CSA = 2πrh. Substitute the values of the radius (r) and height (h) into the formula and calculate the curved surface area.
Step 3: Calculate the Area of the Circular Bases
The area of each circular base can be calculated using the formula: Area = πr². Substitute the radius (r) into the formula and calculate the area of each circular base.
Step 4: Calculate the Total Surface Area (TSA)
To calculate the total surface area of the cylinder, use the formula: TSA = CSA + 2 × Area of Circular Bases. Add the curved surface area (CSA) calculated in step 2 to twice the area of one circular base calculated in step 3.
Step 5: Simplify and Round
Simplify the equation obtained in step 4 and round the final result to the desired level of precision. Ensure that the units of measurement are consistent throughout the calculation.
By following these steps, you can easily find the surface area of a cylinder and obtain an accurate measurement of the area covered by its outer surface.
Differences Between TSA and CSA of Cylinder
When discussing the surface area of a cylinder, it is important to understand the differences between the total surface area (TSA) and the curved surface area (CSA). While both measurements contribute to the overall surface area, they represent distinct aspects of the cylinder’s outer surface.
The curved surface area (CSA) refers to the area formed by the curved surface that connects the two circular bases of the cylinder. It does not include the area of the circular bases themselves. The curved surface area can be calculated using the formula CSA = 2πrh, where r is the radius of the circular base and h is the height of the cylinder.
On the other hand, the total surface area (TSA) includes the curved surface area as well as the areas of the two circular bases. It represents the complete outer surface area of the cylinder. The formula for calculating the total surface area of a cylinder is TSA = 2πrh + 2πr², where r is the radius of the circular base and h is the height of the cylinder.
In summary, the curved surface area only considers the area formed by the curved surface, while the total surface area takes into account the curved surface area along with the areas of the circular bases. Understanding these differences is crucial in accurately calculating and interpreting the surface area of a cylinder.
| Property | Total Surface Area (TSA) | Curved Surface Area (CSA) |
|---|---|---|
| Definition | The total area of all the surfaces of the cylinder, including the curved surface and the two circular bases. | The area of the curved surface of the cylinder, excluding the area of the circular bases. |
| Formula | TSA = 2πrh + 2πr² | CSA = 2πrh |
| Components | Includes the curved surface area and the areas of the two circular bases. | Includes only the curved surface area, excluding the areas of the circular bases. |
Understanding the differences between TSA and CSA provides valuable insights into the surface area of a cylinder and allows for more accurate calculations and interpretations.
Right and Oblique Cylinder
Cylinders can be classified into two main types: right cylinders and oblique cylinders. The classification is based on the orientation of the axis of the cylinder in relation to the circular bases.

Right Cylinder
A right cylinder is a cylinder in which the axis is perpendicular to the circular bases, forming a right angle. This means that the axis is perpendicular to the plane of each base, creating a shape that is perfectly upright. Right cylinders are the most common type of cylinder encountered in everyday life.
Oblique Cylinder
An oblique cylinder is a cylinder in which the axis is not perpendicular to the circular bases. This means that the axis does not form a right angle with the plane of the bases. As a result, the shape of an oblique cylinder appears tilted or slanted. Oblique cylinders are less common and are often encountered in more complex geometric structures.
When calculating the surface area of a cylinder, it is important to consider whether the cylinder is a right cylinder or an oblique cylinder. The formulas and calculations will differ depending on the orientation of the axis.
Surface Area of a Half Cylinder
A half cylinder is a cylinder that has been cut in half along its central axis. It consists of one circular base and a curved surface that extends from the base to the cut edge. Finding the surface area of a half cylinder requires calculating the area of the curved surface and the area of the circular base.
To calculate the surface area of a half cylinder, follow these steps:
Step 1: Identify the Dimensions
Measure the radius (r) of the circular base and the height (h) of the half cylinder.
Step 2: Calculate the Curved Surface Area
To calculate the curved surface area, use the formula for the curved surface area of a cylinder: CSA = 2πrh. Substitute the values of the radius (r) and height (h) into the formula and calculate the curved surface area.
Step 3: Calculate the Area of the Circular Base
To calculate the area of the circular base, use the formula for the area of a circle: A = πr². Substitute the value of the radius (r) into the formula and calculate the area of the circular base.
Step 4: Calculate the Total Surface Area
To calculate the total surface area, add the curved surface area calculated in step 2 to the area of the circular base calculated in step 3.
By following these steps, you can accurately determine the surface area of a half cylinder and obtain an accurate measurement of the area covered by its outer surface.
Derivation of Surface Area of a Cylinder
The derivation of the formula for the surface area of a cylinder involves breaking down the cylinder into its individual components and calculating the surface area of each component separately.
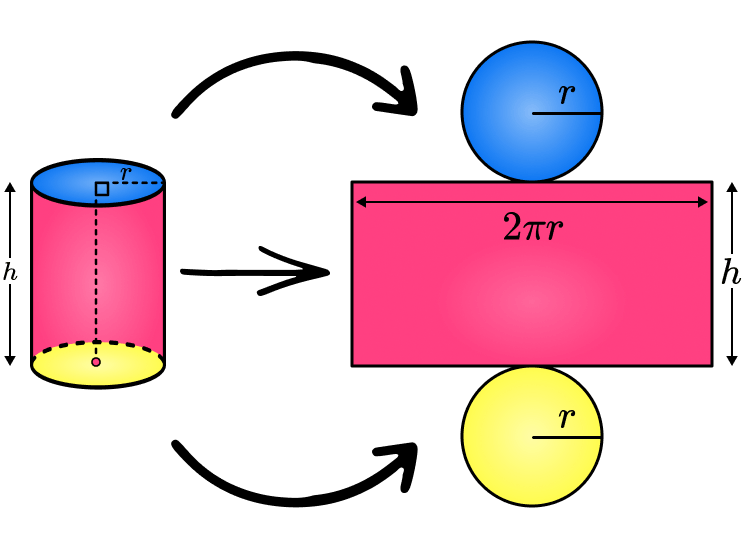
Consider a cylinder with a radius (r) and a height (h). The cylinder can be divided into three parts: two circular bases and a curved surface.
The area of each circular base can be calculated using the formula for the area of a circle: A = πr². Since there are two circular bases, the total area of the bases is 2πr².
The curved surface of the cylinder can be “unrolled” and transformed into a rectangle. The length of the rectangle is equal to the circumference of the circular base, which is 2πr. The width of the rectangle is equal to the height of the cylinder, which is h. Therefore, the area of the curved surface is 2πrh.
To find the total surface area of the cylinder, we sum the areas of the two circular bases and the area of the curved surface:
Total Surface Area = 2πr² + 2πrh
Simplifying the equation, we get:
Total Surface Area = 2πr(r + h)
This is the derived formula for the surface area of a cylinder.
The derivation of the surface area formula provides a deeper understanding of the components that contribute to the total surface area of a cylinder and how to calculate each component individually.
Properties of Surface Area of a Cylinder
The surface area of a cylinder possesses several important properties that contribute to its mathematical and real-world applications. These properties help us understand and manipulate the surface area of a cylinder in various contexts. Here are some key properties of the surface area of a cylinder:
1. Proportional to Height and Radius: The surface area of a cylinder is directly proportional to both the height and the radius. Increasing either the height or the radius will result in an increase in the surface area, while decreasing them will lead to a decrease in the surface area.
2. Doubling the Dimensions: If the dimensions of a cylinder are doubled, the surface area will be quadrupled. This is because the surface area of a cylinder is proportional to the square of the radius and the height.
3. Symmetry: The surface area of a cylinder exhibits symmetry. The areas of the two circular bases are equal, and the curved surface area is symmetrical about the axis of the cylinder.
4. Additivity: The surface area of a cylinder is additive. This means that the total surface area is the sum of the areas of the curved surface and the two circular bases.
5. Relationship to Volume: The surface area of a cylinder is not directly related to its volume. While the volume of a cylinder is a measure of the space enclosed by the shape, the surface area represents the area covered by the outer surface. The two concepts are distinct but related.
Understanding these properties of the surface area of a cylinder enables us to make accurate calculations and interpretations in various mathematical and real-world scenarios.
Volume of Cylinder
The volume of a cylinder refers to the amount of space enclosed by the shape. It is a measure of the total capacity or the total amount of material that can be contained within the cylinder. The volume is expressed in cubic units, such as cubic centimeters (cm³) or cubic meters (m³).
The formula for calculating the volume of a cylinder is given as:
Volume of Cylinder = πr²h
where:
- π (Pi) represents the mathematical constant approximately equal to 3.14159.
- r is the radius of the circular base of the cylinder.
- h is the height of the cylinder.
By calculating the volume of a cylinder, we can determine the amount of space it occupies or the amount of material it can hold. The volume is a crucial measurement in various mathematical and real-world applications.

Solved Examples on Surface Area of a Cylinder
To further illustrate the concepts and formulas discussed, let’s solve a few examples related to the surface area of a cylinder.
Example 1: Find the surface area of a cylinder with a radius of 5 cm and a height of 10 cm.
Solution: Given: Radius (r) = 5 cm Height (h) = 10 cm
Using the formula for the surface area of a cylinder: TSA = 2πrh + 2πr²
Substituting the given values: TSA = 2π(5)(10) + 2π(5)² TSA = 100π + 50π TSA = 150π cm² (Approximately 471 cm²)
Therefore, the surface area of the cylinder is approximately 150π cm² or 471 cm².
Example 2: A cylindrical pipe has a surface area of 250 cm². If the radius of the pipe is 3 cm, find the height of the pipe.
Solution: Given: Surface Area (TSA) = 250 cm² Radius (r) = 3 cm
Using the formula for the surface area of a cylinder: TSA = 2πrh + 2πr²
Substituting the given values: 250 = 2π(3)h + 2π(3)² 250 = 6πh + 18π 250 = 24πh h = 250 / (24π) h ≈ 3.31 cm
Therefore, the height of the pipe is approximately 3.31 cm.
By solving these examples, we can see how the formulas for the surface area of a cylinder are applied to real-world situations, allowing us to determine the surface area of different cylindrical objects.
How Kunduz Can Help You Learn How To Find The Surface Area of a Cylinder?
At Kunduz, we understand the importance of mastering mathematical concepts, including the calculation of the surface area of a cylinder. We are committed to providing comprehensive and accessible learning materials to assist students in their mathematical journey.
Whether you are a student looking to excel in your math classes or an educator seeking additional resources for your students, Kunduz is here to support you. Our dedicated team of experts is constantly updating and expanding our content to ensure the highest quality of education.
Join Kunduz today and unlock your mathematical potential. Let us guide you through the intricacies of the surface area of a cylinder and empower you to achieve your academic goals.
