In the realm of mathematics, there are various properties that help us establish relationships and draw conclusions. One such property is the transitive property, which allows us to make inferences based on established relationships between quantities. The transitive property is a fundamental concept in mathematics, particularly in algebra and geometry. It provides a logical framework for making deductions and proving mathematical statements.
For those exploring the visual representation of set relationships through transitive property and interested in diverse mathematical concepts, our hyperbolic functions and explicit formula pages serve as enriching references.
What is the Transitive Property?
The transitive property is a property by which if two quantities are related to a third quantity in the same manner, then the first two quantities are also related to each other in that manner. In simpler terms, if A is related to B and B is related to C, then we can conclude that A is related to C. This property allows us to establish a chain of relationships and make deductions based on those relationships.
The transitive property is often used to establish equality between quantities. If A is equal to B and B is equal to C, then we can safely say that A is equal to C. This property is not limited to equality; it can also be applied to inequalities, congruence, and other mathematical relationships.
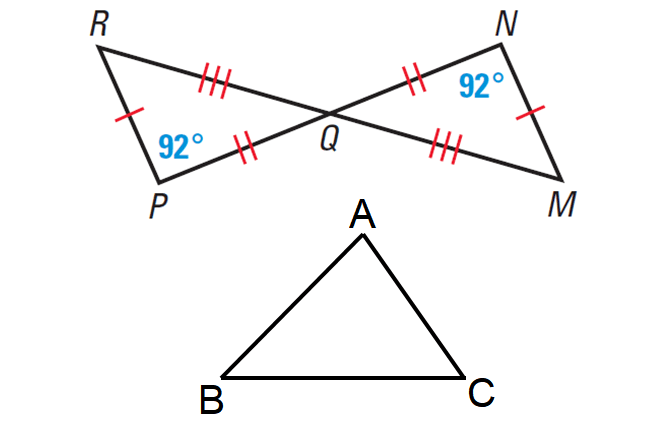
Transitive Property of Equality
The transitive property of equality states that if A is equal to B and B is equal to C, then A is equal to C. This property allows us to establish equality between quantities based on their relationships with a common third quantity. It is a fundamental concept in algebra, where it is used to solve equations and establish mathematical equivalences.
For example, suppose we have the equations A = B and B = C. By applying the transitive property of equality, we can conclude that A = C. This property allows us to simplify equations and make substitutions, making it a valuable tool in algebraic manipulations.
Transitive Property of Inequality
The transitive property also applies to inequalities. If A is less than B and B is less than C, then we can conclude that A is less than C. This property allows us to establish relationships between quantities based on their relative magnitudes. It is particularly useful in comparing numerical values and establishing order.
For example, let’s say we have the inequalities A < B and B < C. By applying the transitive property of inequality, we can deduce that A < C. This property helps us establish the order of quantities and make comparisons based on their relative sizes.
The transitive property of inequality can also be applied to other inequality symbols such as greater than, less than or equal to, and greater than or equal to. The underlying principle remains the same: if the relationship holds true between two quantities and the same relationship holds between those quantities and a third quantity, then the relationship also holds between the first and third quantities.
Transitive Property of Congruence
In geometry, the transitive property is used to establish congruence between geometric figures. If figure A is congruent to figure B and figure B is congruent to figure C, then we can conclude that figure A is congruent to figure C. This property allows us to establish congruence relationships between shapes and figures based on their relationships with a common third figure.
For example, let’s consider three triangles: triangle ABC, triangle PQR, and triangle XYZ. If triangle ABC is congruent to triangle PQR and triangle PQR is congruent to triangle XYZ, then we can apply the transitive property of congruence to conclude that triangle ABC is congruent to triangle XYZ. This property helps us establish equality between shapes and figures and make deductions based on their congruence relationships.
Transitive Property of Parallel Lines
The transitive property can also be applied to establish relationships between parallel lines. If line A is parallel to line B and line B is parallel to line C, then we can conclude that line A is parallel to line C. This property allows us to establish parallelism between lines based on their relationships with a common third line.
For example, if line A is parallel to line B and line B is parallel to line C, then we can apply the transitive property of parallel lines to conclude that line A is parallel to line C. This property helps us establish parallel relationships and make deductions based on the parallelism of lines.
Transitive Property Formula
The formula for the transitive property is simple and concise: if A is related to B and B is related to C, then A is related to C. This can be represented symbolically as A = B, B = C, then A = C. The transitive property formula provides a concise way to express the logical relationship between quantities.
When Do We Use Transitive Property?
The transitive property is used whenever we have established relationships between quantities and want to draw conclusions based on those relationships. It is particularly useful in algebra, geometry, and other branches of mathematics where relationships between quantities play a crucial role.
The transitive property is applied in various mathematical scenarios, such as solving equations, proving theorems, establishing congruence between figures, and comparing numerical values. It allows us to simplify expressions, make substitutions, establish equivalences, and draw logical conclusions based on established relationships.
How to Avoid Transitive Property Errors?
While the transitive property is a powerful tool in mathematics, it is important to use it correctly to avoid errors and misconceptions. Here are some tips to avoid common errors when applying the transitive property:
- Ensure that the relationship between quantities is consistent: The transitive property requires that the relationship between quantities remains the same throughout. If the relationship changes, the transitive property cannot be applied.
- Pay attention to the direction of inequality symbols: When using the transitive property of inequality, it is important to consider the direction of the inequality symbols. The transitive property holds true for the same direction of inequality (e.g., less than to less than), but not for opposite directions (e.g., less than to greater than).
- Be cautious with congruence relationships: When applying the transitive property of congruence, make sure that the congruence relationships between figures are established correctly. Mistakes in establishing congruence can lead to erroneous conclusions.
- Check for valid assumptions: The transitive property relies on valid assumptions and established relationships. Make sure that the assumptions and relationships are valid and consistent with the given information.
By following these guidelines, you can avoid common errors when applying the transitive property and ensure accurate and logical deductions in mathematical reasoning.
How to Use Transitive Property?
To use the transitive property, you need to have established relationships between quantities. Here is a step-by-step guide on how to use the transitive property effectively:
- Identify the relationships: Determine the relationships between the quantities or figures involved. This could be equality, inequality, congruence, or parallelism.
- Verify the consistency of relationships: Ensure that the relationships between quantities or figures are consistent throughout. If the relationships change, the transitive property cannot be applied.
- Apply the transitive property: If the relationships are consistent, apply the transitive property to establish relationships between the first and third quantities or figures. Use the transitive property formula: If A is related to B and B is related to C, then A is related to C.
- Draw conclusions: Based on the application of the transitive property, draw logical conclusions about the relationships between the quantities or figures involved.
By following these steps, you can effectively use the transitive property to establish relationships and draw conclusions based on those relationships.
Transitive Property of Order
The transitive property can also be applied to establish relationships between ordered quantities. If A is greater than B and B is greater than C, then we can conclude that A is greater than C. This property allows us to establish order relationships between quantities based on their relative magnitudes.
For example, suppose we have the inequalities A > B and B > C. By applying the transitive property of order, we can deduce that A > C. This property helps us establish the order of quantities and make comparisons based on their relative sizes.
The transitive property of order is particularly useful in establishing rankings, making comparisons, and organizing data in numerical or sequential order.
Solved Examples on Transitive Property
Let’s work through some examples to apply the transitive property and demonstrate its practical use in solving mathematical problems.
Example 1: Solve the equation x – 3 = 7, and use the transitive property to verify the solution.
Solution: Step 1: Start with the equation x – 3 = 7. Step 2: Add 3 to both sides of the equation to isolate x: x – 3 + 3 = 7 + 3. Step 3: Simplify: x = 10. Step 4: Now, let’s verify the solution using the transitive property. We know that x = 10, and we also know that 10 = 10 by the reflexive property of equality. By applying the transitive property, we can conclude that x = 10.
Therefore, the solution x = 10 is verified using the transitive property.
Example 2: Consider three angles, A, B, and C, such that A = 60°, B = 60°, and B = C. Use the transitive property to find the measure of angle C.
Solution: Given: A = 60°, B = 60°, and B = C. By the transitive property, we can conclude that A = C. Therefore, the measure of angle C is 60°.
By applying the transitive property, we can establish the equality between angles A and C based on their relationships with angle B.
How Kunduz Can Help You Learn Transitive Property?
At Kunduz, we understand the importance of a strong foundation in mathematics. Our comprehensive learning resources and expert instructors are dedicated to helping you master concepts like the transitive property. Whether you’re struggling with algebra, geometry, or any other branch of mathematics, we have the tools and support you need to succeed.
Our interactive lessons, practice problems, and step-by-step explanations ensure that you can grasp the transitive property and apply it confidently. Our experienced instructors are always available to answer your questions and provide personalized guidance.
Join Kunduz today and experience the power of personalized learning. Empower yourself with a deep understanding of mathematical concepts and excel in your academic journey. With Kunduz, learning math has never been easier or more enjoyable.
