A triangular pyramid is a fascinating three-dimensional shape that has attracted the attention of mathematicians and geometry enthusiasts for centuries. In this comprehensive guide, we will explore the definition, properties, types, area and volume formulas, as well as provide examples to help you gain a deeper understanding of this geometric solid.
An Introduction to Triangular Pyramids
Geometry is a branch of mathematics that deals with the properties and relationships of shapes and figures. Triangular pyramids, also known as tetrahedrons, are one of the fundamental shapes studied in geometry. They are three-dimensional solids with a triangular base and three triangular faces that meet at a common vertex.
Triangular pyramids can be found in various natural and man-made structures, such as the pyramids of Egypt, the Eiffel Tower, and even molecular structures. Understanding their properties and characteristics can help us analyze and comprehend the world around us.
What is a Triangular Pyramid?
A triangular pyramid is a geometric solid in which all of its faces are triangles. It consists of four triangular faces, six edges, and four vertices. The base of the pyramid is a triangle, and the other three faces are triangular, meeting at a single point called the apex.
Triangular pyramids can be further classified into regular and irregular pyramids. Regular triangular pyramids have equilateral triangles as their faces, while irregular triangular pyramids have triangles that are not equilateral. However, unless specified otherwise, triangular pyramids are generally assumed to be regular.

Triangular Pyramid Nets
Nets are two-dimensional representations of three-dimensional shapes that can be cut out and folded to form the actual solid. A triangular pyramid net is a pattern that forms when the surface of the triangular pyramid is laid flat. It consists of four triangles that represent the faces of the pyramid.
By examining the net of a triangular pyramid, we can better understand its structure and visualize how it folds to create the three-dimensional shape. This visualization is particularly useful when calculating the surface area of the pyramid.
To create a net of a triangular pyramid, take a sheet of paper and copy one of the two different nets shown below. Cut along the edges and fold the paper as shown in the picture to form a triangular pyramid.
Triangular Pyramid Formulas
To calculate the properties of a triangular pyramid, we can use various formulas. Let’s explore the formulas for finding the surface area and volume of a triangular pyramid.
Surface Area of Triangular Pyramid Formula
The surface area of a triangular pyramid is the sum of the areas of all its faces, including the base. The formula for calculating the surface area is given by:
Surface Area = Base Area + 0.5 × (Perimeter of Base × Slant Height)
The component representing the base area is straightforward, while the latter term calculates the total area of the three triangular faces.
How To Find The Surface Area of Triangular Pyramid
Step 1: Calculate the area of the triangular base using the appropriate formula based on the type of triangle (equilateral, isosceles, or scalene).
Step 2: Compute the perimeter of the base by adding the lengths of all its sides.
Step 3: Multiply the perimeter of the base by the slant height and divide the result by two. This gives the total area of the three triangular faces.
Step 4: Finally, add the base area and the area of the three faces to get the total surface area of the pyramid.
Volume of Triangular Pyramid Formula
The volume of a three-dimensional shape represents the amount of space it occupies. For a triangular pyramid, the volume can be calculated using the formula:
Volume = (1/3) × Base Area × Height
This formula denotes that the volume of a triangular pyramid is one-third the product of its base area and height.
How To Find The Volume of Triangular Pyramid
Step 1: Calculate the area of the triangular base using the appropriate formula.
Step 2: Multiply the base area by the height of the pyramid.
Step 3: Divide the product obtained in step 2 by three to find the volume.
Properties of Triangular Pyramid
Understanding the properties of a triangular pyramid can help us identify and classify this geometric solid. Here are some important properties to consider:
- A triangular pyramid has four triangular faces, six edges, and four vertices.
- At each vertex of the pyramid, three edges meet.
- Unlike other polyhedrons, a triangular pyramid does not have parallel faces.
- A regular triangular pyramid consists of equilateral triangles for all its faces. It also has six planes of symmetry.
- Triangular pyramids can be classified as regular, irregular, or right-angled, depending on the shape and orientation of the base triangle.
Types of Triangular Pyramids
Triangular pyramids can be further classified into different types based on their characteristics. Let’s explore the three main types of triangular pyramids:
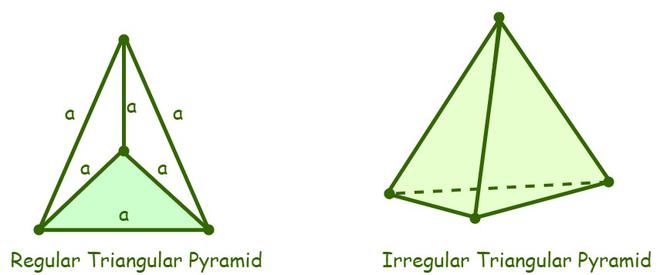
Regular Triangular Pyramid
A regular triangular pyramid is a type of pyramid where all the faces are equilateral triangles. In this pyramid, all internal angles measure 60 degrees. Regular triangular pyramids are symmetrical and have a pleasing aesthetic appearance.
Irregular Triangular Pyramid
An irregular triangular pyramid also consists of triangular faces, but they are not equilateral. The angles in each face of the pyramid add up to 180 degrees, as they are triangular. Unless specifically mentioned as irregular, triangular pyramids are generally assumed to be regular.
Right Triangular Pyramid
A right triangular pyramid has a base that is a right-angled triangle, with the apex aligned above the center of the base. It has one right-angled face, three triangular faces, six edges, and four vertices. Right triangular pyramids have specific applications in geometry and engineering.
Triangular Pyramid Faces, Edges, and Vertices
To gain a better understanding of a triangular pyramid’s structure, let’s explore its faces, edges, and vertices.
A triangular pyramid has four faces, all of which are triangles. The base of the pyramid is a triangle, and the other three faces are triangular, meeting at a single point called the apex.
The pyramid also has six edges, which are the line segments where the faces intersect. At each vertex, three edges meet, forming a vertex angle.
Lastly, a triangular pyramid has four vertices, which are the points where the edges intersect. Three vertices are located at the base of the pyramid, while the fourth vertex is at the apex.
Differences between Triangular Prism and Triangular Pyramid
Triangular prisms and triangular pyramids are both three-dimensional solids with triangular bases, but they have distinct differences. Let’s compare these two shapes side by side:
| Triangular Prism | Triangular Pyramid |
|---|---|
| Has two parallel triangular faces called bases | Has a single triangular base |
| Has three rectangular faces connecting the bases | Has three triangular faces connecting the base to the apex |
| Has five faces, nine edges, and six vertices | Has four faces, six edges, and four vertices |
| Volume formula: Base Area × Height | Volume formula: 1/3 × Base Area × Height |
While both shapes share a triangular base, the presence of additional faces in a triangular prism distinguishes it from a triangular pyramid. Triangular prisms have a more complex structure, while triangular pyramids have a simpler and more pointed shape.
Solved Examples on Triangular Pyramid
Let’s delve into some examples to further illustrate the concepts and formulas related to triangular pyramids.
Example 1: If two congruent triangular pyramids are stuck together along their base, they form a triangular bipyramid. How many faces, edges, and vertices does this bipyramid have?
Solution: The triangular bipyramid has 6 triangular faces, 9 edges, and 5 vertices.
Example 2: Find the volume of a regular triangular pyramid with a side length measuring 5 units. (Round off the answer to 2 decimal places)
Solution: Using the formula for the volume of a regular triangular pyramid, we have:
Volume = (5^3) / (6√2) = 125 / 8.485 ≈ 14.73 units^3
Therefore, the volume of the regular triangular pyramid is approximately 14.73 units^3.
Example 3: Each edge of a regular triangular pyramid is of length 6 units. Find its total surface area.
Solution: The total surface area of a regular triangular pyramid can be calculated using the formula:
TSA = √3 × a^2
Substituting the given edge length, we have:
TSA = √3 × 6^2 = √3 × 36 ≈ 62.35 units^2
Therefore, the total surface area of the regular triangular pyramid is approximately 62.35 units^2.
How Kunduz Can Help You Learn Triangular Pyramids?
At Kunduz, we understand the importance of a strong foundation in mathematics. Our comprehensive online math program offers interactive lessons, personalized tutoring, and a wealth of study materials to help students excel in geometry and other math topics.
Our experienced tutors provide step-by-step guidance and answering any questions students may have.
