Trigonometry is a branch of mathematics that focuses on the study of the relationship between angles and the sides of a right-angled triangle. It is a fundamental concept developed by the Greek mathematician Hipparchus and has since found extensive applications in various fields. In this article, we will explore the basics of trigonometry, including trigonometric functions, trigonometric ratios, trigonometric tables, formulas, and examples.
An Introduction to Trigonometry
Trigonometry is a vital branch of mathematics that plays a crucial role in many areas such as physics, engineering, and computer science. It deals with the measurement of angles and the relationships between the sides and angles of a right-angled triangle. By understanding these relationships, we can solve problems involving angles and distances.
What is Trigonometry?
Trigonometry is the study of the relationships between the sides and angles of triangles. It helps us find missing angles or sides of a right triangle using trigonometric functions, formulas, and identities. Trigonometry can be measured in degrees or radians, with commonly used angles such as 0°, 30°, 45°, 60°, and 90°. It is further classified into two sub-branches: plane trigonometry and spherical trigonometry.
Trigonometry Basics
To understand trigonometry, we need to familiarize ourselves with the basic concepts. In a right-angled triangle, we have three sides: the hypotenuse, the side opposite the right angle, and the adjacent side. The primary trigonometric functions are sine, cosine, and tangent, which are abbreviated as sin, cos, and tan, respectively. These functions are defined based on the ratios of the sides of a right triangle.
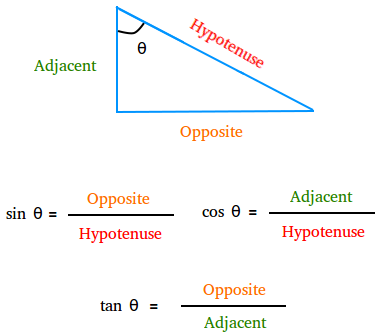
Trigonometry Ratios
Trigonometry ratios, also known as trigonometric functions, are the ratios of the sides of a right triangle with respect to its angles. There are six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent. These functions can be calculated using specific formulas based on the sides of the triangle. Here is a table that summarizes the trigonometric ratios:
| Function | Abbreviation | Relationship to sides of a right triangle |
|---|---|---|
| Sine | sin | Opposite side / Hypotenuse |
| Cosine | cos | Adjacent side / Hypotenuse |
| Tangent | tan | Opposite side / Adjacent side |
| Cosecant | csc | Hypotenuse / Opposite side |
| Secant | sec | Hypotenuse / Adjacent side |
| Cotangent | cot | Adjacent side / Opposite side |
Trigonometric Table
A trigonometric table is a valuable tool that provides the values of trigonometric ratios for specific angles. These tables allow us to quickly find the values of sine, cosine, tangent, cosecant, secant, and cotangent for common angles. By referring to the trigonometric table, we can solve many trigonometric problems involving these ratios.
Below is a table showing the values of trigonometric ratios for common angles:
| Angles | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| Sin θ | 0 | 1/2 | √2/2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | √2/2 | 1/2 | 0 |
| Tan θ | 0 | √3/3 | 1 | √3 | ∞ |
| Csc θ | ∞ | 2 | √2 | 2/√3 | 1 |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
These values can be used to solve trigonometric problems and find the unknown angles or sides of a right triangle.
Trigonometric Functions Graphs
Graphs are visual representations of functions that help us understand their behavior and characteristics. Trigonometric functions can be graphed to visualize their patterns and relationships. The graphs of sine and cosine functions are periodic, with a period of 2π. The graphs of tangent, cotangent, secant, and cosecant functions are not periodic.

List of Trigonometric Formulas
Trigonometry involves a variety of formulas that relate the trigonometric functions to each other and to the angles of a triangle. These formulas are essential for solving trigonometric problems and simplifying trigonometric expressions. Some important trigonometric formulas include:
- Pythagorean Identities:
- sin²θ + cos²θ = 1
- tan²θ + 1 = sec²θ
- cot²θ + 1 = csc²θ
- Sum and Difference Identities:
- sin(x + y) = sin x cos y + cos x sin y
- cos(x + y) = cos x cos y – sin x sin y
- tan(x + y) = (tan x + tan y) / (1 – tan x tan y)
- Double Angle Identities:
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ – sin²θ
- tan 2θ = 2 tan θ / (1 – tan²θ)
These formulas, along with others, allow us to simplify trigonometric expressions and solve trigonometric equations.
Unit Circle and Trigonometric Values
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. It is used to understand the values of trigonometric functions for any angle. By considering the coordinates of points on the unit circle, we can determine the values of sine, cosine, and tangent for various angles.
Trigonometric values on the unit circle are as follows:
- Sine θ = y-coordinate on the unit circle
- Cosine θ = x-coordinate on the unit circle
- Tangent θ = sine θ / cosine θ
These values help us determine the trigonometric ratios for angles beyond the common angles found in the trigonometric table.
Trigonometric Identities
Trigonometric identities are equations that are true for all values of the variables involved. These identities relate the trigonometric functions to each other and are useful for simplifying trigonometric expressions. Some important trigonometric identities include:
- Even and Odd Identities:
- sin(-θ) = -sinθ
- cos(-θ) = cosθ
- tan(-θ) = -tanθ
- sec(-θ) = secθ
- csc(-θ) = -cscθ
- cot(-θ) = -cotθ
- Reciprocal Identities:
- cscθ = 1/sinθ
- secθ = 1/cosθ
- cotθ = 1/tanθ
- Pythagorean Identities:
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = csc²θ
These identities are essential tools for solving trigonometric equations and simplifying trigonometric expressions.
Applications of Trigonometry
Trigonometry has numerous applications in various fields. It is used in physics, engineering, architecture, computer science, and many other disciplines. Some applications of trigonometry include:
- Calculating distances and angles in navigation and surveying.
- Determining the height of buildings or mountains using triangulation methods.
- Analyzing the motion of objects in physics, such as projectile motion.
- Understanding the behavior of waves and vibrations in acoustics and waves.
- Modeling and analyzing periodic phenomena, such as sound and light waves.
These are just a few examples of how trigonometry is applied in real-world scenarios. Its versatility makes it a valuable tool in many scientific and technical fields.
Solved Examples on Trigonometry
To better understand trigonometry, let’s consider a few solved examples:
Example 1: Find the values of sin 45°, cos 60°, and tan 60°.
Using the trigonometric table, we have:
- sin 45° = 1/√2
- cos 60° = 1/2
- tan 60° = √3
Example 2: A boy is standing near a tree and wonders about its height. If the boy is standing 10 miles away from the tree and the angle of elevation is 20°, what is the height of the tree?
Using the tangent function, we have:
tan θ = Height/Distance between object & tree So, Height = Distance * tan θ
If the distance is 10 miles and the angle of elevation is 20°, then
Height = 10 * tan(20°) = 10 * 0.36 = 3.6 miles
Hence, the height of the tree is 3.6 miles.
These examples demonstrate how trigonometric ratios can be used to find the values of specific angles.
How Kunduz Can Help You Learn Trigonometry?
Kunduz is a comprehensive online learning platform that offers a wide range of resources to help you learn trigonometry. With easy-to-understand lessons, interactive quizzes, and step-by-step tutorials, Kunduz provides a supportive learning environment for students of all levels. Whether you’re a beginner or looking to enhance your trigonometry skills, Kunduz has the tools and resources you need to succeed. Our experienced tutors are available to answer your questions and provide personalized guidance. With Kunduz, you can master trigonometry at your own pace and achieve academic success.
