Triangles are one of the most fundamental shapes in geometry, recognizable by their three sides and three vertices. A triangle’s properties are determined by the lengths of its sides and the measures of its angles. This article will delve into the different types of triangles, their properties, and practical examples.
What is a Triangle?
A triangle is a three-sided polygon, and it’s where two sides meet that we find a vertex, forming an interior angle. Every triangle has three sides, three vertices, and three interior angles. For instance, if a triangle has vertices A, B, and C, it’s represented as △ABC.
What are the Different Types of Triangles?
Triangles come in various types, each distinguished by their sides and angles. A triangle’s classification can be based on its sides (equilateral, isosceles, or scalene) or based on its angles (acute, right, or obtuse).
Properties of Triangles
Several fundamental properties are inherent to all triangles. Firstly, the sum of all the interior angles in a triangle is always 180°, known as the angle-sum property. Secondly, the length of any two sides of a triangle is always greater than the length of the third side, known as the triangle inequality property. Lastly, the longest side of a triangle is opposite its largest angle, and the shortest side is opposite the smallest angle.
Classifying Triangles
To better understand the variations of triangles, we can classify them based on their sides and their angles.
Types of Triangle Based on Sides
- Equilateral Triangle: All three sides are the same length.
- Isosceles Triangle: Two sides are of equal length.
- Scalene Triangle: No sides are of equal length.
Types of Triangles Based on Angles
- Acute Triangle: All three angles measure less than 90°.
- Right Triangle: One angle measures exactly 90°.
- Obtuse Triangle: One angle measures more than 90°.
Furthermore, triangles can also be classified according to a combination of their sides and angles, such as an isosceles right triangle (two sides equal, one angle is 90°), or an obtuse scalene triangle (no sides equal, one angle is more than 90°).
| Types of Triangle Based on Sides | Types of Triangles Based on Angles |
|---|---|
| Equilateral Triangle | Acute Triangle |
| Isosceles Triangle | Right Triangle |
| Scalene Triangle | Obtuse Triangle |
Now that we have an overview of the different types of triangles, let’s delve into each type’s properties and characteristics.
Types of Triangles Based on Sides
Equilateral Triangle
An equilateral triangle has all three sides of equal length, and each interior angle measures 60°.
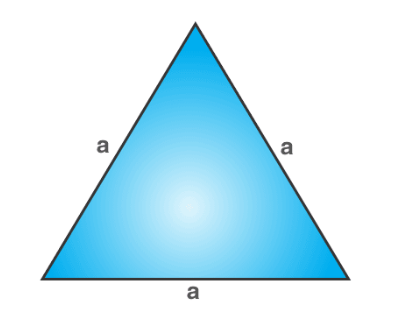
Properties of Equilateral Triangle
- All sides and angles are equal.
- Each angle measures 60°.
- It’s symmetrical along three lines of symmetry.
- It has rotational symmetry of order 3.
How to Find The Area of Equilateral Triangle
The formula to calculate the area of an equilateral triangle is Area = √3/4 * side².
How to Find The Perimeter of Equilateral Triangle
The perimeter of an equilateral triangle is simply three times the length of one side, or Perimeter = 3 * side.
Isosceles Triangle
An isosceles triangle has two sides of equal length. The two angles opposite these equal sides are also equal.
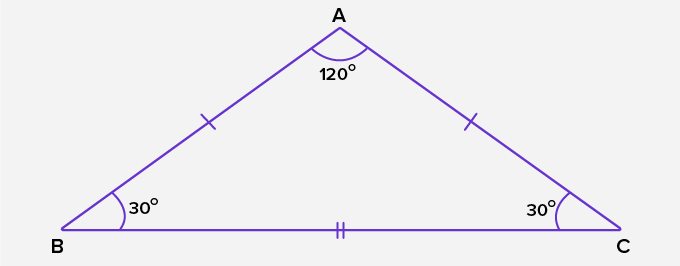
Properties of Isosceles Triangle
- Two sides and two angles are equal.
- It has one line of symmetry.
- It may have rotational symmetry of order 2.
How to Find The Area of Isosceles Triangle
The formula for the area of an isosceles triangle is Area = 1/2 * base * height.
How to Find The Perimeter of Isosceles Triangle
The perimeter of an isosceles triangle is the sum of the lengths of the three sides, or Perimeter = 2 * side + base.
Scalene Triangle
A scalene triangle has all sides and all interior angles of different measures.
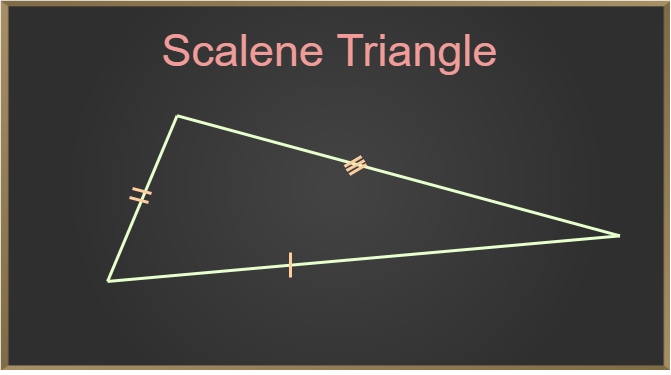
Properties of Scalene Triangle
- No sides and no angles are equal.
- It has no lines of symmetry.
- It has no rotational symmetry.
How to Find The Area of Scalene Triangle
The area of a scalene triangle can be found using Heron’s formula: Area = √[s(s - a)(s - b)(s - c)], where s is the semi-perimeter of the triangle, calculated as (a+b+c)/2, and a, b, c are the lengths of the sides.
How to Find The Perimeter of Scalene Triangle
The perimeter of a scalene triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Types of Triangles Based on Angles
Acute Triangle
An acute triangle has all interior angles less than 90°.
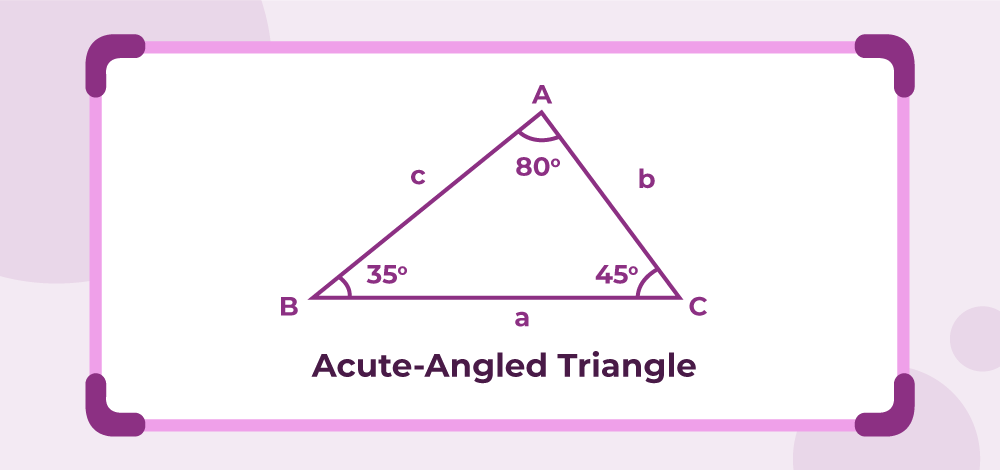
Properties of Acute Triangle
- All angles are acute (less than 90°).
- The sum of any two side lengths is greater than the length of the third side.
- The square of the length of the longest side is less than the sum of the squares of the lengths of the other two sides.
How to Find The Area of Acute Triangle
The area of an acute triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Acute Triangle
The perimeter of an acute triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Right Triangle
A right triangle has one angle that measures exactly 90°.

Properties of Right Triangle
- One angle measures 90°.
- The side opposite the right angle is the hypotenuse, and it’s the longest side.
- The other two sides are the legs of the triangle.
- The square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides (Pythagorean theorem).
How to Find The Area of Right Triangle
The area of a right triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Right Triangle
The perimeter of a right triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Obtuse Triangle
An obtuse triangle has one interior angle greater than 90°.
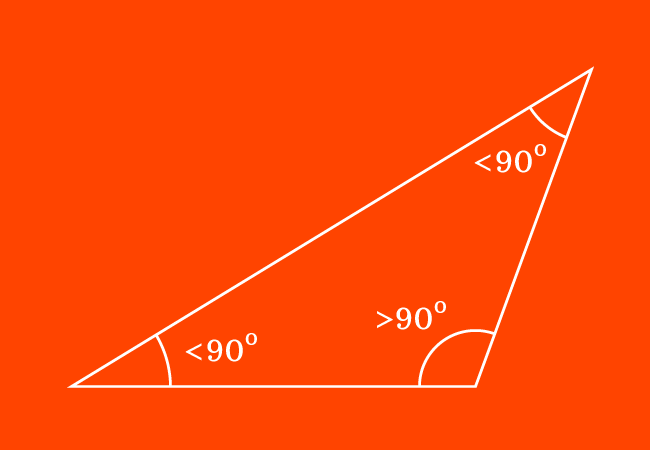
Properties of Obtuse Triangle
- One angle is obtuse (greater than 90°).
- The side opposite the obtuse angle is the longest side.
- The square of the length of the longest side is greater than the sum of the squares of the lengths of the other two sides.
How to Find The Area of Obtuse Triangle
The area of an obtuse triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Obtuse Triangle
The perimeter of an obtuse triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Types of Triangle Based on Sides and Angles
In addition to the classifications above, triangles can be further classified based on a combination of their sides and angles.
Equilateral or Equiangular Triangle
An equilateral or equiangular triangle has all sides and angles equal.
Properties of Equilateral or Equiangular Triangle
- All sides and angles are equal.
- Each angle measures 60°.
- It’s symmetrical along three lines of symmetry.
- It has rotational symmetry of order 3.
How to Find The Area of Equilateral or Equiangular Triangle
The formula to calculate the area of an equilateral or equiangular triangle is Area = √3/4 * side².
How to Find The Perimeter of Equilateral or Equiangular Triangle
The perimeter of an equilateral or equiangular triangle is simply three times the length of one side, or Perimeter = 3 * side.
Isosceles Right Triangle
An isosceles right triangle has two sides of equal length and one angle of 90°.
Properties of Isosceles Right Triangle
- Two sides and one angle are equal.
- One angle measures 90°.
- The hypotenuse is √2 times the length of each leg.
How to Find The Area of Isosceles Right Triangle
The area of an isosceles right triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Isosceles Right Triangle
The perimeter of an isosceles right triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Obtuse Isosceles Triangle
An obtuse isosceles triangle has two sides of equal length and one angle greater than 90°.
Properties of Obtuse Isosceles Triangle
- Two sides and two angles are equal.
- One angle is obtuse (greater than 90°).
How to Find The Area of Obtuse Isosceles Triangle
The area of an obtuse isosceles triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Obtuse Isosceles Triangle
The perimeter of an obtuse isosceles triangle is the sum of the lengths of its three sides, or Perimeter = 2 * side + base.
Acute Isosceles Triangle
An acute isosceles triangle has two sides of equal length and all angles less than 90°.
Properties of Acute Isosceles Triangle
- Two sides and two angles are equal.
- All angles are acute (less than 90°).
How to Find The Area of Acute Isosceles Triangle
The area of an acute isosceles triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Acute Isosceles Triangle
The perimeter of an acute isosceles triangle is the sum of the lengths of its three sides, or Perimeter = 2 * side + base.
Right Scalene Triangle
A right scalene triangle has no equal sides and one angle of 90°.
Properties of Right Scalene Triangle
- No sides are equal.
- One angle measures 90°.
- The side opposite the right angle is the hypotenuse, and it’s the longest side.
How to Find The Area of Right Scalene Triangle
The area of a right scalene triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Right Scalene Triangle
The perimeter of a right scalene triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Obtuse Scalene Triangle
An obtuse scalene triangle has no equal sides and one angle greater than 90°.
Properties of Obtuse Scalene Triangle
- No sides are equal.
- One angle is obtuse (greater than 90°).
How to Find The Area of Obtuse Scalene Triangle
The area of an obtuse scalene triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Obtuse Scalene Triangle
The perimeter of an obtuse scalene triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Acute Scalene Triangle
An acute scalene triangle has no equal sides, and all angles are less than 90°.
Properties of Acute Scalene Triangle
- No sides are equal.
- All angles are acute (less than 90°).
How to Find The Area of Acute Scalene Triangle
The area of an acute scalene triangle can be calculated using the formula Area = 1/2 * base * height.
How to Find The Perimeter of Acute Scalene Triangle
The perimeter of an acute scalene triangle is the sum of the lengths of its three sides, or Perimeter = a + b + c.
Parts of a Triangle
Each triangle consists of sides, vertices, and angles. The sides are the straight lines that form the triangle, the vertices are the points where the sides meet, and the angles are the spaces between the sides.
Triangles and Pythagorean Theorem
The Pythagorean theorem is a fundamental principle in geometry, and it applies to right-angled triangles. The theorem states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is key in calculating distances and lengths in various fields, including architecture, construction, navigation, and more.
Triangles and Euclidean Theorem
The Euclidean theorem is another crucial principle in geometry that extends the Pythagorean theorem. It states that the square of a line segment is equal to the sum of the squares of its projections on the coordinate axes. This theorem is commonly used in computer graphics, physics, and other areas that involve calculating distances and angles.
Area of a Triangle
The area of a triangle is a measure of the total space enclosed by the triangle. It’s calculated by multiplying the base of the triangle by its height and then dividing by two, Area = 1/2 * base * height. The base can be any side, and the height is the perpendicular line from the base to the opposite vertex.
Perimeter of Triangle
The perimeter of a triangle is calculated by adding the lengths of all its sides. Regardless of the type of triangle, the formula remains the same: Perimeter = a + b + c.
Solved Examples on Types of Triangles
Let’s go through a couple of examples to better understand the different types of triangles and how to calculate their properties.
Example 1: Classify the triangle as equilateral, isosceles, or scalene.
Solution: If all sides of a triangle are of different lengths, then it’s a scalene triangle.
Example 2: Classify the triangle as acute, right, or obtuse.
Solution: If all the interior angles of a triangle are less than 90°, then it’s an acute triangle.
Example 3: In an isosceles triangle, ABC, ∠A = 100° and ∠B = ∠C. Find the measure of ∠C.
Solution: According to the angle sum property of a triangle, ∠A + ∠B + ∠C = 180°. So, ∠B + ∠C = 180° – 100° = 80°. Since ∠B = ∠C, measure of ∠C = 80° ÷ 2 = 40°.
How Kunduz Can Help You Learn Types of Triangles?
Understanding the types of triangles and their properties is crucial in geometry. Kunduz offers an engaging and interactive platform to learn and master the concepts of triangles and many other topics. The platform provides detailed solutions and explanations to help you grasp the concepts effectively and apply them in solving problems.
Remember, the more you practice, the better you get at understanding and applying the concepts. Happy learning!
