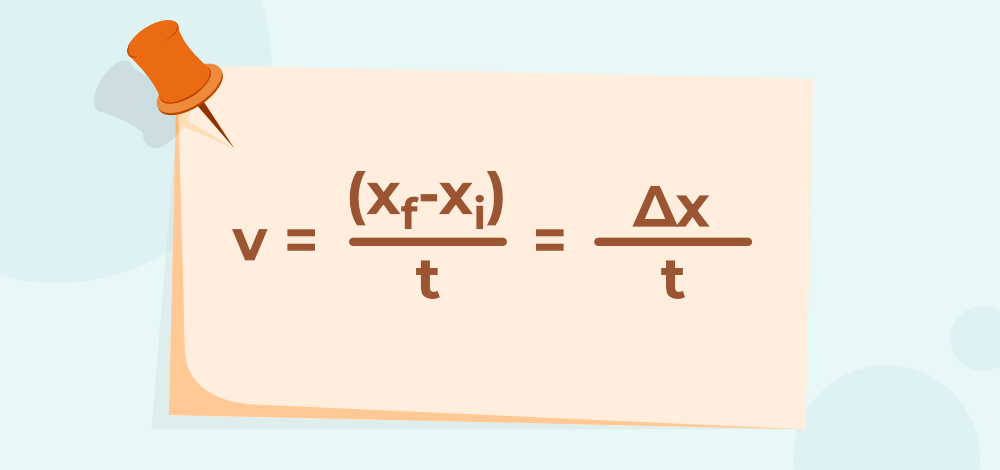Before diving into the depths of this fascinating concept, it’s important to grasp its most fundamental aspects. Velocity, a term often used interchangeably with speed, is a significant concept in the realm of physics. It serves as a measure of the rate and direction of an object’s motion.
You may already have an intuitive understanding of what velocity represents. For example, an object with a large displacement in a short amount of time is often associated with a high velocity. However, it’s essential to understand that velocity isn’t merely about how fast an object moves. It also encompasses the direction of the motion, making it a vector quantity. Velocity, therefore, carries two vital pieces of information: magnitude (how fast?) and direction (which way?).
What is Velocity?
The formal definition of velocity is the rate of change of an object’s position with respect to time. It can also be described as the speed at which an object moves in a specific direction. For example, if a car is moving at 60 kilometers per hour towards the north, that is the car’s velocity. The car’s speed, 60 kilometers per hour, is the magnitude, and the direction, north, completes the definition of velocity.
Velocity Formula
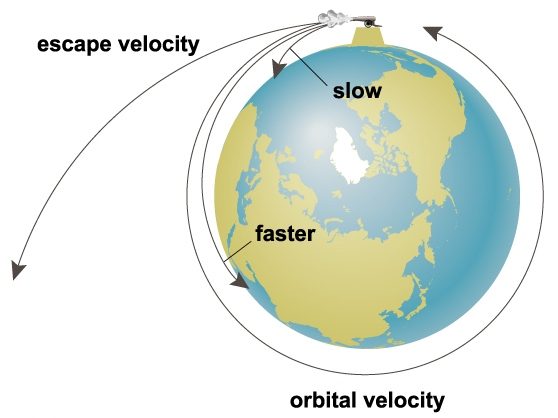
The most basic velocity formula is derived from its definition. It’s given by displacement (change in position) divided by time:
v = Δx / Δt
Here, ‘v’ represents velocity, ‘Δx’ denotes displacement, and ‘Δt’ signifies the time interval. Note that this formula gives the average velocity over the time interval ‘Δt’.
Velocity Equation
The velocity equation becomes more complex when we consider acceleration. If an object starts from an initial velocity ‘u’, and then accelerates at a rate ‘a’ for a time ‘t’, the final velocity ‘v’ can be calculated as:
v = u + at
This equation, known as the first equation of motion, allows us to calculate the final velocity of an object given its initial velocity, acceleration, and time.
For enthusiasts delving into the intricacies of velocity and its dynamics, our acceleration page serves as an essential companion, providing a deeper exploration into the fundamental relationship between velocity and acceleration, fostering a comprehensive understanding of motion and its mathematical representations.
How To Find Velocity?
To find velocity, you need to know the object’s displacement and the time it took for this displacement to occur. The steps are straightforward:
Step 1: Determine the displacement, which is the final position minus the initial position (Δx = xf – xi).
Step 2: Determine the time interval during which this displacement occurred (Δt).
Step 3: Plug these values into the velocity formula to find the average velocity.
Initial and Final Velocity
The terms ‘initial velocity’ and ‘final velocity’ refer to the velocities of an object at the start and end of a time interval, respectively. When an object begins to move, it starts with an initial velocity. As it continues to move, its velocity may change due to acceleration. The velocity it attains at the end of the motion is termed as the final velocity.
How to Find the Final Velocity?
To find the final velocity, you first need to determine the object’s initial velocity, acceleration, and time for which the motion occurred. The formula is given by:
v = u + at
Here, ‘v’ is the final velocity, ‘u’ is the initial velocity, ‘a’ is the acceleration, and ‘t’ is the time taken.
Types of Velocity
Velocity can be classified into various types depending on the nature of the motion. Some of the key types of velocity include:
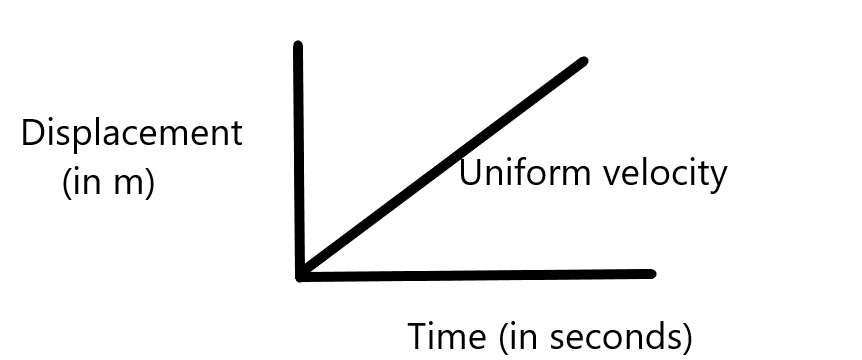
Uniform Velocity
Uniform velocity refers to the motion of an object in a straight line at a constant speed. In other words, the object covers equal displacements in equal time intervals.
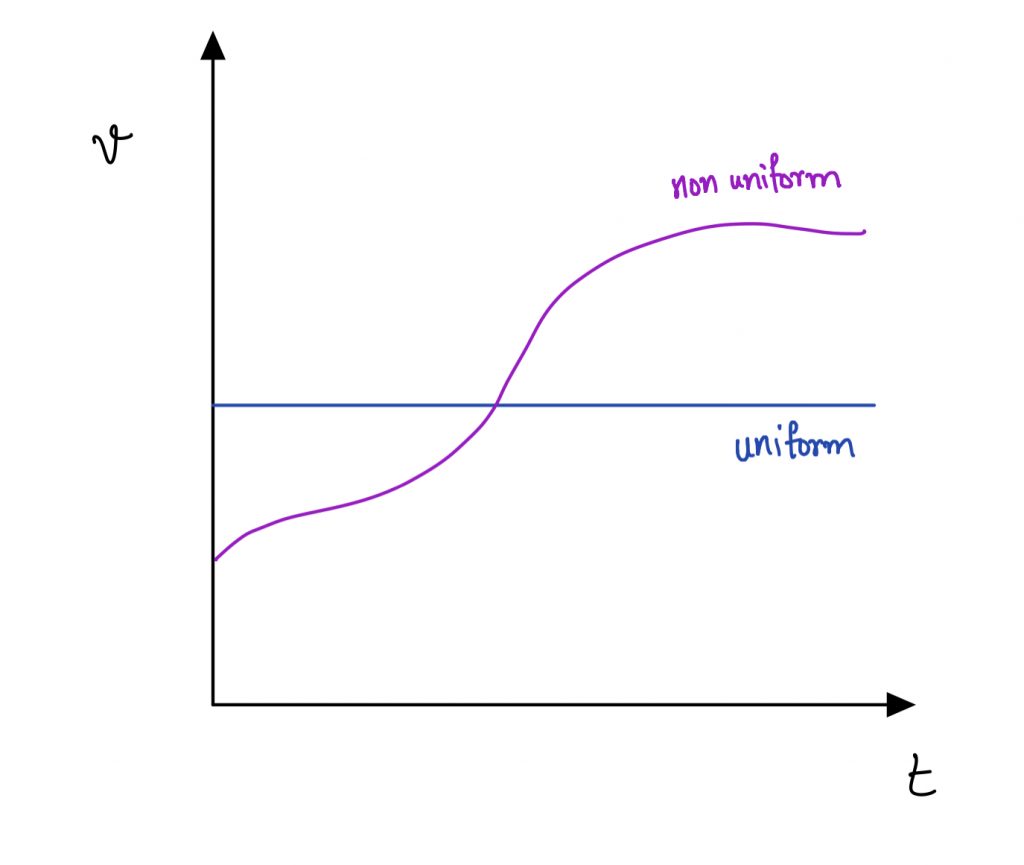
Non-Uniform Velocity
Non-uniform velocity occurs when an object covers unequal displacements in equal time intervals. This happens when an object’s speed, direction, or both change over time.
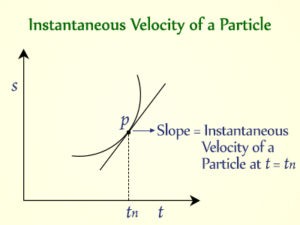
Instantaneous Velocity
Instantaneous velocity refers to the velocity of an object at a specific instant in time. It’s derived by considering an infinitesimally small time interval.
Average Velocity
Average velocity is calculated as the total displacement of an object divided by the total time it took for that displacement. It provides the overall rate of change in position for the entire motion.
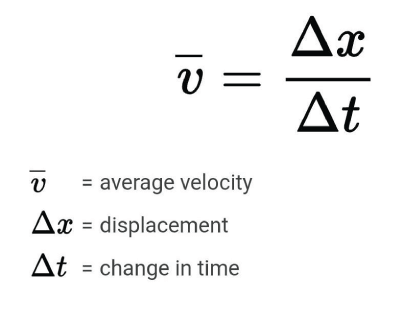
Constant Velocity
When an object moves in a straight line at a constant speed, it’s said to have a constant velocity. It implies that the object doesn’t accelerate or decelerate; its speed and direction remain unchanged throughout the motion.
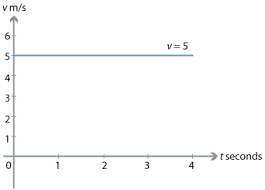
Angular Velocity
Angular velocity is a measure of the rate of change of angular displacement and is particularly relevant for objects moving along a circular path. The formula for angular velocity is:
ω = θ / t
where ‘ω’ is the angular velocity, ‘θ’ is the angular displacement, and ‘t’ is the time taken.
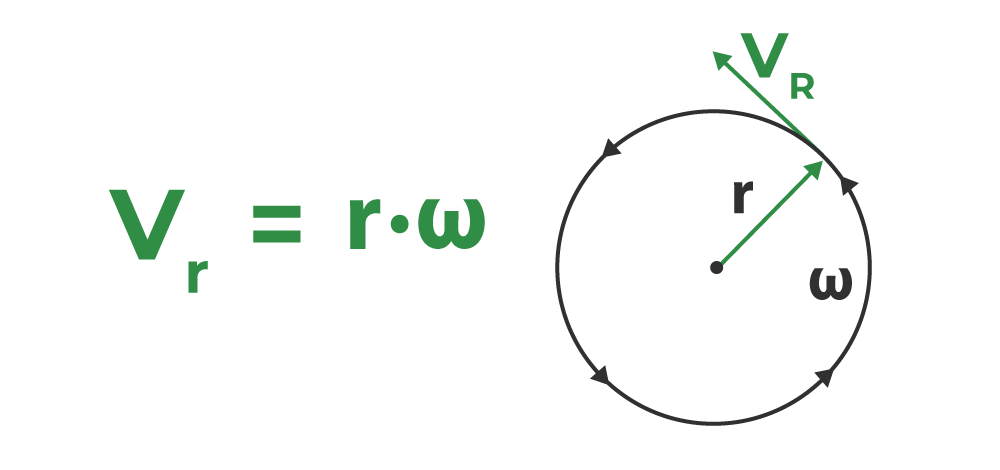
Escape Velocity
Escape velocity is the minimum velocity an object must have to escape the gravitational pull of a planet or other body. The formula for escape velocity is:
ve = √(2GM/r)
where ‘ve’ is the escape velocity, ‘G’ is the universal gravitational constant, ‘M’ is the mass of the body to be escaped from, and ‘r’ is the distance from the center of the mass.
SI Unit of Velocity
The standard unit of velocity in the International System of Units (SI) is meters per second (m/s). However, velocity can also be expressed in other units such as kilometers per hour (km/h), miles per hour (mph), or feet per second (ft/s) depending on the context.
Velocity Units
The velocity units are derived based on the formula of velocity. Since it’s a ratio of displacement (a length) to time, any length unit divided by any time unit can serve as a unit for velocity. The most commonly used units are meters per second (m/s), kilometers per hour (km/h), and miles per hour (mph).
Speed and Velocity
Speed is a scalar quantity that refers to “how fast an object is moving.” Velocity, on the other hand, is a vector quantity that accounts for both the object’s speed and its direction of motion. Therefore, while speed can never be negative, velocity can, depending on the direction of motion.
Solved Examples of Velocity
To better understand the concept of velocity, let’s work through a few examples:
- Suppose a cyclist covers a distance of 15 km to the east in 30 minutes. The velocity would be calculated as: Displacement (Δx) = 15 km = 15,000 m (convert km to m) Time (Δt) = 30 min = 1800 s (convert min to s) Velocity (v) = Δx / Δt = 15,000 m / 1800 s = 8.33 m/s (to the east)
- A bird flies south at a constant speed of 20 m/s for 10 seconds. The velocity would be: Velocity (v) = Displacement (Δx) / Time (Δt) = (20 m/s x 10 s) / 10 s = 20 m/s (south)
Difference between Speed and Velocity
The main difference between speed and velocity involves direction. Speed is a scalar quantity and only refers to the magnitude of motion. Velocity, being a vector quantity, considers both magnitude and direction. Therefore, two objects moving at the same speed can have different velocities if they’re moving in different directions.
| Aspect | Speed | Velocity |
|---|---|---|
| Definition | Speed is a scalar quantity that refers to how fast an object is moving. | Velocity is a vector quantity that refers to the rate at which an object changes its position. |
| Scalar/Vector | Scalar (only magnitude) | Vector (magnitude and direction) |
| Measurement | Measures how fast an object travels without considering its direction of travel. | Measures the rate of change of position of an object in a specific direction. |
| Formula | Speed = Distance / Time | Velocity = Displacement / Time |
| Units | Common units are meters per second (m/s), kilometers per hour (km/h), miles per hour (mph). | Same as speed, but direction is also specified. |
| Path Dependent | Yes, speed is path dependent. It does not consider the direction, just the total distance covered. | No, velocity is not path dependent. It is concerned with the shortest path between two points (displacement). |
| Zero Value | Speed can never be negative; the smallest value is zero, indicating no movement. | Velocity can be zero if there is no displacement; it can also be negative, indicating a change in direction. |
| Example | If a car travels 100 km in 2 hours, its speed is 50 km/h. | If a car moves 100 km east in 2 hours, its velocity is 50 km/h east. |
| Graph Representation | Represented by a speed-time graph, which shows speed on the y-axis and time on the x-axis. | Represented by a velocity-time graph, which can have both positive and negative values on the y-axis. |
| Instantaneous Measure | Instantaneous speed is the speed of an object at a particular moment in time. | Instantaneous velocity is the velocity of an object at a particular instant, considering its direction. |
| Changes with Direction | Speed does not change if the object changes direction. | Velocity changes if there is a change in the direction of the object’s motion. |
Why does Velocity Matter?
Understanding velocity is fundamental in physics and engineering as it relates to how objects move. It helps in predicting the future position of moving objects and is crucial for safety in transportation. Furthermore, the concept of velocity is foundational in the study of mechanics and is used in a wide range of practical applications such as vehicle design, flight navigation, athletic training, and even animation in video games and films.
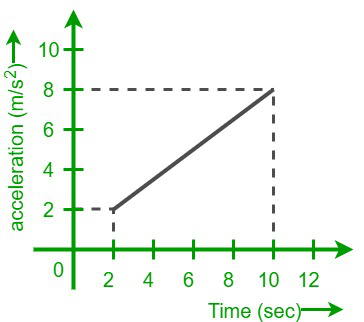
Calculating Average Velocity from an Acceleration-Time Graph
Acceleration-time graphs can be used to calculate average velocity. The area under the graph gives the change in velocity, and this can be divided by the total time to get the average velocity.
Can Velocity be Negative?
Yes, velocity can be negative. Negative velocity implies that the object is moving in the opposite direction to the direction defined as positive. Negative velocity does not mean the object is slowing down; it merely means it’s moving in the reverse direction.
In conclusion, velocity is a fundamental concept in physics that describes the rate of change of an object’s position. By understanding velocity, we can predict an object’s future location, which is vital in many fields such as engineering, transportation, sports, and more. Understanding the difference between speed and velocity, as well as the different types of velocity, can help us better understand the world around us.