The world of geometry is filled with various fascinating concepts, and one of them is vertical angles. This term represents a specific situation that arises when two lines intersect, creating pairs of equal angles. We refer to these as vertical or ‘vertically opposite’ angles. Understanding this concept forms a crucial part of mastering geometry, and our goal here is to facilitate that process.
What are the Vertical Angles?
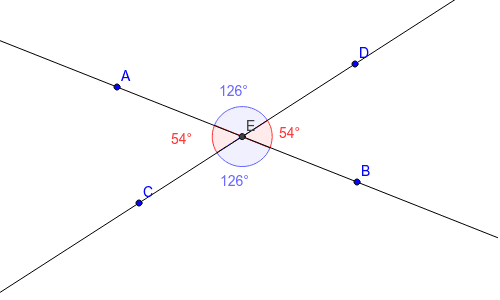
Vertical angles, sometimes referred to as vertically opposite angles, are the pairs of angles formed when two lines intersect each other. These angles are always directly across from each other and share a common vertex. However, they do not share any sides. The beauty of vertical angles lies in their inherent property: they are always congruent, meaning they have the same measure.
To provide an illustration, imagine an hourglass or the letter ‘X.’ The angles formed at the intersection point of the lines are vertical angles.
How To Find Vertical Angles?
Identifying vertical angles is a simple process once you know what to look for. Whenever you see two lines intersect, the angles formed directly across from each other at the intersection point are the vertical angles.
Remember, vertical angles are always equal. Thus, if you know the measure of one angle, you immediately know the measure of its vertical counterpart. This property comes in handy when solving various geometry problems, especially those involving intersecting lines.
Vertical Angles Characteristics
Vertical angles have some unique characteristics that set them apart and make them a fascinating topic in geometry. Here are some essential features of vertical angles:
- Congruency: Vertical angles are always congruent. This means that they have the same angle measure, irrespective of the length or direction of the intersecting lines.
- Non-adjacency: Vertical angles share the same vertex, but they do not share any sides or arms. This differentiates them from adjacent angles, which share both a vertex and a side.
- Supplementary angles: Vertical angles can be supplementary, but only in the case where the intersecting lines are perpendicular, i.e., they meet at a right angle.
It’s crucial to understand these characteristics as they form the basis of the vertical angles theorem and play a significant role in solving related geometry problems.
How To Solve Vertical Angles
While there is no direct formula for calculating vertical angles, understanding their properties can help solve related problems. Given two intersecting lines, you only need a single angle measure to determine the remaining three. This is because the other angle that is vertically opposite to the known angle will have the same measure, and the other two angles, which are supplementary to the known angle, will add up to 180 degrees.
How To Find the Measure of Vertical Angles?
The process of finding the measure of vertical angles relies on their inherent property of congruency. If the measure of one angle is given, its vertically opposite angle will have the same measure.
However, if the angle adjacent to the required vertical angle is provided, you can use the property of supplementary angles to find the measure. Subtract the given angle’s measure from 180 degrees, and you will get the measure of the vertical angle, as vertical angles and their adjacent angles are supplementary.
Using Vertical Angles to Find the Measurement of a Missing Angle
Vertical angles provide us with a powerful tool to find missing angle measures in geometry problems. Since vertical angles are always equal, if we are given the measure of one angle at an intersection, we can immediately determine the measure of the angle opposite to it.
Moreover, knowing that vertical angles and their adjacent angles add up to 180 degrees, we can also find the measure of the adjacent angles. This ability to ascertain the measure of missing angles makes understanding vertical angles a vital part of mastering geometry.
Properties of Vertical Angles
Vertical angles have some key properties that are essential to understanding and using them effectively. Here are the fundamental properties of vertical angles:
- Equal Measures: Vertical angles are always congruent, which means they have the same measure.
- Shared Vertex: Vertical angles share a common vertex, the point where the lines intersect.
- Supplementary Adjacent Angles: An angle adjacent to a vertical angle and the vertical angle itself are supplementary, adding up to 180 degrees.
- Non-adjacency: Vertical angles are never adjacent; they always lie opposite each other.
These properties make vertical angles a powerful concept in geometry, enabling us to solve various complex problems.
Vertical Angles Theorem and Proof
The Vertical Angles Theorem is a fundamental theorem in geometry that states, “Vertical angles are always congruent.” In other words, the angles opposite each other when two lines intersect are always equal.
The proof of this theorem is quite simple and is based on the concept of supplementary angles. We know that angles on a straight line add up to 180 degrees. So, if two angles form a linear pair, their measures add up to 180 degrees. Using this concept and the properties of equality, we can show that vertical angles are equal.

Facts About Vertical Angles
Now that we’ve covered the basics of vertical angles and the vertical angles theorem, let’s go over some interesting facts related to this topic:
- Same Measure: No matter the orientation or length of the intersecting lines, vertical angles always have the same measure.
- Not Necessarily Upright: The term “vertical” in vertical angles refers to their position directly across from each other at the intersection point, not their direction.
- Not Adjacent: Vertical angles are always opposite each other and are therefore never adjacent.
- Can Be Supplementary: Vertical angles can be supplementary, but this only occurs when the intersecting lines are perpendicular.
Understanding these facts can provide additional insight into the nature of vertical angles and their role in geometry.
Intersecting Chord Theorem of Angles
In the realm of circle geometry, vertical angles also play a significant role. The Intersecting Chord Theorem states that when two chords of a circle intersect inside the circle, two pairs of vertical angles are formed. The measure of the angle formed is half the sum of the arcs subtended by the vertical angles formed by the chords of the circle. This theorem showcases the importance of vertical angles beyond basic geometry and into the more complex world of circular geometry.
Frequently Asked Questions About Vertical Angles
Several common questions arise when studying vertical angles. Here are a few, along with their answers:
Why Are Vertical Angles Congruent?
Vertical angles are congruent due to their position. They are formed by the intersection of two lines, creating opposite angles with equal measures. This geometric property is a result of the angles sharing a common vertex and being on opposite sides of the intersecting lines, leading to their equal measures.
Are Vertical Angles Adjacent?
No, vertical angles are not adjacent. Adjacent angles share a common side, while vertical angles only share a vertex.
Are Vertical Angles Supplementary?
Vertical angles can be supplementary, but only in the case where the intersecting lines are perpendicular.
Are Vertical Angles Complementary?
Vertical angles are only complementary when each angle measures 45 degrees.
Can Vertical Angles Be Right Angles?
Yes, if the intersecting lines are perpendicular, forming a 90-degree angle, then the vertical angles are right angles.
Solved Examples on How to Use the Vertical Angles
To help solidify your understanding of vertical angles, let’s go through some examples:
Example 1: Given intersecting lines with an angle of 45 degrees, find the measure of the vertical and adjacent angles.
The vertical angle will also be 45 degrees (since vertical angles are congruent), and the adjacent angle will be 180 – 45 = 135 degrees (since vertical angles and their adjacent angles are supplementary).
Example 2: If one angle at an intersection of two lines is 70 degrees, find the measures of all the other angles.
The angle opposite to the given angle is also 70 degrees (vertical angles are equal). The other two angles are each 180 – 70 = 110 degrees (since vertical angles and their adjacent angles are supplementary).
Example 3: Two lines intersect, forming an angle of 120 degrees. Find the measure of the vertical and adjacent angles.
The vertical angle will also be 120 degrees, and the adjacent angle will be 180 – 120 = 60 degrees.
These examples demonstrate how to use the properties of vertical angles to solve problems in geometry.
How Kunduz Can Help You Learn Vertical Angles?
Understanding vertical angles and their properties is a crucial part of learning geometry, and Kunduz is here to help. With a wide range of resources and expert guidance, Kunduz provides a comprehensive learning platform that can significantly enhance your understanding of vertical angles and many other topics in mathematics.
Whether you’re struggling with a complex problem or just need to clarify a concept, Kunduz is your go-to resource for all your learning needs.

