Viscosity is a fundamental property of fluids that measures their resistance to flow. It is a measure of the internal friction between the layers of a fluid as they slide past each other during flow. In this article, we will explore the concept of viscosity, its importance, different types of viscosity, the formula to calculate viscosity, and real-life examples to illustrate its practical applications.
An Introduction to Viscosity of Water
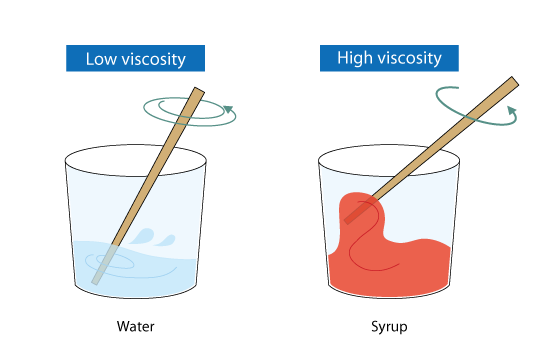
Water is a commonly known liquid with relatively low viscosity. It flows easily and quickly due to its low resistance to motion. This is because the intermolecular forces in water are weak, allowing the molecules to slide past each other with ease. As a result, water has a low viscosity compared to other liquids like honey or motor oil.
What is Viscosity?
Viscosity can be defined as the measurement of a fluid’s resistance to flow. It is a property that determines how easily or difficultly a fluid can flow under the action of an external force, such as gravity. The SI unit for measuring viscosity is Poiseiulle (PI), but it can also be expressed in other units such as Newton-Second per Square Metre (Nsm-2) or Pascal-Second (Pas). The dimensional formula for viscosity is [ML-1T-1].
Viscosity is influenced by various factors including temperature and pressure. In general, the viscosity of liquids decreases with an increase in temperature, while the viscosity of gases increases with an increase in temperature. This is because, at higher temperatures, the kinetic energy of the molecules increases, causing them to move more freely and reduce the intermolecular forces that contribute to viscosity.
Importance of Viscosity
Viscosity plays a crucial role in many aspects of our daily lives and various industries. Some of the key reasons why viscosity is important are:
- Lubrication: Viscosity is essential for lubrication, ensuring smooth movement and reducing friction between moving parts in machinery and engines. Different types of lubricants with varying viscosities are used depending on the specific application and operating conditions.
- Coating and Paints: Viscosity is carefully controlled in the formulation of paints, varnishes, and coatings to ensure the proper application and uniform coverage on surfaces. The viscosity of these materials affects their flow and spreading properties.
- Food and Beverage: Viscosity is crucial in the food and beverage industry for various reasons. It affects the texture and mouthfeel of products like sauces, syrups, and beverages. Viscosity is also important in controlling the flow and consistency of products during processing and packaging.
- Pharmaceuticals: Viscosity plays a significant role in the formulation and manufacturing of pharmaceutical products such as creams, lotions, and syrups. It helps in determining the ease of application, stability, and shelf life of these products.
- Paints and Inks: Viscosity is a critical factor in the formulation of paints, inks, and dyes. It affects the flow and leveling properties of these materials, ensuring smooth application and even coverage.
- Fuel Efficiency: Viscosity is considered when formulating fuels and lubricants for vehicles. Optimizing viscosity helps reduce friction and improve fuel efficiency by reducing energy losses due to internal friction.
- Biomedical Applications: Viscosity is important in biomedical applications such as drug delivery systems and blood flow within the human body. Understanding and controlling viscosity helps in designing efficient drug delivery systems and studying blood flow characteristics.
These are just a few examples of how viscosity plays a vital role in various industries and everyday applications. Understanding and controlling viscosity is crucial for achieving desired performance and efficiency in many processes and products.
Viscosity Formula
Viscosity is defined as the measure of the ratio of shearing stress to the velocity gradient of a fluid. The formula to calculate viscosity depends on the specific situation and the type of fluid being considered. One common formula to measure viscosity is:
η = 2ga^2(∆ρ) / 9v
Where:
- η represents the viscosity of the fluid
- g is the acceleration due to gravity
- a is the radius of the sphere
- ∆ρ is the difference in density between the fluid and the sphere tested
- v is the velocity of the sphere
This formula is often used to determine the viscosity of a fluid by dropping a sphere into it and measuring its velocity. The viscosity can then be calculated using the above formula.
Types of Viscosity
Viscosity can be classified into two main types: dynamic viscosity (also known as absolute viscosity) and kinematic viscosity.
Dynamic Viscosity
Dynamic viscosity refers to the resistance to flow when an external force is applied to a fluid. It is a measure of the internal friction within the fluid that resists its flow. Dynamic viscosity is typically represented by the symbol η and is measured in units such as Poise or Pascal-Second.
Kinematic Viscosity
Kinematic viscosity, on the other hand, refers to the measure of the resistive flow of a fluid under the weight of gravity. It is obtained by dividing the dynamic viscosity by the density of the fluid. Kinematic viscosity is denoted by the symbol ν and is measured in units such as Stoke or square meter per second (m2/s).
Both dynamic viscosity and kinematic viscosity are important in understanding the flow behavior of fluids and have specific applications depending on the nature of the fluid and the context in which viscosity is being considered.
Coefficient of Viscosity
The coefficient of viscosity, denoted by η, is a measure of the viscous drag or force acting per unit area between layers of a fluid with a unit velocity gradient perpendicular to the direction of flow. It represents the resistance to movement within the fluid.
The coefficient of viscosity can be measured in various units depending on the system of measurement being used. In the CGS system, the unit of the coefficient of viscosity is dynes s cm-2 or Poise. In the SI system, the unit of the coefficient of viscosity is N s m-2 or Pascal-Second.
Variation of Viscosity
The coefficient of viscosity can vary depending on different factors such as temperature and pressure. The effect of temperature on viscosity differs for liquids and gases. In general, the viscosity of liquids decreases with an increase in temperature, while the viscosity of gases increases with an increase in temperature.
The table below provides examples of different fluids and their coefficients of viscosity at various temperatures:
| Fluid | Temperature (in °C) | η (deca-poise) |
|---|---|---|
| Air | 20 | 0.018 × 10-3 |
| Water | 0 | 1.8 × 10-3 |
| Water | 20 | 1.0 × 10-3 |
| Blood | 37 | 0.3 × 10-3 |
| Blood | 72 | 2.7 × 10-3 |
| Engine Oil | 30 | 50 × 10-3 |
| Glycerine | 0 | 1020 |
| Glycerine | 20 | 201.5 |
This table demonstrates the variation in viscosity for different fluids at different temperatures. It highlights the differences in viscosity between fluids and the impact of temperature on their flow properties.
Newtonian and Non-Newtonian Fluids
Fluids can be classified as either Newtonian or non-Newtonian based on their viscosity behavior.
Newtonian Fluids
Newtonian fluids are characterized by a linear relationship between the shear stress and the velocity gradient. In other words, the viscosity remains constant regardless of the shear rate or applied stress. Water is a classic example of a Newtonian fluid, where the viscosity remains constant under different flow conditions.

Non-Newtonian Fluids
Non-Newtonian fluids, on the other hand, exhibit a non-linear relationship between shear stress and velocity gradient. The viscosity of these fluids can change with the applied stress or shear rate. Some common examples of non-Newtonian fluids include ketchup, toothpaste, and paint.
The behavior of non-Newtonian fluids can be further classified into different categories, such as shear-thinning, shear-thickening, and viscoelastic fluids. These fluids have diverse viscosity properties and can exhibit unique flow behaviors under different conditions.
Understanding the rheological behavior of fluids, whether Newtonian or non-Newtonian, is essential in various industries and applications, ranging from food processing to manufacturing and drug formulation.

Measurement of Viscosity
Viscosity can be measured using various methods, depending on the specific requirements and the nature of the fluid being tested. One common method is to use a viscometer, which is a device designed to measure the viscosity of fluids.
One type of viscometer is the U-tube viscometer, also known as a glass capillary viscometer or an Ostwald viscometer. It consists of two reservoir bulbs and a capillary tube. The upper bulb draws the liquid by suction, and the liquid flows down through the capillary into the lower bulb. The time taken for the liquid to pass between two marks on the capillary is proportional to the viscosity of the fluid.
Other methods for measuring viscosity include rotational viscometers, falling ball viscometers, and vibrating viscometers. Each method has its own advantages and limitations, and the choice of the measurement technique depends on factors such as the viscosity range, sample volume, and accuracy requirements.
Applications of Viscosity
Viscosity has numerous practical applications across various industries. Some of the key applications of viscosity include:
- Lubrication: The selection of lubricants with appropriate viscosity is critical for reducing friction and wear in machinery and engines.
- Coating and Paints: Viscosity control is essential in the formulation of paints and coatings to ensure proper flow and coverage.
- Food and Beverage: Viscosity plays a significant role in determining the texture and mouthfeel of food products and beverages.
- Pharmaceuticals: Viscosity affects the stability, formulation, and delivery of pharmaceutical products such as creams, ointments, and syrups.
- Cosmetics: Viscosity is important in cosmetics to ensure the desired texture and application properties of products like lotions, creams, and gels.
- Oil and Gas: Viscosity is crucial in the extraction, refining, and transportation of oil and gas, as it affects flow rates and pumping requirements.
- Polymer Processing: Viscosity control is essential in polymer processing techniques such as extrusion, injection molding, and blow molding.
- Biomedical Engineering: Viscosity plays a role in drug delivery systems and blood flow simulations, aiding in the development of medical devices.
These are just a few examples of how viscosity is applied in various industries, demonstrating its importance in optimizing processes, improving product quality, and enhancing performance.
Bernoulli’s Theorem
Bernoulli’s theorem is a fundamental concept in fluid dynamics that relates the pressure, velocity, and elevation of a fluid in a streamline flow. It states that as the velocity of a fluid increases, the pressure exerted by the fluid decreases, and vice versa. This principle is based on the conservation of energy in fluid flow.
Bernoulli’s theorem can be expressed mathematically as:
P + 1/2ρv^2 + ρgh = constant
Where:
- P is the pressure of the fluid
- ρ is the density of the fluid
- v is the velocity of the fluid
- g is the acceleration due to gravity
- h is the height of the fluid above a reference point
Bernoulli’s theorem has various applications, including in aerodynamics, hydraulics, and the design of fluid flow systems. It helps in understanding the relationship between pressure, velocity, and elevation in fluid flow and is an essential tool in engineering and physics.
How do You Calculate Viscosity?
Viscosity can be calculated using various methods depending on the specific situation and the type of fluid being considered. One common method is to measure the flow of a fluid through a capillary tube and use the dimensions of the tube and the pressure difference to calculate the viscosity.
Another method is to use a viscometer, which is a device specifically designed to measure viscosity. Different types of viscometers, such as rotational viscometers, falling ball viscometers, and vibrating viscometers, can be used depending on the nature of the fluid and the desired accuracy of the measurement.
Additionally, the viscosity of some fluids can be estimated using empirical correlations or models based on experimental data. These models take into account factors such as temperature, pressure, and composition to predict viscosity.
Is High Viscosity Thick or Thin?
High viscosity refers to a fluid that is thick and resistant to flow. It requires more force or energy to make a high-viscosity fluid flow compared to a low-viscosity fluid. Honey is an example of a high-viscosity fluid, while water is an example of a low-viscosity fluid.
The thickness or thinness of a fluid is determined by its viscosity. A high-viscosity fluid is thick and flows slowly, while a low-viscosity fluid is thin and flows quickly.
What is the SI Unit of Viscosity?
The SI unit of viscosity is Pascal-Second (Pa s). It is a derived unit obtained from the SI base units of pressure (Pascal) and time (Second).
Other units commonly used to express viscosity include Poise (P) in the CGS system and Centipoise (cP), which is equal to one hundredth of a Poise. The conversion between these units is as follows:
1 Poise (P) = 100 Centipoise (cP) 1 Pascal-Second (Pa s) = 10 Poise (P)
These units provide a convenient way to express viscosity in different systems of measurement.
Solved Examples on Viscosity
Example 1: There is a 3 mm thick layer of glycerin between a flat plate and a large plate. If the viscosity coefficient of glycerin is 2 N s/m2 and the area of the plane plate is 48 cm. How much force is required to move the plate at a speed of 6 cm/s?
Solution: Given, Thickness of the layer, dx = 3 mm = 3 × 10-3 m. Coefficient of viscosity, η = 2 N s/m2 Change in speed, dv = 6 cm/s = 6 × 10-2 m/s
To calculate the force required, we can use the formula:
F = η A ( dv/dx)
Here, A represents the area of the plate.
By substituting the values into the formula, we get:
F = 2 N s/m2 × 48 × 10-4 m2 × (6 × 10-2 m/s) / (3 × 10-3 m)
Simplifying the equation, we find:
F = 16 N
Therefore, a force of 16 N is required to move the plate at the given speed.
Example 2: A liquid with a viscosity of 0.05 Pa s is flowing through a pipe with a radius of 0.1 m. If the pressure drop across the pipe is 100 Pa, what is the flow rate of the liquid?
Solution: The flow rate of a liquid can be calculated using Poiseuille’s Law, which relates the pressure drop, viscosity, and dimensions of the pipe.
The flow rate (Q) can be calculated using the formula:
Q = (πr^4ΔP) / (8ηl)
Where:
- Q is the flow rate
- r is the radius of the pipe
- ΔP is the pressure drop
- η is the viscosity of the liquid
- l is the length of the pipe
Substituting the given values into the formula, we have:
Q = (π(0.1^4)(100)) / (8(0.05)(1))
Simplifying the equation, we find:
Q ≈ 0.785 m3/s
Therefore, the flow rate of the liquid through the pipe is approximately 0.785 cubic meters per second.
Example 3: A fluid has a dynamic viscosity of 0.1 N s/m2 and a density of 1000 kg/m3. Calculate the kinematic viscosity of the fluid.
Solution: Kinematic viscosity (ν) is calculated by dividing the dynamic viscosity (η) by the density (ρ) of the fluid. The formula is:
ν = η / ρ
Substituting the given values into the formula, we have:
ν = 0.1 N s/m2 / 1000 kg/m3
Simplifying the equation, we find:
ν = 0.0001 m2/s
Therefore, the kinematic viscosity of the fluid is 0.0001 square meters per second.
These solved examples illustrate the application of viscosity concepts in solving real-world problems and calculations.
How Kunduz Can Help You Learn Viscosity?
Kunduz is an online learning platform that offers comprehensive educational resources and interactive tools to help you understand and learn about viscosity. Whether you are a student, educator, or professional in the field, Kunduz provides a wide range of materials, including video lessons, interactive quizzes, practice problems, and more.
With Kunduz, you can explore the principles of viscosity, its measurement techniques, and its practical applications in various industries. The platform offers step-by-step explanations, visual aids, and real-life examples to enhance your understanding and make learning engaging and effective.
By utilizing Kunduz’s resources, you can enhance your knowledge of viscosity and its significance in fluid dynamics, engineering, and everyday life. With a user-friendly interface and accessible content, Kunduz empowers learners to grasp complex concepts and apply them confidently.
