The world of Geometry presents us with a variety of shapes and figures, each with its own unique properties and characteristics. One such fascinating three-dimensional shape is a Cone. It’s quite likely that you’ve come across this shape multiple times in your daily life – From the ice cream cone you devour on a summer day to the traffic cone guiding vehicles on the road.
In this article, we will delve into the mathematical concept of a cone, focusing primarily on understanding its volume. We will discuss the definition of a cone, the formula to calculate its volume, the derivation of this formula, and provide some illustrative examples to enhance your understanding.
An Introduction to Volume of a Cone
The term volume in geometry refers to the amount of space occupied by a three-dimensional shape. In other words, if you think of a shape as a container, the volume would represent the capacity of this container – how much it can hold inside.
When we talk specifically about the volume of a cone, we are referring to the quantity of three-dimensional space enclosed by this cone. The unit of volume is always cubic units, such as cubic centimeters (cm³), cubic meters (m³), cubic inches (in³), and so on.
What is a Cone?
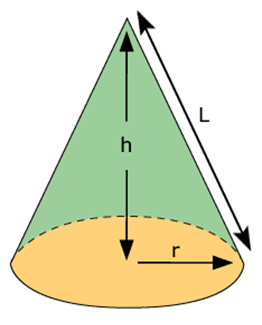
A cone is a three-dimensional geometric figure that tapers smoothly from a flat base (usually circular) to a point called the apex or vertex. The base of the cone is a circle, and the rest of the space is covered by a curved surface that connects the base to the apex.
Cones can be classified into two main types: the right circular cone and the oblique cone. In a right circular cone, the apex is directly above the center of the base, forming a right angle. On the other hand, in an oblique cone, the apex is not directly above the center of the base.
What is the Volume of a Cone?
The volume of a cone is the measure of the amount of space inside the cone. It is calculated as the product of the area of the base and the height of the cone, divided by 3.
The reason behind this division by 3 is that a cone is essentially a pyramid with a circular cross-section. A pyramid’s volume is one-third of the product of its base area and height. Since a cone can be thought of as a special type of pyramid, it follows the same rule.
Volume of a Cone Formula
The volume of a cone is calculated using the following formula:
Volume = V = (1/3) πr²h cubic units
Here,
- r represents the radius of the base of the cone
- h represents the height of the cone
- π is a mathematical constant whose approximate value is 3.14
This formula is applicable for both right circular cones and oblique cones.
Volume of Cone With Height and Radius
When you have the height and the radius of the cone, you can directly substitute these values into the formula to calculate the volume:
Volume = V = (1/3) πr²h cubic units
Volume of Cone With Height and Diameter
If you are given the diameter of the cone instead of the radius, you can still calculate the volume. The radius of a circle (or base of a cone) is always half the diameter. So, you can first calculate the radius and then substitute in the formula:
Volume = V = (1/12) πd²h cubic units
Volume of Cone With Slant Height
Sometimes, you may be provided with the slant height of the cone instead of the actual height. The slant height (represented as L) is the distance from the apex to any point on the base perimeter.
In such cases, you can use the Pythagorean theorem to find the actual height (h) in terms of the radius (r) and the slant height (L):
h = √ (L² – r²)
Once you’ve calculated the height, you can substitute it into the volume formula:
Volume = V = (1/3) πr²√ (L² – r²)
How to Find Volume of Cone?
Finding the volume of a cone is a straightforward process once you know the radius and height of the cone. The steps are as follows:
Step 1: Identify the given parameters. This could be the radius (r), height (h), diameter (d), or slant height (L) of the cone.
Step 2: Apply the appropriate formula based on the given parameters:
- If the radius and height are given, use: V = (1/3) πr²h
- If the diameter and height are given, use: V = (1/12) πd²h
- If the radius and slant height are given, use: V = (1/3) πr² √ (L² – r²)
- If the diameter and slant height are given, use: V = (1/12) πd²√ (L² – (d/2)²)
Step 3: Substitute the given values into the formula and calculate the volume. The result will be in cubic units, as volume is a three-dimensional measurement.
Let’s go through an example to understand this better:
Example: Compute the volume of a cone with a radius of 7 cm and a height of 12 cm.
Solution: Given, r = 7 cm and h = 12 cm. We can use the formula V = (1/3) πr²h. Substituting the values, we get V = (1/3) * 3.14 * (7)² * 12 = 615.44 cm³
Hence, the volume of the cone is 615.44 cubic centimeters.
Derivation of Volume of Cone Formula
The formula for the volume of a cone is derived from the formula for the volume of a cylinder. If you take a cylinder and three cones that have the same height and base radius as the cylinder, you’ll find that the combined volume of the three cones is equal to the volume of the cylinder.
This can be visualized by filling the cones with water and pouring them into the cylinder. You’ll see that it takes exactly three full cones to fill the cylinder to the brim.
This observation leads us to the conclusion that the volume of a cone is one-third the volume of a cylinder with the same base and height. Mathematically, this is represented as:
Volume of a cone = (1/3) * Volume of a cylinder = (1/3) * πr²h
Derivation of the Volume of Cones from the Volume of Cylinders
The formula for the volume of a cone can also be derived using calculus, specifically the method of integration.
Consider a solid right circular cone with base radius r and height h. This cone can be thought of as composed of an infinite number of infinitesimally thin circular disks with varying radii, stacked on top of each other from the base to the apex.
The radius of each disk at a height y from the apex (taking the apex as the origin) is given by (r/h)y (from similar triangles). The volume of each disk is thus π * (r/h)²y² * dy.
Integrating this expression from y = 0 to y = h (from apex to base) gives the total volume of the cone:
V = ∫₀ʰ π * (r/h)²y² dy = (1/3)πr²h
This integral confirms our earlier result that the volume of a cone is one-third the volume of a cylinder with the same base and height.
Types of Cones
Cones can be broadly classified into two categories: right circular cones and oblique cones.
Right Circular Cones
A right circular cone is a cone in which the line drawn from the vertex to the center of the base is perpendicular to the base. This line is also the height (h) of the cone. In a right circular cone, the base is a perfect circle, and the axis is perfectly aligned with the center of the base.

Oblique Cones
Oblique cones are those where the line passing through the vertex and the center of the base is not perpendicular to the base. That means the apex is not aligned directly above the center of the base.
Despite the difference in their shapes, the volume of a right circular cone and an oblique cone with the same base area and height is the same. This is because the volume depends only on the base area and the height, not on the orientation of the height.
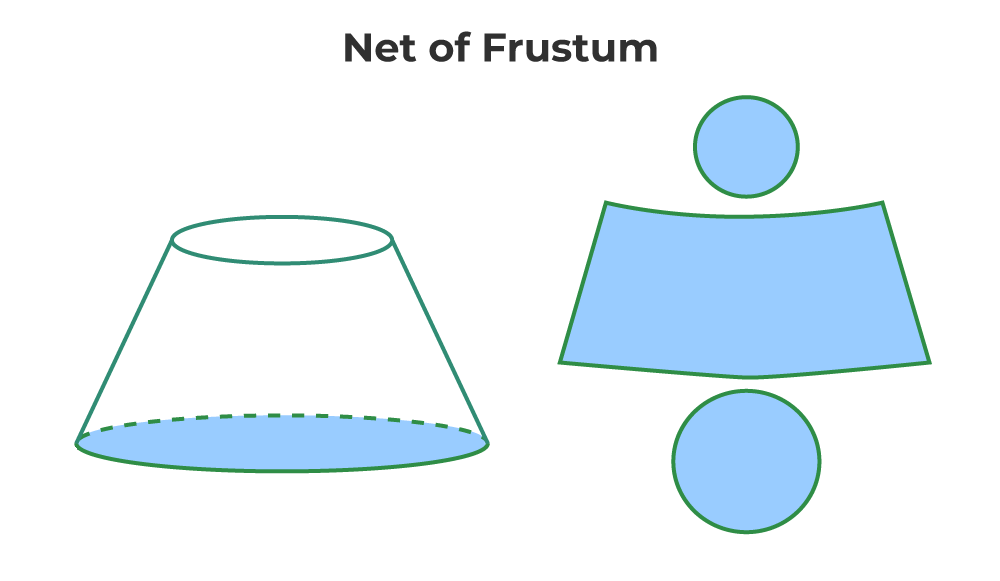
Frustum
A frustum is a part of a cone that is left after cutting out the top part with a plane parallel to the base. It looks like a cone with its apex removed. The volume of a frustum can be found by subtracting the volume of the small cone removed from the volume of the original cone.
Surface Area of a Cone
The surface area of a cone is the sum of the area of the base and the lateral surface area. The formula for the total surface area of a cone is:
Total Surface Area = πr(l + r)
where,
- l is the slant height of the cone
- r is the radius of the base
The formula for the lateral surface area (the area of the side surface) of a cone is:
Lateral Surface Area = πrl
Properties of Cones
Cones have several unique properties that make them stand out among other geometric shapes. Here are a few key properties of cones:
- A cone has only one vertex and one edge.
- A cone has two faces – the base and the curved surface.
- The line from the center of the base to the apex is the height of the cone.
- The line from the apex to any point on the base perimeter is the slant height.
- All cross-sections parallel to the base result in similar circles.
Solved Examples on Volume of a Cone
Now that we have a good understanding of the theory behind the volume of a cone, let’s solve a few example problems to apply this knowledge.
Integer Dimensions
Example 1: Find the volume of a cone with a radius of 6 cm and a height of 8 cm.
Solution: Given r = 6 cm and h = 8 cm. Using the formula V = (1/3)πr²h, we get:
V = (1/3) * 3.14 * (6)² * 8 = 301.44 cm³
Therefore, the volume of the cone is 301.44 cubic centimeters.
Decimal Dimensions
Example 2: Find the volume of a cone with a radius of 3.5 cm and a height of 7.2 cm.
Solution: Given r = 3.5 cm and h = 7.2 cm. Using the formula V = (1/3)πr²h, we get:
V = (1/3) * 3.14 * (3.5)² * 7.2 = 89.43 cm³
Therefore, the volume of the cone is 89.43 cubic centimeters.
Calculate the Volume in Terms of Pi
Example 3: Find the volume of a cone with a radius of 4 cm and a height of 7 cm, expressing the answer in terms of pi.
Solution: Given r = 4 cm and h = 7 cm. Using the formula V = (1/3)πr²h, we get:
V = (1/3) * π * (4)² * 7 = 112π cm³
Therefore, the volume of the cone is 112π cubic centimeters.
Calculate the Volume Given the Diameter
Example 4: Find the volume of a cone with a diameter of 10 cm and a height of 9 cm.
Solution: Given d = 10 cm and h = 9 cm. The radius is half the diameter, so r = d/2 = 10/2 = 5 cm. Using the formula V = (1/3)πr²h, we get:
V = (1/3) * 3.14 * (5)² * 9 = 236.25 cm³
Therefore, the volume of the cone is 236.25 cubic centimeters.
Calculate a Length Given the Volume
Example 5: A cone has a volume of 150π cm³ and a radius of 5 cm. Find the height of the cone.
Solution: Given V = 150π cm³ and r = 5 cm. Using the formula V = (1/3)πr²h and solving for h, we get:
150π = (1/3) * π * (5)² * h
Solving for h, we get h = 18 cm.
Therefore, the height of the cone is 18 centimeters.
Calculate the Radius Given the Volume
Example 6: A cone has a volume of 250 cm³ and a height of 10 cm. Find the radius of the cone.
Solution: Given V = 250 cm³ and h = 10 cm. Using the formula V = (1/3)πr²h and solving for r, we get:
250 = (1/3) * 3.14 * r² * 10
Solving for r, we get r = 3 cm.
Therefore, the radius of the cone is 3 centimeters.
How Kunduz Can Help You Learn the Volume of a Cone?
Kunduz is an online learning portal that offers various resources to help students learn and understand different concepts in mathematics, including the volume of a cone. With Kunduz, you can access interactive learning materials, practice problems, and quizzes that help solidify your understanding of the topic. You can also connect with expert tutors who can assist you with any questions or difficulties you might have. Take advantage of Kunduz’s comprehensive learning resources and make your learning journey smoother and more enjoyable.
