Understanding the concept of a cylinder’s volume is an integral part of mastering geometry, and it is commonly applied in various real-life scenarios. This comprehensive guide will take a deep dive into the volume of a cylinder, discussing its definition, formula, derivation, examples, and fascinating facts.
An Introduction to Volume of a Cylinder
The volume of a cylinder refers to the amount of space within it. This three-dimensional measurement is significant in numerous fields, including mathematics, physics, engineering, and everyday life. For instance, the capacity of a cylindrical water tank or the amount of gas a cylindrical container can hold can be determined using the concept of the volume of a cylinder.
What is a Cylinder?
A cylinder is a three-dimensional geometric shape that consists of two parallel and congruent circles, known as bases, connected by a curved surface. The bases are identical, and the axis, the segment joining the centers of the two bases, is perpendicular to the bases. Cylindrical shapes are prevalent in daily life, seen in objects like cans, pipes, and tanks.
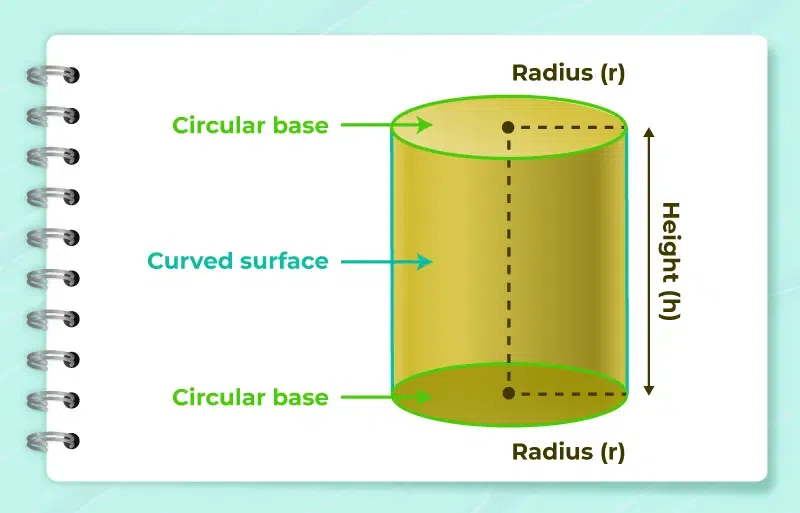
What is the Volume of a Cylinder?
In geometrical terms, the volume of a cylinder is the amount of space it occupies in a three-dimensional plane. This measurement is essentially the cylinder’s capacity, indicating how much of a particular matter, be it solid, liquid, or gas, it can contain. The volume of a cylinder is typically calculated in cubic units such as cubic centimeters (cm³), cubic meters (m³), or cubic feet (ft³).
Volume of a Cylinder Formula
The formula to calculate the volume of a cylinder is derived from its geometrical structure. For a right circular cylinder, the volume is given by the product of the area of its base (a circle) and its height. So, the standard formula for the volume of a cylinder is:
V = πr²h
where:
Vrepresents the Volume of the Cylinderπis a mathematical constant whose approximate value is 3.14159rdenotes the radius of the base of the Cylinderhis the height of the Cylinder
How to Find Volume of a Cylinder?
Calculating the volume of a cylinder is straightforward once you know the formula. Here’s a step-by-step guide:
Step 1: Identify the radius (r) and the height (h) of the cylinder. Ensure both measurements are in the same units.
Step 2: Substitute these values into the formula V = πr²h.
Step 3: Perform the calculation. Multiply the square of the radius by the height and by π.
Step 4: The resulting value is the volume of the cylinder, expressed in cubic units.
Derivation of Volume of Cylinder Formula
The formula for the volume of a cylinder, V = πr²h, can be derived logically. A cylinder can be thought of as numerous superimposed circular disks. Each disk has an area of πr² (the area of a circle), and there are h such disks (where h is the height). So, multiplying the area of each disk by the total number of disks (height) gives the volume of the cylinder.
Volume of a Hollow Cylinder
A hollow cylinder, also known as a cylindrical shell, is a cylinder with an empty interior. Its volume can be found by subtracting the volume of the inner cylinder from the volume of the outer cylinder. The formula for the volume of a hollow cylinder is:
V = π(R² – r²)h
where R represents the outer radius, r is the inner radius, and h is the height.
Volume of an Oblique Cylinder
An oblique cylinder is a cylinder that ‘leans’ to one side, meaning its sides are not perpendicular to its bases. Interestingly, despite this lean, the volume of an oblique cylinder is calculated using the same formula as a right cylinder:
V = πr²h
Volume of Cylinder in Liters
While the formula for the volume of a cylinder provides a result in cubic units, it can be easily converted to liters (for liquid measurements) by using the conversion factor 1 cubic meter = 1000 liters, or 1 cubic centimeter = 1 milliliter.
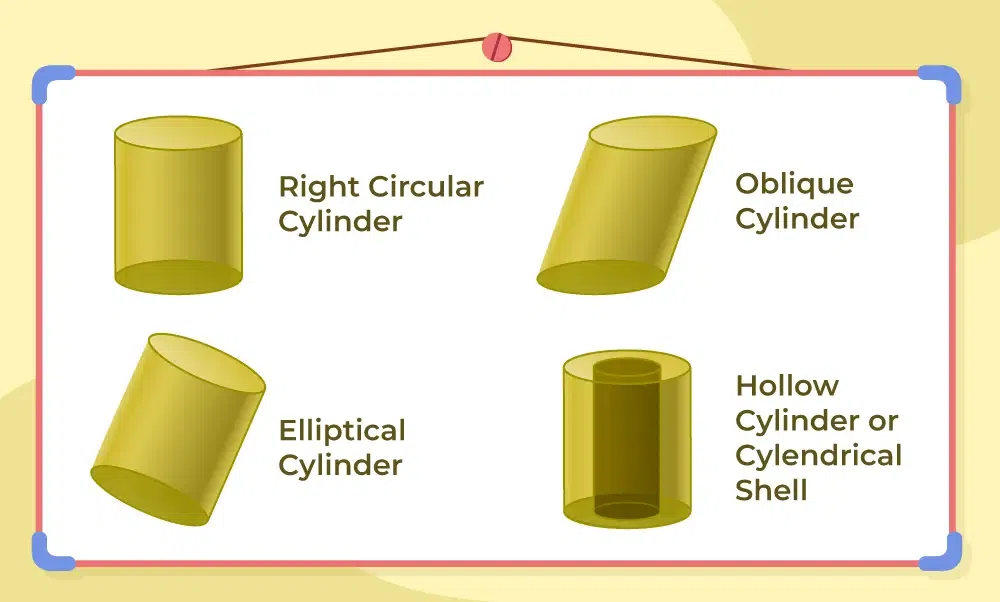
Types of Cylinder
Understanding the different types of cylinders is key to appreciating their volume calculations. Here are the four main types:
Right Circular Cylinder
This is the most common type of cylinder, featuring two circular bases that are parallel and congruent, with all lines on its curved surface perpendicular to the bases.
Oblique Cylinder
An oblique cylinder has a similar structure to a right cylinder, but its sides are slanted, meaning they are not perpendicular to the bases.
Elliptic Cylinder
An elliptic cylinder has elliptical bases instead of circular ones. It has two radii, and its volume formula accommodates these with V = πabh.
Right Circular Hollow Cylinder
This cylinder is essentially a right circular cylinder with an empty interior. It’s like a cylindrical tube or pipe. Its volume formula is V = π(R² - r²)h.
Surface Area of a Cylinder
Apart from the volume, another important property of a cylinder is its surface area. The total surface area of a cylinder includes the areas of its two bases and the area of its curved surface. The formula to calculate the total surface area of a cylinder is:
A = 2πrh + 2πr²
Here, A represents the total surface area, r is the radius, and h is the height of the cylinder.
Properties of a Cylinder
A cylinder has several unique properties that distinguish it from other geometric shapes. Some of these include:
- All cross-sections parallel to the base are congruent.
- The bases of a cylinder are always parallel and identical.
- The axis of a cylinder is a line segment joining the centers of the bases.
- The lateral surface area (not including the bases) of a cylinder is a rectangle when unrolled.
How do You Draw a Cylinder?
Drawing a cylinder involves sketching two parallel ovals (for the bases) and connecting them with straight lines (for the sides). By shading the sides and adding curved lines to the ovals, you can create the illusion of a three-dimensional cylinder.

How do You Calculate the Surface Area to Volume Ratio of a Cylinder?
The surface area to volume ratio of a cylinder can be found by dividing the total surface area by the volume. This ratio is often used in biology and chemistry to understand rates of diffusion and heat loss.
Solved Examples on Volume of a Cylinder
Now that you have a strong understanding of the volume of a cylinder, let’s look at some solved examples:
Example 1: A cylindrical water tank has a radius of 2 meters and a height of 5 meters. What is the volume of the tank in cubic meters?
Using the formula V = πr²h, the volume of the tank is V = π(2)²(5) = 62.83 cubic meters.
Example 2: An elliptic cylinder has base radii of 3 cm and 4 cm, and a height of 10 cm. What is its volume?
For an elliptic cylinder, the volume formula is V = πabh. So, the volume is V = π(3)(4)(10) = 376.99 cubic cm.
Example 3: A hollow cylindrical pipe has an outer radius of 5 cm, an inner radius of 4 cm, and a length of 1 meter (100 cm). What’s the volume of the material used to make the pipe?
The volume of a hollow cylinder is given by V = π(R² - r²)h. Substituting the given values, V = π[(5)² - (4)²](100) = 314.16 cubic cm.
How Kunduz Can Help You Learn the Volume of a Cylinder?
Kunduz offers a wide range of resources to help students grasp the concept of the volume of a cylinder. Additionally, Kunduz’s interactive platform allows students to ask questions and receive personalized answers, further enhancing their understanding of the topic.
