In geometry, a line segment is a fundamental concept that helps us understand the structure and properties of lines. It is a part of a line that has two distinct endpoints. Unlike a line, a line segment has a finite length and can be measured. Line segments play a crucial role in geometry as they form the sides of polygons and are used in various mathematical calculations.
What is the Line Segment?
A line segment can be defined as a straight path that connects two points, known as endpoints. It is the shortest distance between these two points. The length of a line segment is determined by measuring the distance between its endpoints. Line segments are one-dimensional figures and can be represented by a bar symbol (—) on top of the notation, such as AB, to distinguish them from lines and rays.
Line Segment Formula
To find the length of a line segment, we can use the distance formula. The distance formula is derived from the Pythagorean theorem and calculates the distance between two points in a coordinate plane. If we have the coordinates of the two endpoints of a line segment, (x1, y1) and (x2, y2), the formula for finding the length of the line segment is:
d = √[(x2 – x1)^2 + (y2 – y1)^2]
For example, if we have a line segment with endpoints A(2, 4) and B(5, 7), we can use the distance formula to find its length:
d = √[(5 – 2)^2 + (7 – 4)^2] = √[3^2 + 3^2] = √[9 + 9] = √18 ≈ 4.24
Therefore, the length of the line segment AB is approximately 4.24 units.
Measuring Line Segment
By Observation
The simplest method to compare the lengths of line segments is through observation. By visually examining two line segments, we can determine which one is longer or shorter. However, this method is subjective and may not always provide an accurate measurement.
Using Trace Paper
To accurately compare line segments, we can use trace paper. By tracing one line segment and placing it over the other, we can determine which one is longer. This method eliminates any errors caused by visual judgment.
Using Ruler and Divider
Another method to measure line segments is by using a ruler and divider. By placing one needle of the divider at one endpoint and the other needle at the other endpoint, we can measure the length of the line segment on a ruler. This method provides a precise measurement and is commonly used in mathematical calculations.
Line Segment Symbol
A line segment is represented by a bar symbol (—) placed on top of its notation. For example, if a line segment has endpoints P and Q, it can be denoted as PQ. This symbol helps to distinguish line segments from lines and rays.
How To Construct the Line Segment?
To construct a line segment of a specific length, we can use a compass and a ruler. Let’s consider the steps to construct a line segment of length 5 cm:
- Draw a line of any length without a specific measurement.
- Mark a point A on the line, which will serve as the starting point of the line segment.
- Using a ruler, place the pointer of the compass 5 cm apart from the pencil’s lead.
- Place the pointer of the compass at point A and draw an arc on the line using the pencil.
- Mark the point where the arc intersects the line as B.
- AB is the required line segment of length 5 cm.

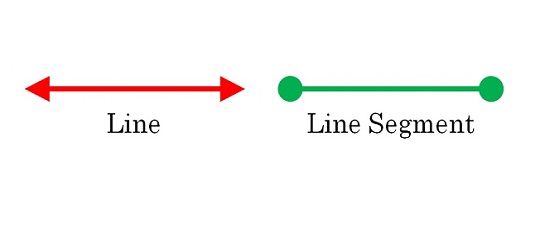
Difference Between Line, Line Segment, and Ray
Lines, line segments, and rays are all one-dimensional figures in geometry, but they have different characteristics.
- A line is a straight path that extends indefinitely in both directions. It has no endpoints.
- A line segment is a part of a line that has two distinct endpoints. It has a finite length.
- A ray is a part of a line that has one endpoint and extends infinitely in one direction.
These distinctions can be represented using different symbols. A line is usually represented by arrows on both ends (↔), a line segment by endpoints (AB), and a ray by an arrow at one end (→).
| Line | Line Segment | Ray |
|---|---|---|
| Extends indefinitely in both directions | Has two distinct endpoints | Has one endpoint |
| Represented by arrows on both ends (↔) | Represented by endpoints (AB) | Represented by an arrow at one end (→) |
Coordinate Plane and Line Segment
In a coordinate plane, line segments can be described using their endpoints’ coordinates. By using the distance formula, we can find the length of a line segment between two points in the coordinate plane.
For example, consider a line segment with endpoints A(2, 4) and B(5, 7). We can calculate its length using the distance formula:
d = √[(5 – 2)^2 + (7 – 4)^2] = √[3^2 + 3^2] = √[9 + 9] = √18 ≈ 4.24
Therefore, the length of the line segment AB is approximately 4.24 units.
Perpendicular Bisector of a Line Segment
The perpendicular bisector of a line segment is a line that intersects the line segment at its midpoint and forms right angles with it. It divides the line segment into two equal parts.
To construct the perpendicular bisector of a line segment, follow these steps:
- Draw the given line segment AB.
- With point A as the center, draw an arc that intersects the line segment.
- With point B as the center, draw an arc with the same radius as step 2.
- The intersection point of the two arcs is the midpoint of the line segment.
- Draw a line passing through the midpoint and perpendicular to the line segment.
- The resulting line is the perpendicular bisector of the line segment.
The perpendicular bisector of a line segment has several properties and applications in geometry, such as determining the center of a circle or finding equidistant points from the endpoints of the line segment.
How to Find the Length of a Line Segment?
There are several methods to find the length of a line segment, depending on the information provided.
Sum of Line Segments
If a longer line segment is composed of smaller line segments, we can find the length of the longer line segment by adding the lengths of the smaller line segments. For example, if line segment AD is composed of line segments AB, BC, and CD, the length of AD can be determined by summing the lengths of AB, BC, and CD.
Sum of Graphing Units
In a graph or coordinate plane, measuring the length of a line segment is straightforward for vertical or horizontal line segments. We can simply count the units between the endpoints. However, for diagonal line segments, we can use the distance formula mentioned earlier.
Counting Method
For non-linear line segments that can be accurately measured by counting, we can count the number of units between the endpoints to determine the length of the line segment. This method is suitable for line segments that are aligned with the graphing units.
Midpoint Formula Method
If we know the coordinates of the endpoints of a line segment, we can use the midpoint formula to find the length. The midpoint formula calculates the coordinates of the midpoint of a line segment, which can then be used to measure the length. The formula for finding the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Once we have the coordinates of the midpoint, we can use the distance formula to find the length of the line segment.
The Distance Formula
The distance formula is used to find the distance between two points in a coordinate plane. It is derived from the Pythagorean theorem and calculates the length of the line segment defined by the two points. The formula is:
d = √[(x2 – x1)^2 + (y2 – y1)^2]
Where (x1, y1) and (x2, y2) are the coordinates of the two points.
How to Find the Length of a Diagonal Line Segment on a Coordinate Plane?
To find the length of a diagonal line segment on a coordinate plane, we can use the distance formula. If we have the coordinates of the two endpoints of the diagonal line segment, we can plug them into the distance formula to calculate its length.
For example, let’s consider a diagonal line segment with endpoints A(2, 4) and B(6, 8). We can use the distance formula to find its length:
d = √[(6 – 2)^2 + (8 – 4)^2] = √[4^2 + 4^2] = √[16 + 16] = √32 ≈ 5.66
Therefore, the length of the diagonal line segment AB is approximately 5.66 units.
Properties of Line Segment
Line segments have several properties that are important to understand:
- Line segments have two distinct endpoints.
- The length of a line segment is the distance between its endpoints.
- Line segments can be added together to form longer line segments.
- Line segments can form the sides of polygons.
- Line segments can be congruent, meaning they have equal lengths.
Solved Examples on Line Segment
Let’s solve a few examples to better understand line segments:
Example 1: Find the length of the line segment with endpoints A(3, 4) and B(7, 10).
Solution: We can use the distance formula to find the length of the line segment.
d = √[(7 – 3)^2 + (10 – 4)^2] = √[4^2 + 6^2] = √[16 + 36] = √52 ≈ 7.21
Therefore, the length of the line segment AB is approximately 7.21 units.
Example 2: Determine the length of the line segment formed by the points C(-1, 2) and D(5, 6).
Solution: Using the distance formula, we can find the length of the line segment.
d = √[(5 – (-1))^2 + (6 – 2)^2] = √[6^2 + 4^2] = √[36 + 16] = √52 ≈ 7.21
Therefore, the length of the line segment CD is approximately 7.21 units.
How Kunduz Can Help You Learn Line Segments?
Kunduz is an innovative platform that offers comprehensive learning resources for various mathematical concepts, including line segments. It provides an interactive learning experience with tailored solutions, detailed explanations, and an extensive database of solved examples.
By leveraging Kunduz’s advanced tools and features, you can quickly grasp the intricacies of line segments, enhancing your mathematical proficiency and boosting your academic performance.
