In the field of trigonometry, the arctan, also known as the inverse tangent function, plays a significant role. It is one of the six inverse trigonometric functions, which include sin⁻¹x, cos⁻¹x, tan⁻¹x, cosec⁻¹x, secx⁻¹x, and cot⁻¹x. While each of these functions has a unique purpose, the arctan specifically focuses on finding the value of an unknown angle based on the tangent ratio of a right-angled triangle.
By definition, the tangent of an angle is equal to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. The arctan function, on the other hand, provides the angle measurement when given the tangent ratio.
Throughout this article, we will explore various aspects of the arctan function, including its formula, graph, identities, domain, range, and its applications in solving trigonometric equations. So let’s dive in and uncover the fascinating world of arctan.
What is Arctan?
Arctan, or arctangent, is an inverse trigonometric function that is denoted as tan⁻¹x or arctan(x). It is the inverse of the tangent function, which means that if the tangent of an angle is equal to x, then the arctan of x will give us the value of that angle.
For example, if we have a right-angled triangle and the tangent of an angle θ is equal to x, we can express this relationship as x = tan θ. By applying the arctan function to both sides of the equation, we can find the value of θ: θ = arctan(x).
The arctan function is widely used in various fields, including navigation, physics, engineering, and mathematics. It allows us to determine unknown angles based on the tangent ratio and is an essential tool in solving trigonometric equations.
For those delving into the intricacies of arctan and its inverse trigonometric functions, our derivative of tan(x) page serves as a valuable reference. It provides deeper insights into the calculus of tangent functions, offering a comprehensive understanding of the relationship between arctan and the derivative of tan(x).
Arctan Formula
The arctan formula is straightforward and can be expressed as follows:
θ = arctan(x)
Here, θ represents the angle whose measure we are trying to find, and x is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
To use the arctan formula, simply substitute the given value of x into the equation and calculate the corresponding angle θ. This formula enables us to determine the angle measure without directly measuring the angle itself.
How To Find the Value of Arctan?
To find the value of arctan, we can use a scientific calculator or refer to an arctan table. Scientific calculators typically have a dedicated arctan button, which allows us to input the value of x and obtain the corresponding angle.
For example, if we want to find the arctan of 0.5, we can simply press the arctan button on the calculator and enter 0.5. The calculator will then provide us with the angle measure in radians or degrees, depending on the calculator settings.
If a scientific calculator is not available, we can also use an arctan table to find the angle. The table lists various values of x and their corresponding arctan values. By locating the given value of x in the table, we can identify the angle associated with it.
Arctan Identities
Arctan has several identities that can be useful in simplifying trigonometric expressions or solving equations. These identities include the following:
- arctan(-x) = -arctan(x): The arctan of a negative value is equal to the negative of the arctan of the positive value.
- tan(arctan(x)) = x: The tangent of the arctan of x is equal to x.
- arctan(tan(x)) = x: The arctan of the tangent of x is equal to x, within a certain range of values.
- arctan(1/x) = π/2 – arctan(x) = arccot(x), if x > 0: The arctan of the reciprocal of x is equal to the complement of the arctan of x, within a certain range of values.
- arctan(1/x) = -π/2 – arctan(x) = arccot(x) – π, if x < 0: Similar to the previous identity, but for negative values of x.
- sin(arctan(x)) = x / √(1 + x²): The sine of the arctan of x is equal to x divided by the square root of 1 plus x squared.
- cos(arctan(x)) = 1 / √(1 + x²): The cosine of the arctan of x is equal to 1 divided by the square root of 1 plus x squared.
- arctan(x) = 2arctan(x / (1 + √(1 + x²))): The arctan of x can be expressed as twice the arctan of x divided by 1 plus the square root of 1 plus x squared.
- arctan(x) = ∫[0 to x] 1 / √(1 + z²) dz: The arctan of x can be obtained by integrating 1 divided by the square root of 1 plus z squared with respect to z.
These identities can be used to simplify complex expressions involving arctan and other trigonometric functions or to solve trigonometric equations.
How To Apply Arctan x Formula?
The arctan formula can be applied in various scenarios, depending on the given information. Let’s explore a couple of examples to understand how to use the arctan formula effectively.
Example 1: Suppose we have a right-angled triangle with a base of 4 units and a height of 3 units. We want to find the angle θ opposite the base.
To apply the arctan formula, we use the ratio of the height to the base, which is 3/4. Plugging this value into the arctan formula, we have:
θ = arctan(3/4)
Using a scientific calculator or arctan table, we find that arctan(3/4) is approximately 36.87 degrees. Therefore, the angle θ is approximately 36.87 degrees.
Example 2: Let’s consider a scenario where we know the tangent of an angle is equal to 0.6. We want to find the value of the angle using the arctan formula.
Using the arctan formula, we have:
θ = arctan(0.6)
Using a scientific calculator or arctan table, we find that arctan(0.6) is approximately 30.96 degrees. Therefore, the angle θ is approximately 30.96 degrees.
These examples demonstrate how the arctan formula can be used to find angle measures based on given ratios or trigonometric functions.
Arctan Domain and Range
The domain and range of a function define the set of possible input and output values, respectively. In the case of the arctan function, the domain and range are determined by the properties of the tangent function.
The tangent function has a periodic nature, which means it repeats itself after certain intervals. As a result, the arctan function needs to be restricted to a specific domain in order to have a unique inverse.
The domain of the arctan function is all real numbers, which means we can input any real number into the arctan function. However, the output or range of the arctan function is limited to the interval (-π/2, π/2). This means that the output of the arctan function will always be between -π/2 and π/2, exclusive.
It’s important to note that the range of the arctan function can also be expressed in degrees, which would be (-90°, 90°). This range represents the valid angle measures that can be obtained using the arctan function.
Additionally, the arctan function can be extended to complex numbers, allowing for a wider range of input values. However, for real numbers, the domain and range remain as mentioned above.
Arctan Table
The arctan function can be represented in tabular form for some common angles. The table below illustrates the arctan values for specific inputs, in both degrees and radians.
| x | arctan(x) (in degrees) | arctan(x) (in radians) |
|---|---|---|
| -∞ | -90° | -π/2 |
| -√3 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -1/√3 | -30° | -π/6 |
| 0 | 0° | 0 |
| 1/√3 | 30° | π/6 |
| 1 | 45° | π/4 |
| √3 | 60° | π/3 |
| ∞ | 90° | π/2 |
This table can be used as a quick reference to determine the arctan of some standard inputs.
Arctan x Properties
The arctan function possesses several properties that can be useful in various mathematical calculations. Let’s explore some of these properties:
- arctan(-x) = -arctan(x): The arctan of a negative value (-x) is equal to the negative of the arctan of the positive value (x). This property indicates that the arctan function is an odd function.
- tan(arctan(x)) = x: The tangent of the arctan of x is equal to x. This property demonstrates the relationship between the tangent and arctan functions.
- arctan(tan(x)) = x, for x in the interval (-π/2, π/2): The arctan of the tangent of x is equal to x, within a specific range of values. This property holds true only when x is between -π/2 and π/2.
- arctan(1/x) = π/2 – arctan(x) = arccot(x), if x > 0: The arctan of the reciprocal of x is equal to the complement of the arctan of x. In other words, if x is positive, the arctan of 1/x is equal to π/2 minus the arctan of x. This property is also related to the arccot function, which is the inverse cotangent.
- arctan(1/x) = -π/2 – arctan(x) = arccot(x) – π, if x < 0: Similar to the previous property, but for negative values of x. If x is negative, the arctan of 1/x is equal to -π/2 minus the arctan of x.
- sin(arctan(x)) = x / √(1 + x²): The sine of the arctan of x is equal to x divided by the square root of 1 plus x squared. This property shows the relationship between the sine and arctan functions.
- cos(arctan(x)) = 1 / √(1 + x²): The cosine of the arctan of x is equal to 1 divided by the square root of 1 plus x squared. This property demonstrates the connection between the cosine and arctan functions.
These properties can be utilized to simplify complex trigonometric expressions or to establish relationships between different trigonometric functions.
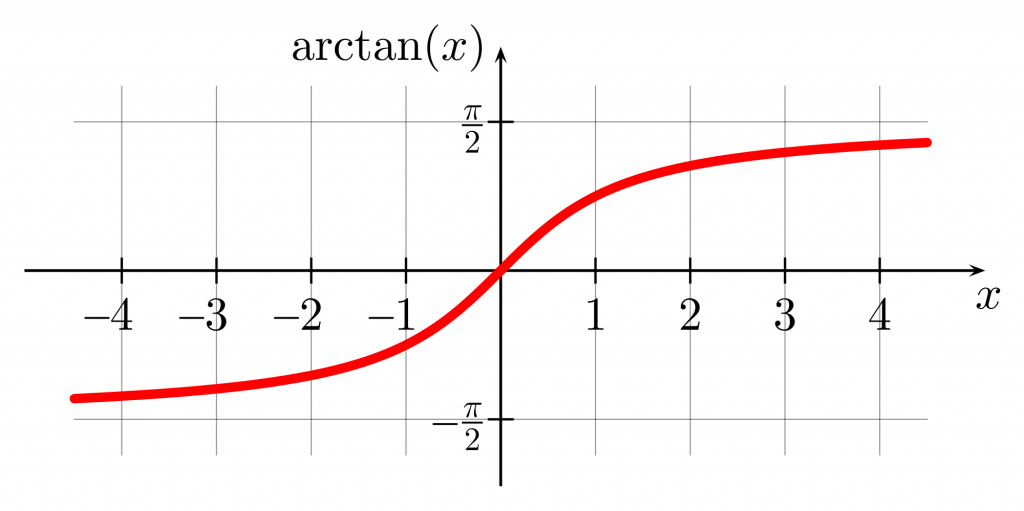
Arctan Graph
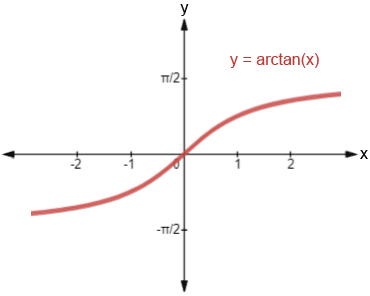
The graph of the arctan function provides a visual representation of its behavior and characteristics. By plotting the arctan values for various input values, we can observe the shape and properties of the function.
The graph of the arctan function has a distinct shape, with a range limited to the interval (-π/2, π/2). As the input values increase or decrease, the corresponding arctan values approach the boundaries of this range. The graph exhibits a horizontal asymptote at y = -π/2 as the input approaches negative infinity, and a horizontal asymptote at y = π/2 as the input approaches positive infinity.
Furthermore, the graph of the arctan function is symmetrical about the line y = x, which means that if we reflect a point across this line, the resulting point will have the same arctan value. This symmetry is a result of the inverse nature of the arctan function.
The arctan graph also demonstrates that the arctan function is a one-to-one function, meaning that each input value corresponds to a unique output value. This property enables us to use the arctan function to find angle measures based on given ratios.
Arctan Derivative
The derivative of a function represents the rate at which the function changes with respect to its input. In the case of the arctan function, its derivative can be calculated using calculus.
The derivative of the arctan function, denoted as d/dx(arctan(x)) or arctan'(x), can be expressed as follows:
d/dx(arctan(x)) = 1 / (1 + x²)
This derivative formula indicates that the rate of change of the arctan function with respect to x is equal to 1 divided by 1 plus x squared.
The derivative of the arctan function is derived using the chain rule of differentiation. By applying the chain rule to the derivative of the tangent function, we can obtain the derivative of the arctan function.
The derivative of the arctan function is particularly useful in calculus and related fields, where it is used to calculate rates of change and solve various mathematical problems.
Integral of Arctan x
The integral of a function represents the area under the curve of the function. In the case of the arctan function, its integral can be calculated using integration techniques.
The integral of the arctan function, denoted as ∫ arctan(x) dx, can be expressed as follows:
∫ arctan(x) dx = x * arctan(x) – ∫ (1 / (1 + x²)) dx
This integral formula indicates that the integral of the arctan function is equal to x multiplied by arctan(x) minus the integral of 1 divided by 1 plus x squared with respect to x.
The integral of the arctan function can be obtained by applying integration techniques, such as substitution or integration by parts. It is particularly useful in calculus and related fields, where it is used to calculate areas, volumes, and solve various mathematical problems.
Taylor Series for Arctan(x)
The Taylor series for a function provides a power series representation of the function. The Taylor series for arctan x is given by arctan x = x - x³/3 + x⁵/5 - x⁷/7 + x⁹/9 - ... for -1 ≤ x ≤ 1. The general term of the series can be written as (-1)^n * x^(2n+1) / (2n+1), where n is a non-negative integer.
Power Series of Arctan(x)
The power series of a function provides a series representation of the function that involves powers of the variable x. The power series of arctan x is given by arctan x = ∑_{n=0}^{∞} (-1)^n * x^(2n+1) / (2n+1) for -1 ≤ x ≤ 1. This is the same as its Taylor series.
Maclaurin Series for Arctan(x)
The Maclaurin series is a special case of the Taylor series where the series is expanded about the point x=0. The Maclaurin series for arctan x is the same as its Taylor series, which is arctan x = x - x³/3 + x⁵/5 - x⁷/7 + x⁹/9 - ... for -1 ≤ x ≤ 1.
Arctan of Infinity
The arctan function has a specific behavior when the input approaches infinity or negative infinity. As the input value becomes extremely large, the arctan function approaches its maximum value of π/2 or 90 degrees.
When the input approaches negative infinity, the arctan function approaches its minimum value of -π/2 or -90 degrees. This behavior can be observed in the graph of the arctan function, where the function approaches the horizontal asymptotes y = π/2 and y = -π/2 as the input value increases or decreases indefinitely.
This property of the arctan function is important to consider when working with large input values or when analyzing the behavior of trigonometric functions in the context of limits and calculus.
Solved Examples of Arctan
To further understand the application of the arctan function, let’s explore a few solved examples.
Example 1: Find the value of arctan(0).
Solution: Since the tangent of 0 is 0, we can use the arctan function to find the angle whose tangent is 0. By applying the arctan function to 0, we find that arctan(0) is equal to 0.
Therefore, the value of arctan(0) is 0.
Example 2: Find the value of arctan(1).
Solution: The tangent of an angle is equal to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. Therefore, if the tangent of an angle is 1, it means that the side opposite the angle is equal in length to the side adjacent to the angle.
By applying the arctan function to 1, we can find the angle whose tangent is 1. We find that arctan(1) is equal to π/4 or 45 degrees.
Therefore, the value of arctan(1) is π/4 or 45 degrees.
These examples demonstrate how the arctan function can be used to find angle measures based on given ratios and trigonometric values.
Is arctan the Same as Inverse tan?
Yes, the arctan function is the same as the inverse tangent function. The terms “arctan” and “inverse tan” are used interchangeably to refer to the same mathematical concept.
Both terms represent the inverse of the tangent function, where the arctan or inverse tan function takes the ratio of opposite and adjacent sides of a right-angled triangle and provides the angle measurement.
Therefore, arctan(x) = inverse tan(x), and they can be used interchangeably in mathematical calculations.
What is the Exact Value of Arctan (-1)?
The exact value of arctan (-1) can be found using the properties of the arctan function. Since the tangent of π/4 is equal to 1, we can conclude that the arctan of 1 is equal to π/4.
By applying the property arctan(-x) = -arctan(x), we can find that arctan(-1) is equal to the negative of arctan(1), which is -π/4.
Therefore, the exact value of arctan(-1) is -π/4 or approximately -0.7854 radians.
Using Special Angles to Find Arctan
Special angles, such as 0 degrees, 30 degrees, 45 degrees, 60 degrees, and 90 degrees, have specific trigonometric values that can be used to find the value of the arctan function.
For example, the arctan of 0 is equal to 0, as the tangent of 0 is 0. The arctan of 1 is equal to π/4 or 45 degrees, as the tangent of π/4 is 1. Similarly, the arctan of √3 is equal to π/3 or 60 degrees, as the tangent of π/3 is √3.
These special angles can be used as reference points to determine the values of the arctan function for specific input values. By understanding the trigonometric ratios of these angles, we can find the corresponding values of the arctan function.