In the realm of mathematics, exponents play a crucial role in simplifying and expressing large numbers. When faced with numbers like 10, 29, or even 135000, it can be challenging to comprehend their magnitude at a glance. However, by utilizing exponents, these numbers can be represented in a more concise and manageable manner.
Exponents, also known as indices or powers, provide a shorthand method for indicating repeated multiplication of a number by itself. The concept of an exponent involves two fundamental components: the base and the exponent itself. The base represents the number being multiplied, while the exponent indicates the number of times the base is multiplied by itself. For instance, in the expression 8^3, the base is 8, and the exponent is 3. This can be interpreted as 8 multiplied by itself three times, resulting in the value 512.
What is Exponent?
In its essence, an exponent denotes the number of times a base is multiplied by itself. The base can be any integer, fraction, or decimal, while the exponent can take on any numerical value, whether positive or negative. Exponents are used to simplify and condense the representation of large numbers, making mathematical calculations and comparisons more manageable.
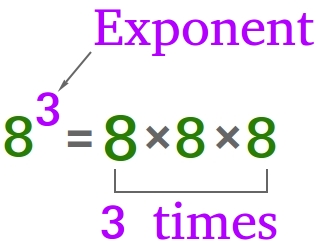
Exponents Formulas
When working with exponents, there are several formulas or laws that govern their manipulation. These laws of exponents provide a set of rules for solving problems involving exponents. By familiarizing ourselves with these formulas, we can navigate through exponent-related calculations more effectively.
- Law of Product: When multiplying two exponential expressions with the same base, we add their exponents. This can be expressed as am × an = am + n, where m and n are real numbers.
- Law of Quotient: When dividing two exponential expressions with the same base, we subtract their exponents. It can be represented as am/an = am – n, where m and n are real numbers and a is a non-zero term.
- Law of Negative Exponent: A negative exponent can be transformed into a positive exponent by taking the reciprocal of the base. It follows the rule a-m = 1/am, where a is a non-zero number, and m is a real number.
- Law of Zero Exponent: Any number raised to the power of zero equals 1, given by a^0 = 1, where a is a non-zero number.
- Law of Power of a Product: When multiplying different bases with the same exponent, we multiply the bases together and keep the exponent the same. It can be stated as (ab)^m = am × bm.
- Law of Power of a Power: When a power is raised to another power, we multiply the exponents. This is represented as (am)^n = amn.
- Law of Power of a Quotient: When dividing different bases with the same exponent, we divide the bases first and then apply the exponent. It is given by (a/b)^m = am/bm, where a and b are non-zero terms.
By utilizing these exponent laws, we can simplify and solve various exponent-related problems efficiently.
Exponent Symbol
In mathematical notation, the exponent is often denoted by using a superscript or a caret symbol. The superscript format involves placing the base number followed by the exponent written in a smaller font slightly above the baseline. For example, 8^3 represents the base 8 raised to the power of 3. Alternatively, the caret symbol (^) can be used to separate the base and the exponent. Both notations convey the same meaning and can be used interchangeably.
Types of Exponents
Exponents come in various types, each with its unique characteristics and applications. Let’s explore the different types of exponents:
Rational Exponent
A rational exponent is an exponent expressed as a fraction or a ratio. Rational exponents are closely related to roots and can be used to represent square roots, cube roots, and nth roots. To simplify a number with a rational exponent, the denominator of the exponent is taken outside the root, while the base number remains inside, raised to the power of the numerator. This can be understood through examples:
- The expression 2^(1/2) represents the square root of 2. When simplified, it becomes sqrt(2) ≈ 1.414.
- Similarly, the expression 2^(1/3) represents the cube root of 2, which is approximately 1.26.
Rational exponents provide a flexible way to represent fractional powers and are widely used in advanced mathematics and scientific calculations.
Positive Exponent
A positive exponent is a straightforward representation of multiplying a base number by itself a certain number of times. When the exponent is positive, we perform repeated multiplication of the base number, starting from 1 as the first power. For example, 3^4 is equivalent to multiplying 3 by itself four times:
3^4 = 3 × 3 × 3 × 3 = 81
Positive exponents indicate the number of times the base is multiplied by itself, allowing for efficient representation of large numbers and simplification of calculations.
Negative Exponent
A negative exponent indicates the reciprocal of a number raised to a positive exponent. In other words, it signifies dividing 1 by the base number raised to the positive power. For example, 2^(-3) can be expressed as:
2^(-3) = 1 / (2^3) = 1 / (2 × 2 × 2) = 1 / 8 ≈ 0.125
Negative exponents are useful in expressing fractions and decimal numbers, making it easier to work with numbers of varying scales.
Zero Exponent
A zero exponent is a special case where any non-zero number raised to the power of zero equals 1. This rule applies universally and is true for all non-zero bases. For example:
5^0 = 1 10^0 = 1 1000^0 = 1
The zero exponent property is a fundamental concept in exponentiation and is based on the notion that any number multiplied by 1 remains unchanged.
Laws of Exponents
The laws of exponents, also known as the rules of exponents or exponentiation, provide a set of guidelines for manipulating expressions involving exponents. These laws help simplify calculations and solve problems more efficiently. Let’s explore the different laws of exponents:
Law of Product
The law of product states that when multiplying two exponential expressions with the same base, we add their exponents. In other words, the exponent of the product is equal to the sum of the exponents. The base remains the same. This can be expressed as:
a^m * a^n = a^(m + n)
For example, if we have the expression 2^3 * 2^4, we can apply the law of product:
2^3 * 2^4 = 2^(3 + 4) = 2^7 = 128
The law of product allows us to simplify and combine exponential expressions with the same base.
Law of Quotient
The law of quotient states that when dividing two exponential expressions with the same base, we subtract their exponents. In other words, the exponent of the quotient is equal to the difference of the exponents. The base remains the same. This can be expressed as:
a^m / a^n = a^(m – n)
For example, if we have the expression 5^6 / 5^3, we can apply the law of quotient:
5^6 / 5^3 = 5^(6 – 3) = 5^3 = 125
The law of quotient allows us to simplify and divide exponential expressions with the same base.
Law of Negative Exponent
The law of negative exponent states that when an exponent is negative, we can convert it into a positive exponent by taking the reciprocal of the base. In other words, a negative exponent indicates the reciprocal of the base raised to the positive exponent. This can be expressed as:
a^(-m) = 1 / a^m
For example, if we have the expression 2^(-3), we can apply the law of negative exponent:
2^(-3) = 1 / 2^3 = 1 / (2 * 2 * 2) = 1 / 8 = 0.125
The law of negative exponent allows us to simplify and transform negative exponents into positive exponents.
Law of Zero Exponent
The law of zero exponent states that any non-zero number raised to the power of zero is equal to 1. In other words, any base with an exponent of zero results in a value of 1. This can be expressed as:
a^0 = 1
For example, if we have the expression 7^0, we can apply the law of zero exponent:
7^0 = 1
The law of zero exponent allows us to simplify and evaluate expressions involving exponentiation.
Law of Power of a Product
The law of power of a product states that when raising a product of two bases to a power, we can distribute the power to each base. In other words, the exponent is multiplied by each base. This can be expressed as:
(a * b)^m = a^m * b^m
For example, if we have the expression (2 * 3)^2, we can apply the law of power of a product:
(2 * 3)^2 = 2^2 * 3^2 = 4 * 9 = 36
The law of power of a product allows us to simplify and distribute the exponent to each base when dealing with a product raised to a power.
Law of Power of a Quotient
The law of power of a quotient states that when raising a quotient of two bases to a power, we can distribute the power to both the numerator and denominator. In other words, the exponent is applied to both the numerator and denominator separately. This can be expressed as:
(a / b)^m = a^m / b^m
For example, if we have the expression (4 / 2)^3, we can apply the law of power of a quotient:
(4 / 2)^3 = 4^3 / 2^3 = 64 / 8 = 8
The law of power of a quotient allows us to simplify and apply the exponent to both the numerator and denominator when dealing with a quotient raised to a power.
By understanding and applying these laws of exponents, we can simplify and solve complex exponential expressions more effectively.
Negative Exponents
Negative exponents play a significant role in exponentiation. They allow us to represent fractions, solve equations, and simplify complex expressions. A negative exponent indicates the reciprocal of a number raised to the corresponding positive exponent. In other words, to convert a negative exponent to a positive exponent, we take the reciprocal of the base and apply the positive exponent. This concept is particularly useful when dealing with fractions and decimal numbers.
For example, let’s consider the expression 2^(-3). To convert this to a positive exponent, we take the reciprocal of 2, which is 1/2, and apply the positive exponent 3:
2^(-3) = (1/2)^3 = 1/2 * 1/2 * 1/2 = 1/8
Negative exponents allow us to express values as fractions or decimals, making calculations and comparisons more manageable.
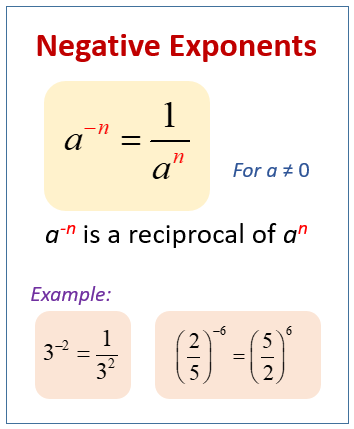
Exponents with Fractions
Exponents can also be expressed as fractions, which are commonly known as fractional exponents. These exponents are closely related to roots, such as square roots, cube roots, and nth roots. Fractional exponents provide a flexible way to represent fractional powers and are widely used in advanced mathematics and scientific calculations.
To simplify a number with a fractional exponent, we can convert it into a radical or root form. The numerator of the fractional exponent represents the power, while the denominator represents the root. For example:
2^(1/2) represents the square root of 2, which is approximately equal to 1.414. 2^(1/3) represents the cube root of 2, which is approximately equal to 1.26.
Fractional exponents allow us to perform calculations involving fractional powers and are essential in various mathematical and scientific applications.
Decimal Exponents
In addition to whole number and fractional exponents, we can also have decimal exponents. Decimal exponents are used to represent numbers that are not whole or fractional powers. When dealing with decimal exponents, it is often more practical to work with approximations or scientific notation to express the values.
For example, the expression 10^1.5 can be approximated as 31.62, which is the square root of 10 multiplied by 10.
Decimal exponents are commonly used in scientific notation, where numbers are expressed as a product between a decimal number and a power of 10. This notation is useful for representing very large or very small numbers in a concise and standardized format.
Exponent Table
To further understand the concepts of exponents, it is helpful to refer to an exponent table that provides a comprehensive overview of different exponents and their corresponding values. The exponent table displays the base, the expression, the expanded form, and the simplified value for each exponent.
| Type of Exponent | Expression | Expanded Form | Simplified Value |
|---|---|---|---|
| Zero exponent | 7^0 | 1 | 1 |
| Positive exponent | 3^4 | 3 * 3 * 3 * 3 | 81 |
| Negative exponent | 2^(-3) | 1 / (2 * 2 * 2) | 1/8 |
The exponent table provides a visual representation of the different types of exponents and their corresponding values, allowing for a better understanding of their properties and applications.
Scientific Notation with Exponents
Scientific notation is a method of expressing very large or very small numbers using exponents. It represents a number as a product of a number between 1 and 10 and a power of 10. For example, the number 2000 can be written in scientific notation as 2 * 10^3.
Importance of Exponents
Exponents play a crucial role in mathematics by enabling the concise representation of large or small numbers. They simplify complex calculations involving repeated multiplication and make it easier to manipulate numbers in scientific notation.
How To Type and Read an Exponent?
Typically, an exponent is represented as a small superscript number placed on the upper right of the base number. However, in digital communication, the caret symbol (^) is often used to denote an exponent. For instance, the number 5 raised to the power of 3 is written as 5^3.
When reading exponents, we say “raised to the power of”. For example, 2^3 is read as “two raised to the power of three”.
Solved Examples on Exponents
Let’s illustrate the concept with a few examples:
Example 1: Evaluate 3^4.
Solution: 3^4 = 3 * 3 * 3 * 3 = 81.
Example 2: Simplify 2^-3.
Solution: 2^-3 = 1/(2^3) = 1/8.
Example 3: Solve the expression 4^(1/2).
Solution: 4^(1/2) signifies the square root of 4, which equals 2.
Example 4: Express the number 1000000 in scientific notation.
Solution: 1000000 can be written as 1 * 10^6 in scientific notation.
How Kunduz Can Help You Learn Exponents?
Mastering the concept of exponents can be made simpler with Kunduz’s interactive learning platform. It provides a wealth of resources, including well-structured lessons, practice problems, and instant solutions to your doubts. With Kunduz, you can learn and understand exponents at your own pace and convenience.
