In the realm of mathematics and geometry, understanding the concept of a quadrant is essential. A quadrant can be defined as a region or section of a cartesian plane that is formed when the x-axis and y-axis intersect each other at a right angle. This intersection creates four distinct regions, which are aptly referred to as quadrants. Quadrants are an integral part of coordinate geometry, allowing us to locate and analyze points within a plane.
What is Quadrant?
A quadrant is a specific region within a cartesian plane that is formed by the intersection of the x-axis and y-axis. The cartesian plane, also known as the coordinate plane, is a two-dimensional plane that consists of two perpendicular lines – the x-axis (horizontal line) and the y-axis (vertical line). These axes intersect at a point called the origin, which is denoted by the coordinates (0,0). The four quadrants are numbered in a counterclockwise direction, starting from the top right and moving towards the top left, bottom left, and finally the bottom right.
What is Origin?
The origin is the point of intersection between the x-axis and y-axis in a cartesian plane. It is denoted by the coordinates (0,0) and serves as the reference point for locating other points on the plane. The origin is located at the center of the coordinate plane and has a significant role in determining the position of points in relation to the axes and quadrants.

What is Cartesian Plane?
The cartesian plane, also known as the coordinate plane, is a two-dimensional plane formed by the intersection of the x-axis and y-axis. It is named after the French mathematician and philosopher René Descartes, who introduced the concept of using coordinates to represent points in space. The cartesian plane provides a systematic way to represent and analyze geometric figures, equations, and mathematical functions. It is divided into four quadrants, which play a crucial role in determining the position of points on the plane.
Four Quadrants in Coordinate Plane
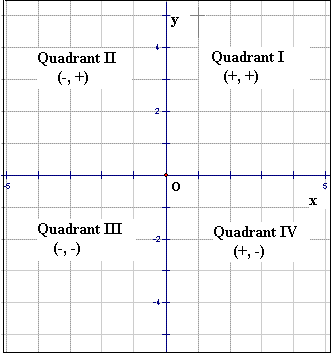
The cartesian plane is divided into four quadrants based on the signs of the coordinates of points within the plane. Each quadrant has its unique characteristics and represents a specific combination of positive and negative values for the x-axis and y-axis.
1st Quadrant
The first quadrant is located in the upper right-hand corner of the cartesian plane. In this quadrant, both the x-coordinate and y-coordinate of points are positive. It represents the top-right portion of the plane and is denoted by the Roman numeral “I”.
2nd Quadrant
The second quadrant is situated in the upper left-hand corner of the cartesian plane. In this quadrant, the x-coordinate is negative, while the y-coordinate is positive. It represents the top-left portion of the plane and is denoted by the Roman numeral “II”.
3rd Quadrant
The third quadrant is positioned in the lower left-hand corner of the cartesian plane. In this quadrant, both the x-coordinate and y-coordinate of points are negative. It represents the bottom-left portion of the plane and is denoted by the Roman numeral “III”.
4th Quadrant
The fourth quadrant is found in the lower right-hand corner of the cartesian plane. In this quadrant, the x-coordinate is positive, while the y-coordinate is negative. It represents the bottom-right portion of the plane and is denoted by the Roman numeral “IV”.
These four quadrants provide a systematic way to determine the position of points within the cartesian plane, enabling us to analyze and solve various mathematical problems.
Sign Convention in Quadrants
The sign convention in quadrants is essential for understanding the signs of the coordinates in each quadrant. It helps us determine whether a point is located in the positive or negative region of the cartesian plane.
| Quadrants | X-coordinate | Y-coordinate |
|---|---|---|
| 1st Quadrant | Positive (+) | Positive (+) |
| 2nd Quadrant | Negative (-) | Positive (+) |
| 3rd Quadrant | Negative (-) | Negative (-) |
| 4th Quadrant | Positive (+) | Negative (-) |
In the first quadrant, both the x-coordinate and y-coordinate of points are positive. In the second quadrant, the x-coordinate is negative, while the y-coordinate is positive. In the third quadrant, both the x-coordinate and y-coordinate of points are negative. Lastly, in the fourth quadrant, the x-coordinate is positive, while the y-coordinate is negative.
This sign convention allows us to determine the position of a point within a quadrant based on the signs of its coordinates.
Graph of Quadrants
The graph of quadrants visually represents the four quadrants within the cartesian plane. It provides a clear visualization of the positive and negative regions of the plane and helps us understand the positioning of points in each quadrant. The graph is divided into four sections, with the x-axis and y-axis intersecting at the origin (0,0). The four quadrants are labeled with Roman numerals and are numbered in a counterclockwise direction.
Plotting Points on Quadrants
Plotting points on quadrants is a fundamental skill in coordinate geometry. It allows us to represent the position of a point within the cartesian plane using its coordinates. To plot a point on a quadrant, we need to consider the signs of its x-coordinate (abscissa) and y-coordinate (ordinate).
The abscissa represents the horizontal distance of the point from the y-axis and is denoted by the x-coordinate. A positive abscissa means the point is located to the right of the origin, while a negative abscissa means the point is located to the left of the origin.
The ordinate represents the vertical distance of the point from the x-axis and is denoted by the y-coordinate. A positive ordinate means the point is located above the origin, while a negative ordinate means the point is located below the origin.
By analyzing the signs of the x-coordinate and y-coordinate, we can determine the quadrant in which the point lies and plot it accordingly on the cartesian plane.
Trigonometric values in Different Quadrants
Trigonometry, a branch of mathematics that deals with the relationships and properties of triangles, relies on the concept of quadrants. The values of various trigonometric functions differ depending on the quadrant in which the angle lies.
| Trigonometric Function | 1st Quadrant | 2nd Quadrant | 3rd Quadrant | 4th Quadrant |
|---|---|---|---|---|
| Sin | Positive (+) | Positive (+) | Negative (-) | Negative (-) |
| Cos | Positive (+) | Negative (-) | Negative (-) | Positive (+) |
| Tan | Positive (+) | Negative (-) | Positive (+) | Negative (-) |
| Cot | Positive (+) | Negative (-) | Positive (+) | Negative (-) |
| Sec | Positive (+) | Negative (-) | Negative (-) | Positive (+) |
| Cosec | Positive (+) | Positive (+) | Negative (-) | Negative (-) |
In the first quadrant, all trigonometric ratios are positive. In the second quadrant, sine and cosecant are positive, while cosine and secant are negative. In the third quadrant, tangent and cotangent are positive, while cosine and secant are negative. In the fourth quadrant, sine and cosecant are negative, while cosine and secant are positive.
These trigonometric values play a crucial role in solving various mathematical problems and analyzing angles within the cartesian plane.
Abscissa and Ordinate in Quadrants
The abscissa and ordinate are important concepts in coordinate geometry, specifically in relation to quadrants. They represent the x-coordinate and y-coordinate of a point, respectively, and provide information about its position within the cartesian plane.
The abscissa represents the horizontal distance of a point from the y-axis. It indicates whether the point is located to the right or left of the origin. A positive abscissa means the point is to the right of the origin, while a negative abscissa means the point is to the left of the origin.
The ordinate represents the vertical distance of a point from the x-axis. It indicates whether the point is located above or below the origin. A positive ordinate means the point is above the origin, while a negative ordinate means the point is below the origin.
By considering the signs of the abscissa and ordinate, we can determine the quadrant in which a point lies and precisely locate it within the cartesian plane.
How to Plot Points on Quadrants?
Plotting points on quadrants is a straightforward process that involves considering the signs of the coordinates and using the origin as a reference point. By following a few simple steps, we can accurately plot a point within the cartesian plane.
Step 1: Identify the x-coordinate of the point. If it is positive, move to the right of the origin. If it is negative, move to the left of the origin.
Step 2: Identify the y-coordinate of the point. If it is positive, move upward from the origin. If it is negative, move downward from the origin.
Step 3: Locate the point by combining the movements in the x and y directions. The point will be at the intersection of the x-coordinate and y-coordinate.
By following these steps and considering the signs of the coordinates, we can effectively plot points in their respective quadrants on the cartesian plane.
Properties of Quadrants
Each quadrant within the cartesian plane has its own unique properties based on the signs of the coordinates. These properties help us understand the positioning of points within each quadrant and provide insights into their characteristics.
- First Quadrant:
- Both the x-coordinate and y-coordinate of points in the first quadrant are positive.
- Points in this quadrant are located in the top-right portion of the cartesian plane.
- The first quadrant is denoted by the Roman numeral “I”.
- Second Quadrant:
- The x-coordinate is negative, while the y-coordinate is positive in the second quadrant.
- Points in this quadrant are located in the top-left portion of the cartesian plane.
- The second quadrant is denoted by the Roman numeral “II”.
- Third Quadrant:
- Both the x-coordinate and y-coordinate of points in the third quadrant are negative.
- Points in this quadrant are located in the bottom-left portion of the cartesian plane.
- The third quadrant is denoted by the Roman numeral “III”.
- Fourth Quadrant:
- The x-coordinate is positive, while the y-coordinate is negative in the fourth quadrant.
- Points in this quadrant are located in the bottom-right portion of the cartesian plane.
- The fourth quadrant is denoted by the Roman numeral “IV”.
Understanding these properties allows us to determine the position of points within the cartesian plane and analyze their characteristics within their respective quadrants.
Solved Examples on Quadrant
Let’s explore some solved examples to further understand how to locate points within quadrants on the cartesian plane.
Example 1: Plot the point A(3, -4) and identify its quadrant.
Solution: The point A has an x-coordinate of 3, indicating a position to the right of the origin. The y-coordinate is -4, indicating a position below the origin. Therefore, the point A lies in the fourth quadrant.
Example 2: Determine the quadrant in which the point P(-5, 2) is located.
Solution: The x-coordinate of the point P is -5, indicating a position to the left of the origin. The y-coordinate is 2, indicating a position above the origin. Therefore, the point P lies in the second quadrant.
These examples demonstrate how to determine the quadrant of a point based on its coordinates and accurately locate it within the cartesian plane.
How Kunduz Can Help You Learn Quadrant?
At Kunduz, we understand the importance of mastering coordinate geometry, including the concept of quadrants. We strive to provide comprehensive and accessible learning resources to help students enhance their mathematical skills and excel in their academic pursuits.
Whether you’re a student seeking assistance with homework or a teacher looking for engaging teaching resources, Kunduz is here to support you on your learning journey. Join us today and discover the power of interactive and effective learning.
