Oran Nedir?
Matematikte oran, iki veya daha fazla sayının birbirine olan bağlantısını ifade eden bir kavramdır. Oran, genellikle a/b veya a:b şeklinde gösterilir, burada “a” ve “b” sayısal değerlerdir. Oran, iki miktar arasındaki göreceli büyüklüğü veya küçüklüğü ifade eder.
Örneğin, 2/3 oranı, bir miktarın diğerinden 2 kat daha büyük olduğunu belirtir. Eğer iki sayı arasındaki oran 1 ise, bu durumda sayılar eşittir. Oranlar, genellikle orantılarla ilişkilidir. Bir oranın tersi de alınabilir, yani a/b oranının tersi b/a şeklinde ifade edilir.
Matematikte oranlar, orantılar, oran orantıları gibi konseptler, problemleri çözme, modelleme ve karşılaştırma süreçlerinde kullanılır. Oranlar, birçok matematiksel konseptin temelini oluşturur ve birçok uygulama alanında önemli bir rol oynar.
Orantı Nedir?
Orantı, matematikte iki oran arasındaki ilişkiyi ifade eden bir kavramdır. Bir orantıda, iki oran birbirine eşittir. Yani, a/b = c/d şeklindeki ifadede, a/b oranı ile c/d oranı birbirine eşittir.
Matematiksel olarak, a, b, c ve d reel sayılar olmak üzere, b ve c sıfırdan farklıdır. Bu durumda, orantı şu şekilde ifade edilir:
a/b = c/d
Bu ifade, a ile b’nin oranının, c ile d’nin oranına eşit olduğunu belirtir.
Orantılar, birçok matematiksel problemin çözümünde ve gerçek hayatta karşılaşılan durumların modellemesinde kullanılır. Orantılar, benzer üçgenlerin benzer kenar uzunlukları, miktarlar arasındaki ilişkiler, hız ve zaman gibi birçok konseptin anlaşılmasına yardımcı olur.
Doğru Orantı Nedir?
Bir çokluk artıyorken diğer çokluk da aynı oranda artıyorsa veya bir çokluk azalırken diğer çokluk da aynı oranda azalıyorsa bu çokluklara doğru orantı denir. a ve b çoklukları doğru orantılı ise;
k = a/b şeklinde gösterilir.
Doğru Orantılı Çokluklar
Doğru orantılı çokluklar, birbirleriyle doğru orantılı olan birden fazla grup veya küme anlamına gelir. İki oranın eşit olduğu durumu anlamak için önce doğru orantı kavramını hatırlayalım. İki oranın doğru orantılı olması, bu oranların birbirleriyle orantılı olduğu anlamına gelir:
a/b = c/d
Bu ifade, a/b oranının c/d oranına eşit olduğunu gösterir.
Doğru orantılı çokluklar, üç veya daha fazla grup arasında doğru orantı ilişkisinin olduğu durumu ifade eder. Örneğin, üç grup A, B ve C’nin doğru orantılı olduğu bir durumu şu şekilde ifade edebiliriz:
a/b = c/d = e/f
Bu durumda, A ile B’nin oranı, C ile D’nin oranı, ve E ile F’nin oranı birbirine eşittir.
Doğru orantılı çokluklar, benzer üçgenlerin kenar uzunluklarını, oranlara dayalı problemleri ve çeşitli matematiksel modelleri ifade etmek için kullanılır. Bu tür kavramlar, matematikte orantı ve orantılılık konularını anlamak ve uygulamak için önemlidir.
Ters Orantı Nedir?
İki çokluktan biri artarken diğeri aynı oranda azalıyor veya biri azalırken diğer aynı oranda artıyor ise bu çokluklara ters orantı denir.
a ve b çoklukları ters orantılı ise a.b = k şeklinde gösterilir. Bazı kaynaklarda yer alan ters orantı formülü aslında ters orantının a.b = k şekilde gösterimidir.
a ve b değişkenleri arasındaki ters orantı grafikle şekildeki gibi gösterilir.
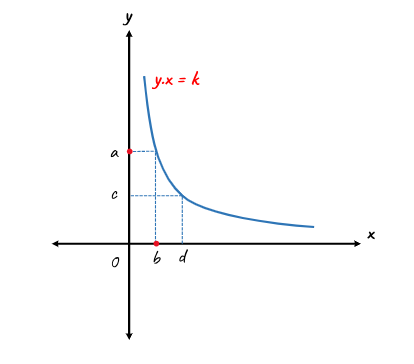
Grafikleri verilen değişkenler ters orantılı oldukları için;
a.b = a.c = k eşitliğini yazabiliriz.
Ters Orantılı Çokluklar
Ters orantılı çokluklar, iki veya daha fazla grup arasında ters orantı ilişkisinin bulunduğu durumu ifade eder. İki niceliğin ters orantılı olduğu bir durumda, bir nicelik artarken diğer nicelik azalır veya tam tersi şekilde, bir nicelik azaldığında diğer nicelik artar.
Matematiksel olarak, iki niceliğin ters orantılı olduğu durumu şu şekilde ifade edebiliriz:
xy=k
Burada, x ve y iki farklı niceliği temsil eder ve k bir sabittir. Bu durumda, x ile y ters orantılıdır, çünkü biri artarken diğeri azalır.
Doğru Orantı ve Ters Orantı Problemleri
Örnek: a,b,c sayıları sırasıyla 2, 5, 7 ile orantılıdır. 2a + 3b + 4c = 94 olduğuna göre a kaçtır?
a,b,c sayıları sırasıyla 2, 5,7 ile orantılı olduğundan
a/2 = b/5 = c/7 = k olur.
Buradan a = 2k, b = 5k, c = 7k dır.
2a + 3b + 4c = 94
2.2k + 3.5k + 4.7k = 94
4k + 15k + 28k = 94
47k = 94
k = 2 dir.
a = 2k = 2.2 = 4 tür.
Örnek: a sayısı ile b sayısı ters orantılıdır. a=9 iken b=4 ise a=12 iken b kaçtır?
a ve b ters orantılı ise a.b = k dir.
a = 9 iken b = 4
a.b = k ⇒ 9.4 = k
36 = k
a = 12 iken b nin değeri ise
a.b = k
12.b = 36
b = 3’tür
Oran – Orantı Özellikleri
- Oranlanan çokluklardan ikisi aynı anda sıfır olamaz.
- Oranın payı ya da paydası sıfır olabilir.
- Oranlanan çoklukların birimleri aynı tür olmalıdır.
- Oranın sonucu birimsizdir.
- Bir orantıda içlerin çarpımı dışların çarpımına eşittir.
- Orantıdaki çapraz terimler aralarında yer değiştirirse oranların eşitliği bozulmaz, ancak oluşan yeni orantının orantı sabiti farklı olur.
- Bir orantıdaki oranların çarpmaya göre tersi alınırsa (pay ve paydasındaki sayılar aralarında yer değiştirirse), orantı sabitinin de çarpmaya göre tersi alınır.
- Bir orantıdaki oranların payları kendi aralarında, paydaları da kendi aralarında toplanırsa ya da çıkarılırsa, orantı sabiti değişmez.
- Aynı işlemi bir orantıdaki oranları belirli sayılarla genişleterek yaparsak da orantı sabiti değişmez.
- Bir orantıdaki belirli sayıda oranın çarpımının oranı, orantı sabitinin aynı sayıda kuvvetine eşittir.
- İki orantılı terimin paylarının ve paydalarının kendi aralarında bölümlerinin oranı bire eşittir.
- Bir orantıdaki oranların belirli bir kuvvetinin oranı, orantı sabitinin aynı sayıda kuvvetine eşittir.
Oranı Verilen İki Çokluktan Biri Verildiğinde Diğerini Bulma
Birbirine oranı verilen iki çokluktan biri verildiğinde diğerini bulmak için verilen orana göre bir eşitlik oluşturulur. Elde edilen eşitlikte oranların birbirinin kaç katı olduğu bulunarak verilmeyen değer bulunur.

