A bike shop uses two manufacturing plants, one in region A

Last updated: 7/24/2022

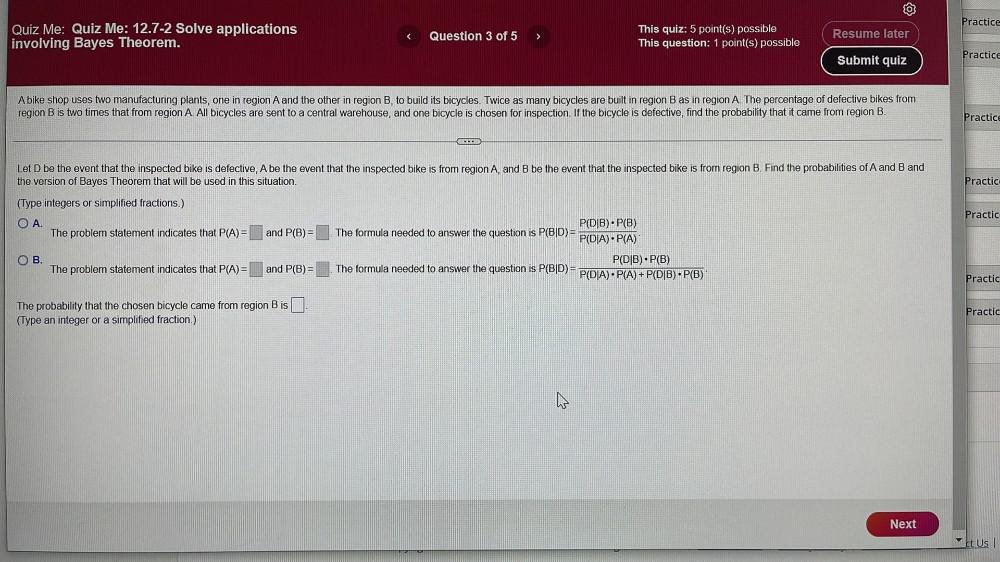
A bike shop uses two manufacturing plants, one in region A and the other in region B, to build its bicycles. Twice as many bicycles are built in region B as in region A. The percentage of defective bikes from region B is two times that from region A. All bicycles are sent to a central warehouse, and one bicycle is chosen for inspection. If the bicycle is defective, find the probability that it came from region B. Let D be the event that the inspected bike is defective, A be the event that the inspected bike is from region A, and B be the event that the inspected bike is from region B. Find the probabilities of A and B and the version of Bayes Theorem that will be used in this situation. A. The problem statement indicates that P(A) = and P(B) = The formula needed to answer the question is P(BID)= P(DIB).P(B) / P(DIA).P(A) B. The problem statement indicates that P(A) = and P(B) = The formula needed to answer the question is P(BID)= P(DIB).P(B) / P(DIA).P(A) + P(DIB).P(B) The probability that the chosen bicycle came from region B is (Type an integer or a simplified fraction.)