b Compute the probability that exactly one of the appeals

Last updated: 12/5/2023

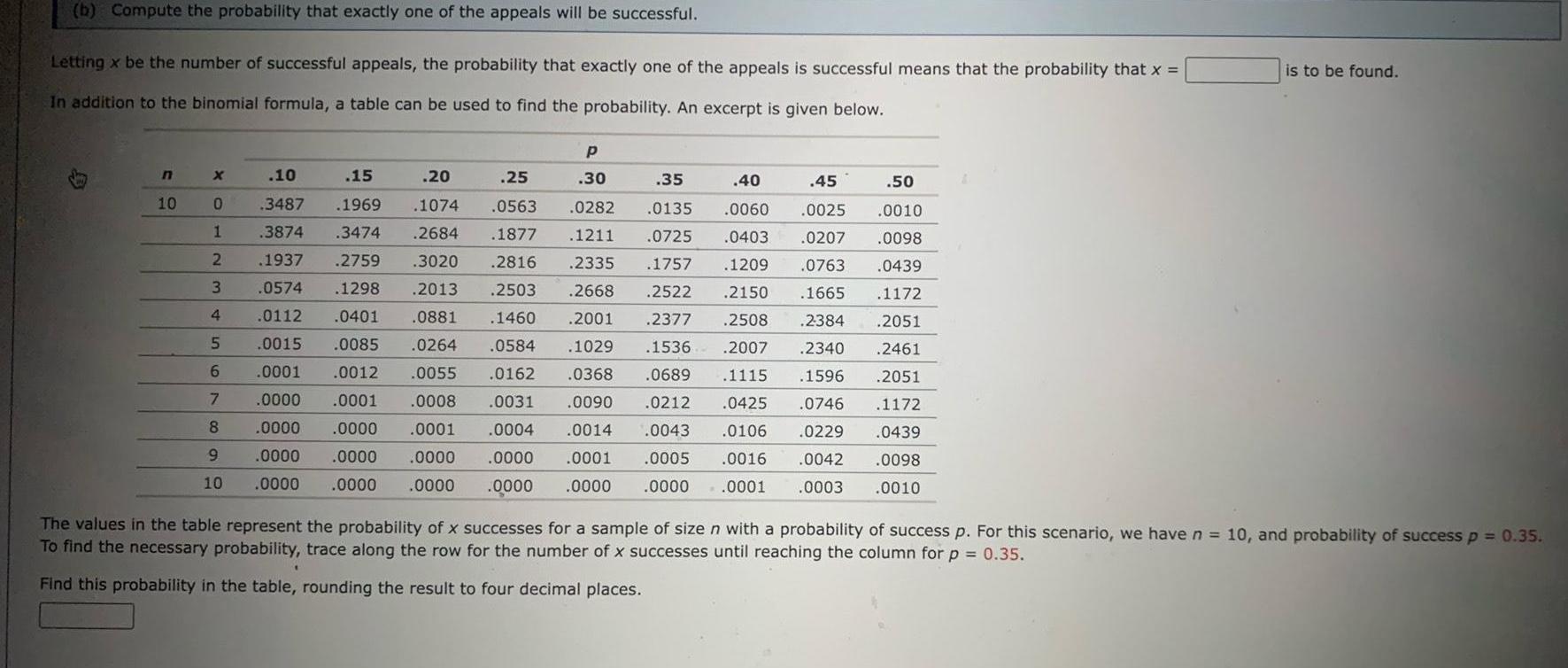
b Compute the probability that exactly one of the appeals will be successful Letting x be the number of successful appeals the probability that exactly one of the appeals is successful means that the probability that x In addition to the binomial formula a table can be used to find the probability An excerpt is given below n 10 P 30 X 10 0 15 20 25 1969 1074 0563 3474 2684 1877 50 0010 3487 35 0282 0135 1211 0725 1 3874 40 45 0060 0025 0403 0207 1209 0763 2150 1665 2 1937 3 0574 4 0112 5 0098 2759 3020 2816 2335 1757 0439 1298 2013 2503 2668 2522 1172 0401 0881 1460 2001 2377 2508 2384 2051 0015 0085 0264 0584 1029 1536 2007 2340 2461 0012 0055 0162 0368 0689 1115 1596 0000 0001 0008 0031 0090 0212 0425 0746 0000 0000 0001 0004 0014 0043 0106 0229 0000 0000 0000 0000 0001 0005 0016 0042 10 0000 0000 0000 0000 0000 0000 0001 6 0001 2051 7 1172 8 0439 9 0098 0003 0010 The values in the table represent the probability of x successes for a sample of size n with a probability of success p For this scenario we have n 10 and probability of success p 0 35 To find the necessary probability trace along the row for the number of x successes until reaching the column for p 0 35 1 is to be found Find this probability in the table rounding the result to four decimal places