By expanding in a Maclaurin series and integrating term by

Last updated: 6/29/2023

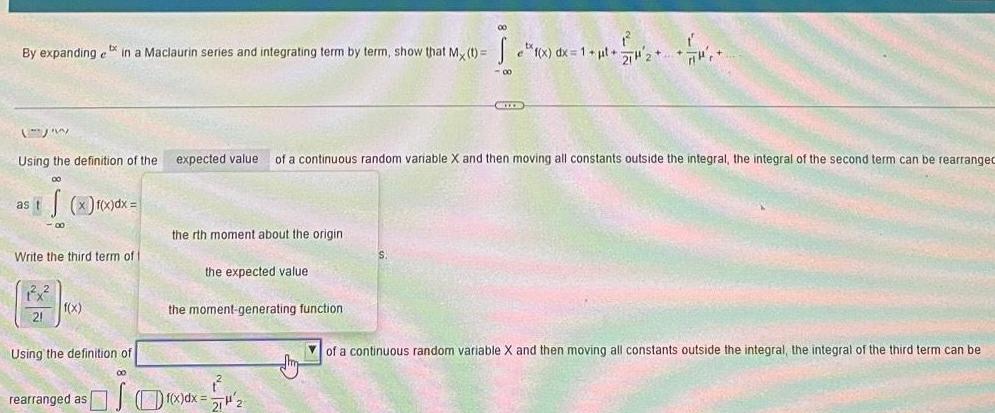
By expanding in a Maclaurin series and integrating term by term show that Mx t 1 x dx 1 t 1 x dx 1 l 2 Write the third term of t 1 x 2 21 3 Using the definition of the expected value of a continuous random variable X and then moving all constants outside the integral the integral of the second term can be rearranged as t f x f x dx f x Using the definition of 80 the rth moment about the origin the expected value 00 the moment generating function rearranged as 1 x dx 2 00 CRECE of a continuous random variable X and then moving all constants outside the integral the integral of the third term can be