Evaluate the polynomial function for x = -6 and x = -3. f(x)

Last updated: 7/16/2022

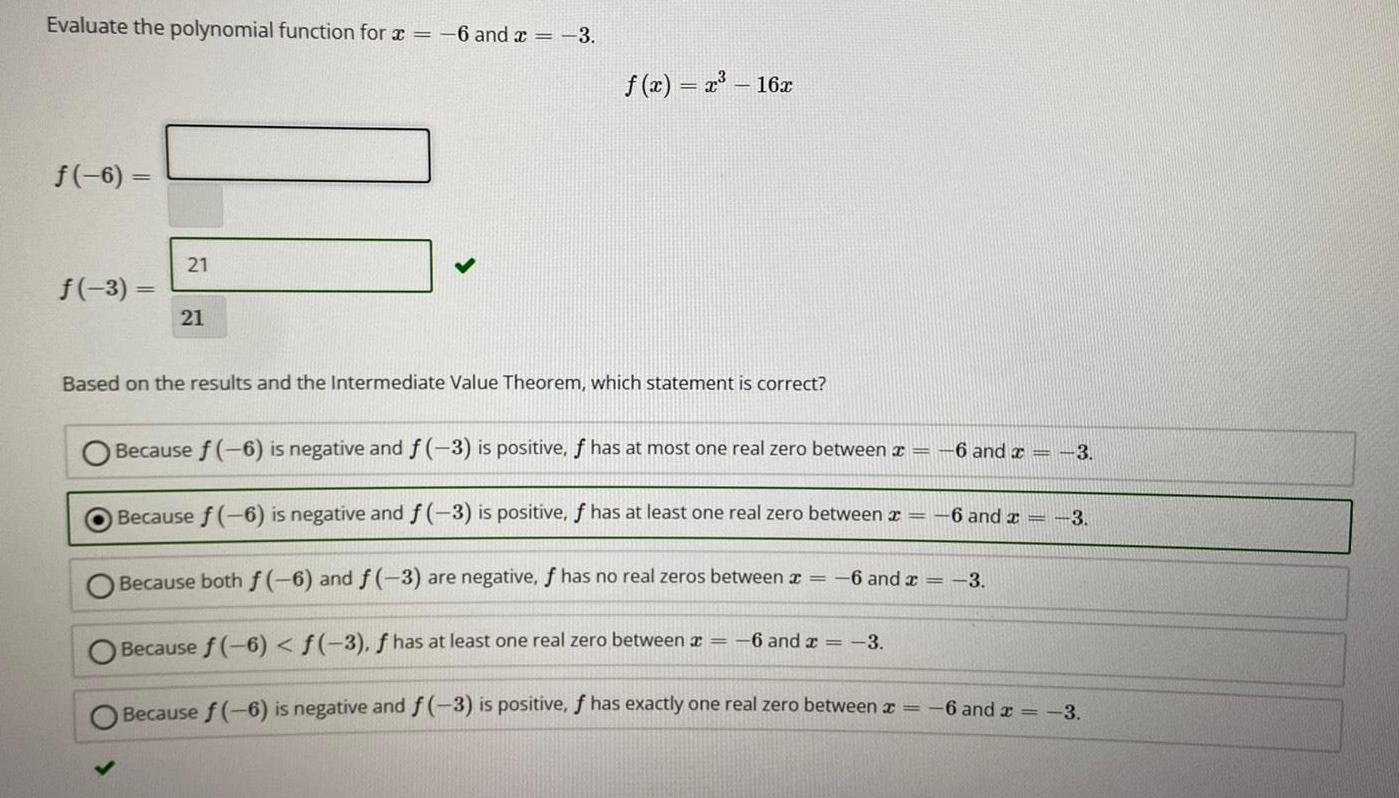
Evaluate the polynomial function for x = -6 and x = -3. f(x) = x³ - 16x f(-6)= f(-3) = Based on the results and the Intermediate Value Theorem, which statement is correct? Because f(-6) is negative and f(-3) is positive, f has at most one real zero between x= -6 and x= -3 Because f(-6) is negative and f(-3) is positive, f has at least one real zero between x = -6 and x= -3 Because both f(-6) and f(-3) are negative, f has no real zeros between x = -6 and x = -3 Because f(-6) < f(-3), f has at least one real zero between x = -6 and x = -3. Because f(-6) is negative and f(-3) is positive, f has exactly one real zero between x = -6 and x = -3.