Find the power series solution of the initial value problem

Last updated: 8/9/2023

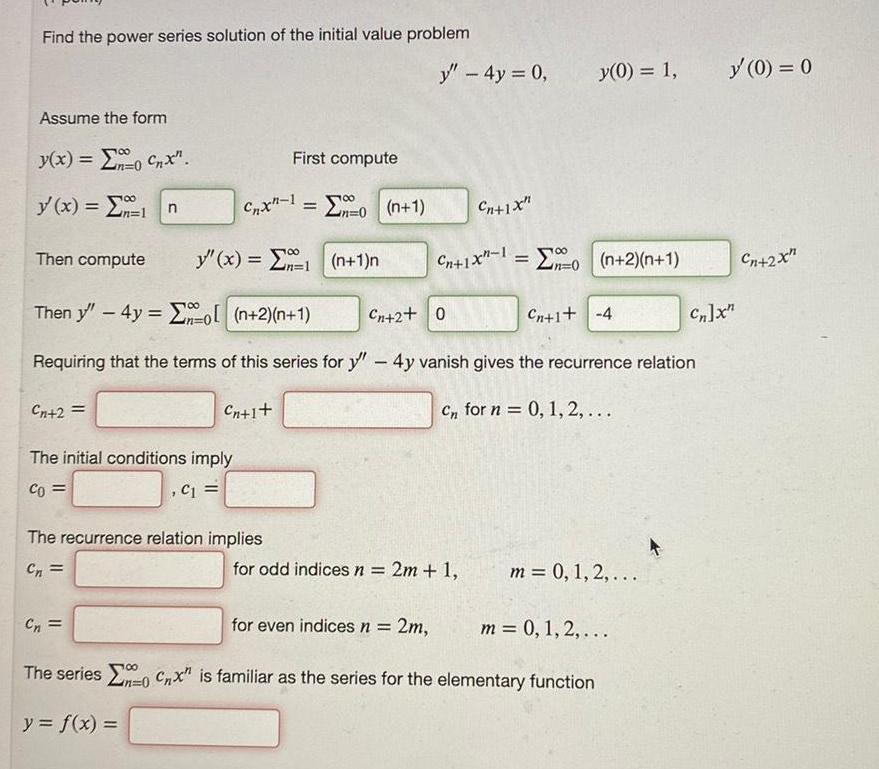
Find the power series solution of the initial value problem Assume the form y x 0 Cnx n 0 y x n 1 Then compute n C x 1 0 Cn First compute y x 1 n 1 n n Cn 1 The recurrence relation implies Cn 0 n 1 y 4y 0 Then y 4y n 2 n 1 Requiring that the terms of this series for y 4y vanish gives the recurrence relation Cn 2 Cn for n 0 1 2 The initial conditions imply Co C for odd indices n Cn 2 0 Cn 1X Cn 1x 1 n 2 n 1 2m 1 y 0 1 Cn 1 4 for even indices n 2m The series 0 Cnx is familiar as the series for the elementary function in 0 y f x m 0 1 2 m 0 1 2 y 0 0 Cn x Cn 2x