Find the sum of the infinite geometric series if possible

Last updated: 11/19/2023

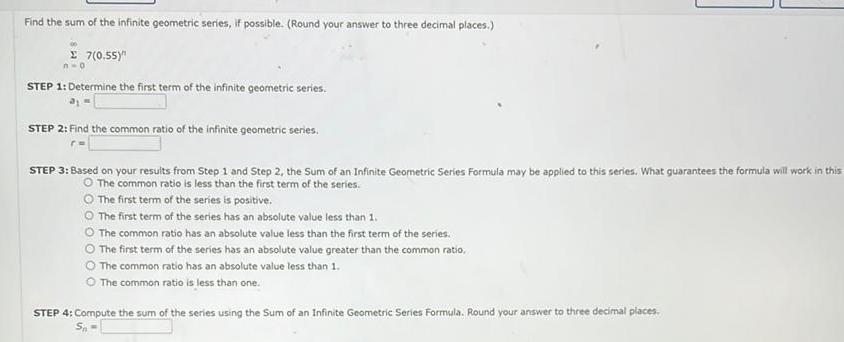
Find the sum of the infinite geometric series if possible Round your answer to three decimal places 7 0 55 STEP 1 Determine the first term of the infinite geometric series n o STEP 2 Find the common ratio of the infinite geometric series STEP 3 Based on your results from Step 1 and Step 2 the Sum of an Infinite Geometric Series Formula may be applied to this series What guarantees the formula will work in this The common ratio is less than the first term of the series The first term of the series is positive The first term of the series has an absolute value less than 1 O The common ratio has an absolute value less than the first term of the series The first term of the series has an absolute value greater than the common ratio The common ratio has an absolute value less than 1 The common ratio is less than one STEP 4 Compute the sum of the series using the Sum of an Infinite Geometric Series Formula Round your answer to three decimal places S