functions Consider the functions fff and f given by the

Last updated: 10/10/2023

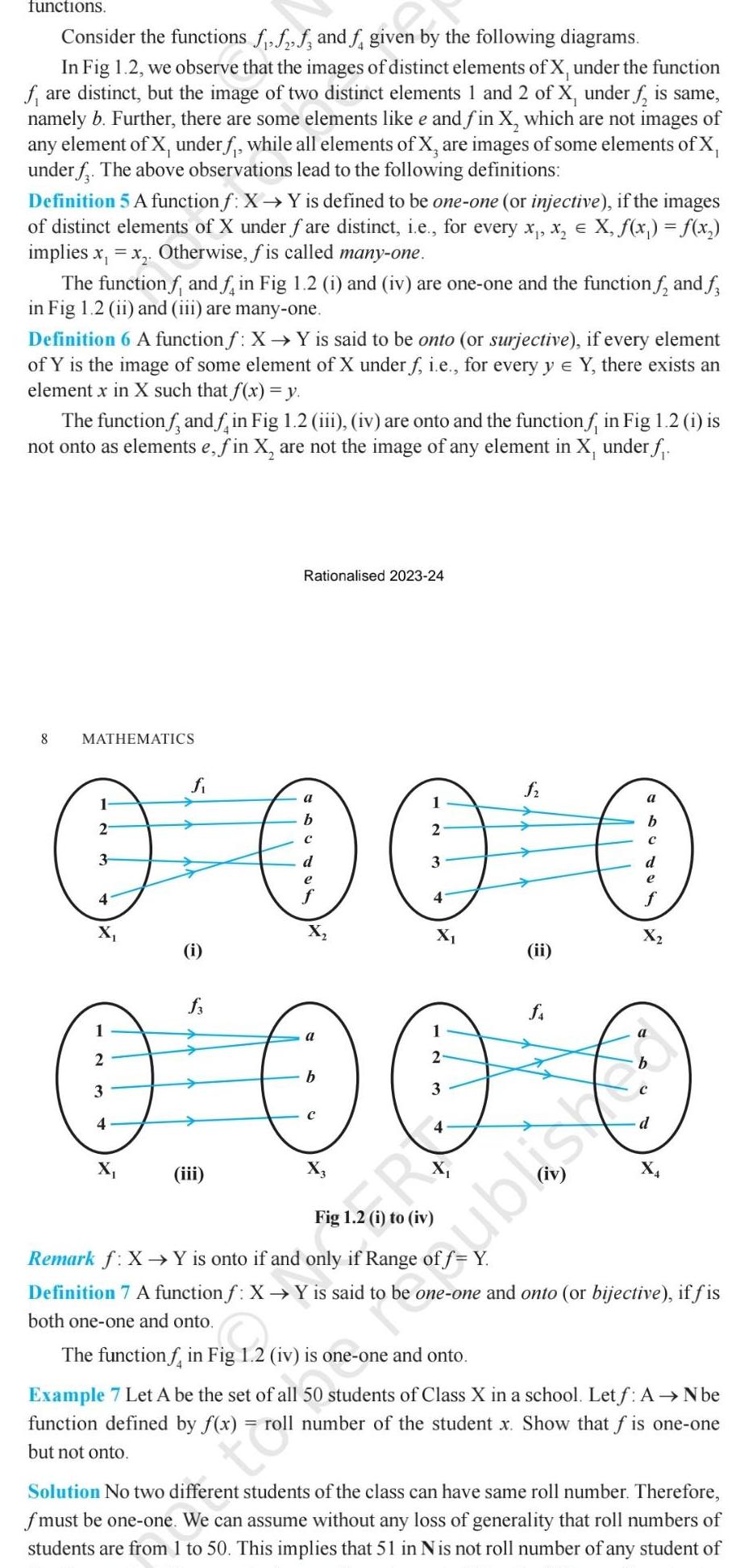
functions Consider the functions fff and f given by the following diagrams In Fig 1 2 we observe that the images of distinct elements of X under the function fare distinct but the image of two distinct elements 1 and 2 of X under f is same namely b Further there are some elements like e and fin X which are not images of any element of X under f while all elements of X are images of some elements of X under f The above observations lead to the following definitions Definition 5 A function f X Y is defined to be one one or injective if the images of distinct elements of X under fare distinct i e for every x x X f x f x implies x x Otherwise fis called many one The function f and f in Fig 1 2 i and iv are one one and the function f and f in Fig 1 2 ii and iii are many one Definition 6 A function f X Y is said to be onto or surjective if every element of Y is the image of some element of X under f i e for every y Y there exists an element x in X such that f x y The function and in Fig 1 2 iii iv are onto and the function f in Fig 1 2 i is not onto as elements e fin X are not the image of any element in X under f 8 MATHEMATICS fi a 1 1 a b 2 2 3 d 3 e e 4 4 X X O O O O 0 0 0 0 a 2 2 b 3 3 4 4 iii Rationalised 2023 24 i ii shari Remark f X Y is onto if and only if Range of f Y Definition 7 A function f X Y is said to be one one and onto or bijective if fis both one one and onto The function f in Fig 1 2 iv is one one and onto Example 7 Let A be the set of all 50 students of Class X in a school Let f A N be function defined by f x roll number of the student x Show that f is one one but not onto troll Solution No two different students of the class can have same roll number Therefore fmust be one one We can assume without any loss of generality that roll numbers of students are from 1 to 50 This implies that 51 in Nis not roll number of any student of