in example 15 2 can you explain last 4 steps of solution
Last updated: 6/26/2023
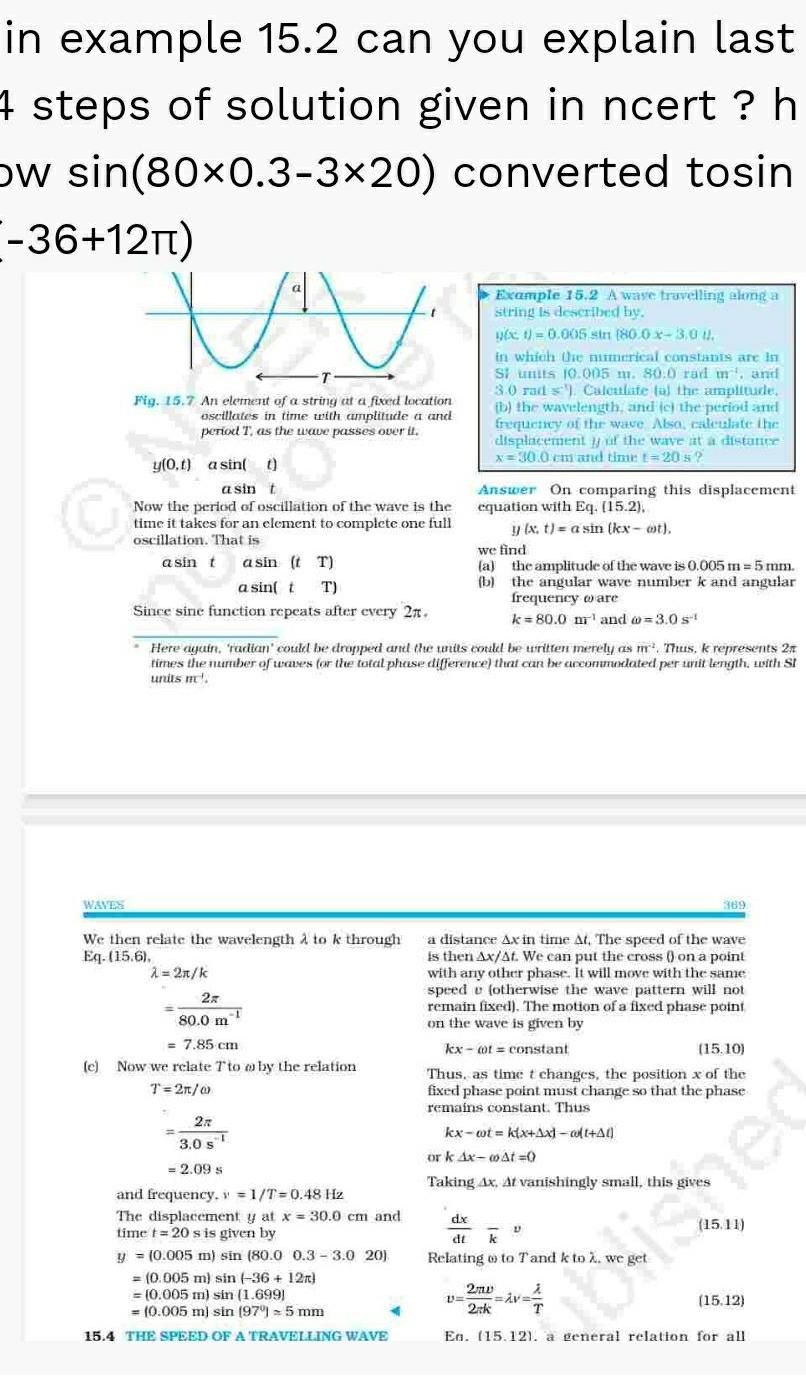
in example 15 2 can you explain last 4 steps of solution given in ncert h ow sin 80x0 3 3x20 converted tosin 36 12 WAVES VV Fig 15 7 An element of a string at a fixed location oscillates in time with amplitude a and period T as the wave passes over it y 0 t a sin a sin t Now the period of oscillation of the wave is the time it takes for an element to complete one full oscillation That is a sin t asin t T a sin t T Since sine function repeats after every 2 We then relate the wavelength to k through Eq 15 6 2n k 2x 80 0 m 7 85 cm c Now we relate Tto by the relation T 2r a 2n 3 0 s 2 09 s and frequency v 1 T 0 48 Hz The displacement y at x 30 0 cm and time t 20 s is given by y 0 005 m sin 80 0 0 3 3 0 20 0 005 m sin 36 12m 0 005 m sin 1 699 0 005 m sin 97 5 mm 15 4 THE SPEED OF A TRAVELLING WAVE Here again radian could be dropped and the units could be written merely as mr Thus k represents 2 times the number of waves for the total phase difference that can be accommodated per unit length with Sl units m Example 15 2 A wave travelling along a string is described by ux 0 005 sin 80 0 x 3 0 U in which the numerical constants are in Si units 10 005 m 80 0 rad m and 3 0 rad s Calculate tal the amplitude b the wavelength and c the period and frequency of the wave Also calculate the displacement of the wave at a distance x 30 0 cm and time t 20 s Answer On comparing this displacement equation with Eq 15 2 y x t a sin kx ot we find a b the amplitude of the wave is 0 005 m 5 mm the angular wave number k and angular frequency o are k 80 0 m and 3 0 s 2mv 2rk V a distance Ax in time At The speed of the wave is then Ax At We can put the cross on a point with any other phase It will move with the same speed otherwise the wave pattern will not remain fixed The motion of a fixed phase point on the wave is given by kx at constant 15 10 Thus as time t changes the position x of the fixed phase point must change so that the phase remains constant Thus kx wot klx Ax 1 Al or k Ax At 0 Taking Ax At vanishingly small this gives dx dt k Relating to Tand k to A 369 D A Av T En 15 12 a general relation for all 15 12