Let F be any field and n be a positive integer. Let M be the

Last updated: 8/7/2022

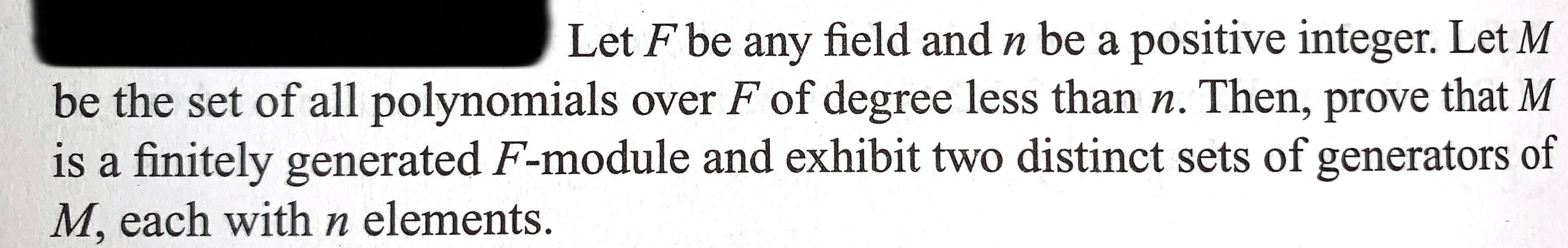
Let F be any field and n be a positive integer. Let M be the set of all polynomials over F of degree less than n. Then, prove that M is a finitely generated F-module and exhibit two distinct sets of generators of M, each with n elements.