position of a point in three dimensional space we have to give three numbers To do this we take three mutually perpendicular

Question

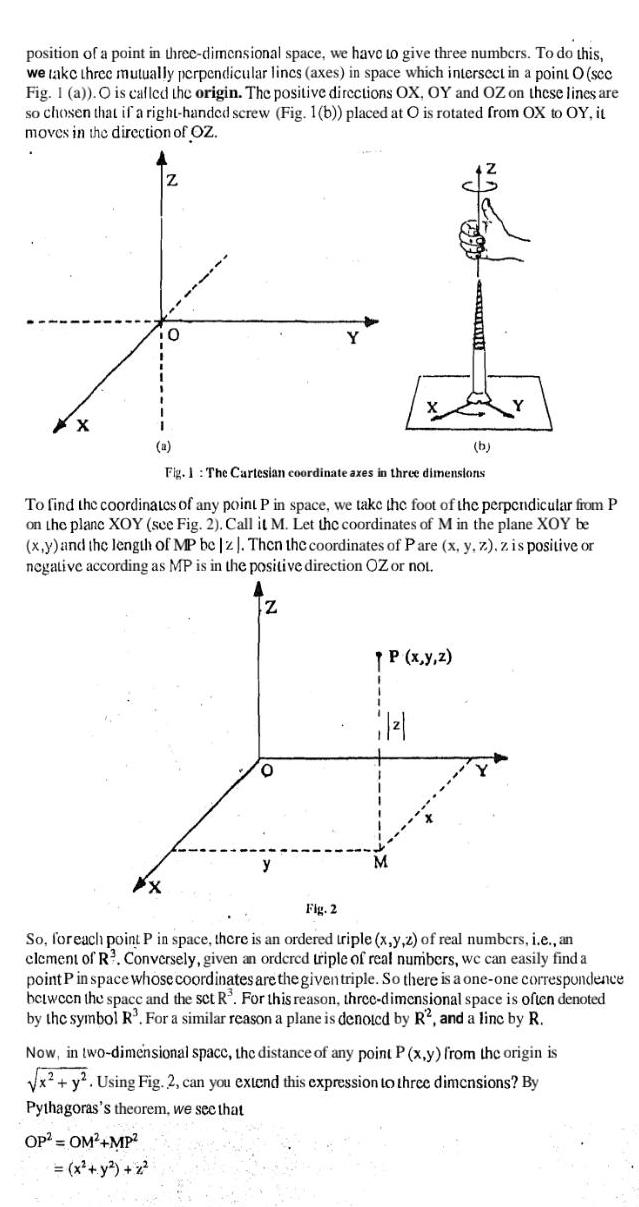
position of a point in three dimensional space we have to give three numbers To do this we take three mutually perpendicular lincs axes in space which intersect in a point O sec Fig 1 a O is called the origin The positive directions OX OY and OZ on these lines are so chosen that if a right handed screw Fig 1 b placed at O is rotated from OX to OY it moves in the direction of OZ XX Z X 0 OP OM MP x y z a Fig 1 The Cartesian coordinate axes in three dimensions To find the coordinates of any point P in space we take the foot of the perpendicular from P on the plane XOY see Fig 2 Call it M Let the coordinates of M in the plane XOY be x y and the length of MP be z Then the coordinates of Pare x y z z is positive or negative according as MP is in the positive direction OZ or not Z O NACE P x y z 662 1 b Fig 2 So for each point P in space there is an ordered triple x y z of real numbers i e an element of R Conversely given an ordcrcd triple of real numbers we can easily find a point P in space whose coordinates are the given triple So there is a one one correspondence between the space and the set R For this reason three dimensional space is often denoted by the symbol R For a similar reason a plane is denoted by R2 and a linc by R Now in two dimensional space the distance of any point P x y from the origin is x y Using Fig 2 can you extend this expression to three dimensions By Pythagoras s theorem we see that

Kunduz · Accepted Answer

Click to see the answer