Step 4 Step 2 To determine the critical numbers of g(x), set

Last updated: 8/13/2022

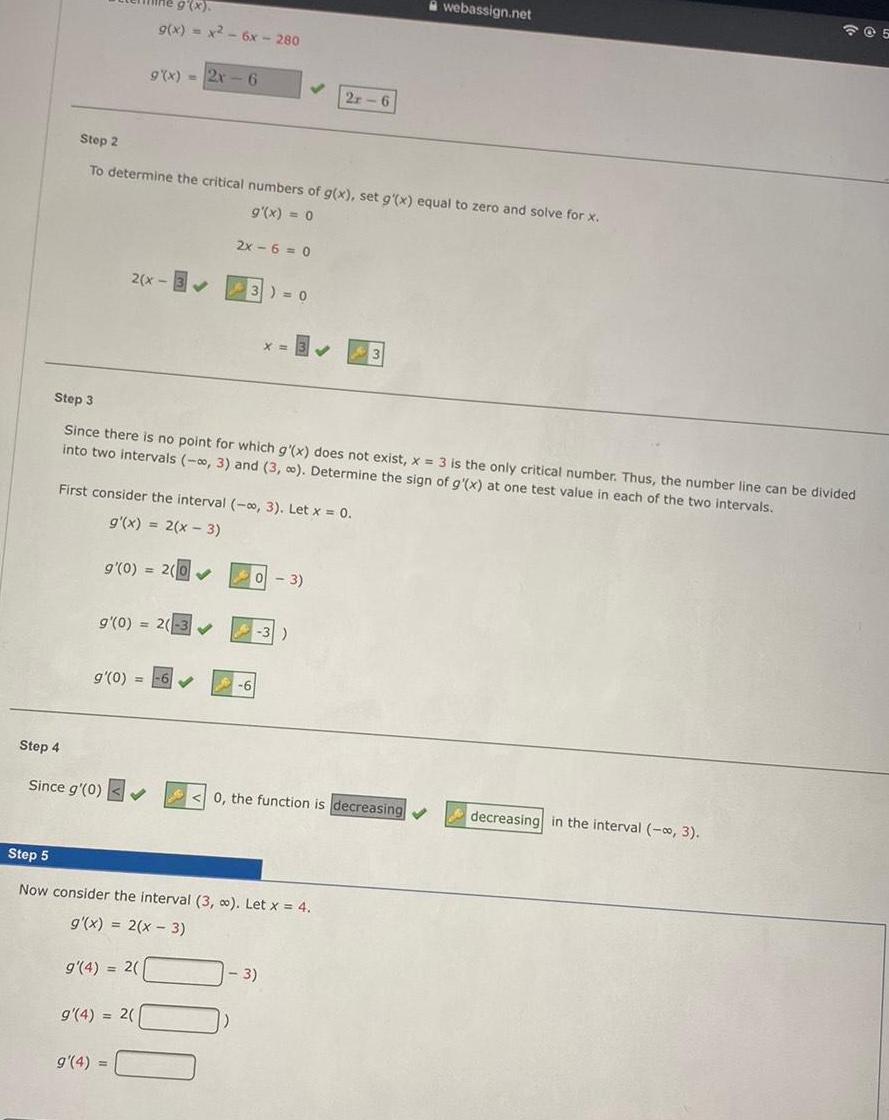
Step 4 Step 2 To determine the critical numbers of g(x), set g'(x) equal to zero and solve for x. g'(x) = 0 g(x). g(x) = x² - 6x - 280 2(x-33) = 0 g'(0) = 9(x)=2x-6 g'(0) = 2(-3✔ Since g'(0) ✓ First consider the interval (-∞, 3). Let x = 0. g'(x) = 2(x-3) 9'(0) = 2(0✔ Step 3 Since there is no point for which g'(x) does not exist, x = 3 is the only critical number. Thus, the number line can be divided into two intervals (-∞, 3) and (3, ∞). Determine the sign of g'(x) at one test value in each of the two intervals. g'(4) = 2( g'(4) = 2( g'(4) = 2x-6=0 ✓ X= Step 5 Now consider the interval (3, ∞). Let x = 4. g'(x) = 2(x - 3) 2r-6 - 3) -3) - 3) 0, the function is decreasing ✔ webassign.net 205 decreasing in the interval (-∞, 3).