Store makes Valentine s Day gift boxes that cost 10 75 and
Last updated: 4/23/2023
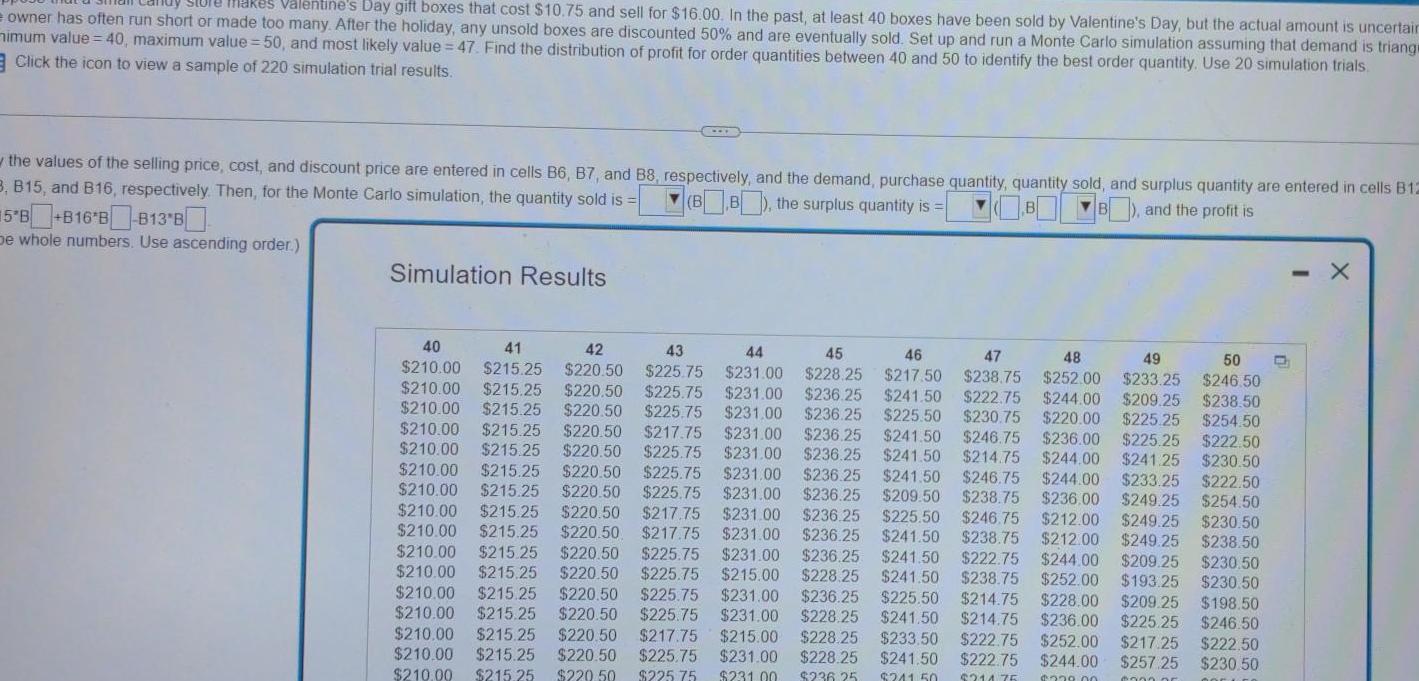
Store makes Valentine s Day gift boxes that cost 10 75 and sell for 16 00 In the past at least 40 boxes have been sold by Valentine s Day but the actual amount is uncertair owner has often run short or made too many After the holiday any unsold boxes are discounted 50 and are eventually sold Set up and run a Monte Carlo simulation assuming that demand is triange nimum value 40 maximum value 50 and most likely value 47 Find the distribution of profit for order quantities between 40 and 50 to identify the best order quantity Use 20 simulation trials Click the icon to view a sample of 220 simulation trial results the values of the selling price cost and discount price are entered in cells B6 B7 and B8 respectively and the demand purchase quantity quantity sold and surplus quantity are entered in cells B12 B B15 and B16 respectively Then for the Monte Carlo simulation the quantity sold is BB the surplus quantity is B B and the profit is 5B B16 B B13 B De whole numbers Use ascending order Simulation Results 43 45 46 47 48 50 40 41 42 44 49 210 00 215 25 220 50 225 75 231 00 228 25 217 50 238 75 252 00 233 25 246 50 210 00 215 25 220 50 225 75 231 00 236 25 241 50 222 75 244 00 209 25 238 50 210 00 215 25 220 50 225 75 231 00 236 25 225 50 230 75 220 00 225 25 254 50 210 00 215 25 220 50 217 75 231 00 236 25 241 50 246 75 236 00 225 25 222 50 210 00 215 25 220 50 225 75 231 00 236 25 241 50 214 75 244 00 241 25 230 50 210 00 215 25 220 50 225 75 231 00 236 25 241 50 246 75 244 00 233 25 222 50 210 00 215 25 220 50 225 75 231 00 236 25 209 50 238 75 236 00 249 25 254 50 210 00 215 25 220 50 217 75 231 00 236 25 225 50 246 75 212 00 249 25 230 50 210 00 215 25 220 50 217 75 231 00 236 25 241 50 238 75 212 00 249 25 238 50 210 00 215 25 220 50 225 75 231 00 236 25 241 50 222 75 244 00 209 25 230 50 210 00 215 25 220 50 225 75 215 00 228 25 241 50 238 75 252 00 193 25 230 50 210 00 215 25 220 50 225 75 231 00 236 25 225 50 214 75 228 00 209 25 198 50 210 00 215 25 220 50 225 75 231 00 228 25 241 50 214 75 236 00 225 25 246 50 210 00 215 25 220 50 217 75 215 00 228 25 233 50 222 75 252 00 217 25 222 50 210 00 215 25 220 50 225 75 231 00 228 25 241 50 222 75 244 00 257 25 230 50 210 00 215 25 220 50 225 75 231 00 214 75 000 LE 4350 00 6300 0r 236 25 241 50 n X